重視考題教學價值，鼓勵學生交流展示
——以2014年湖北襄陽卷第25題解題教學為例

☉江蘇省儀征市香溝中心學校 余飛

重視考題教學價值，鼓勵學生交流展示
——以2014年湖北襄陽卷第25題解題教學為例

☉江蘇省儀征市香溝中心學校 余飛

最近一次數學自習課上有學生問了一道中考題，筆者感覺該題很有探究價值，于是就跟全體學生一起開展多解探究，并反思了問題的深層結構，占去一節課的時間，但大家感覺收獲很大.本文記錄這次習題課上的精彩片斷，并反思考題的教學導向，與同行研討.

一、考題及教學對話

題目（2014年湖北襄陽卷第25題）如圖1，A、P、B、C是⊙O上的四點，∠APC＝∠BPC＝60°，過點A作⊙O的切線交BP的延長線于點D.

（1）求證：△ADP∽△BDA；

（2）試探究線段PA、PB、PC之間的數量關系，并證明你的結論；

（3）若AD＝2，PD＝1，求線段BC的長.

1.第（1）問的思路突破

生1：如圖2，作⊙O的直徑AE，由AE是⊙O的直徑，AD是⊙O的切線，得∠DAE＝∠APE＝90°，于是∠PAD＋∠PAE＝∠PAE＋∠E＝90°，所以∠PAD＝∠E.又∠PBA＝∠E，所以∠PAD＝∠PBA，所以△ADP∽△BDA.

生2：由圓周角定理可以先證出△ABC是等邊三角形.如圖3，作直徑AE，連接BE，得Rt△ABE，由∠2＝∠ACB＝60°，得∠1＝30°，從而∠BAD＝60°＝∠APD.再結合公共角∠D＝∠D，可得△ADP∽△BDA.

生3：如圖4，連接OA、OB，由圓周角和圓心角的關系，有∠3＝2∠ACB＝120°，得∠1＝∠2＝30°，從而∠BAD＝60°＝∠APD，就可以轉到上面生2的思路了.

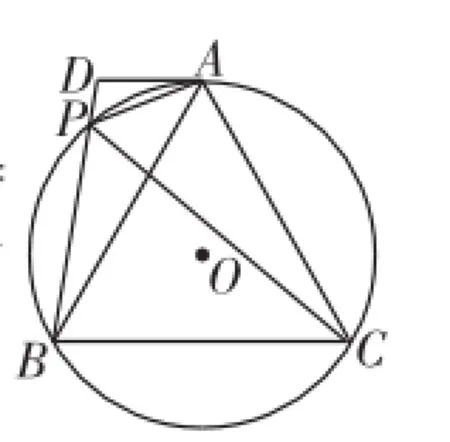
圖1

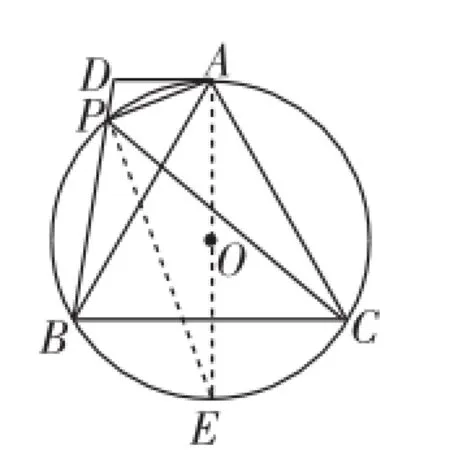
圖2

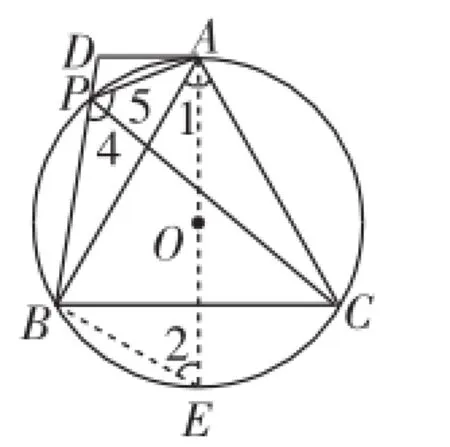
圖3

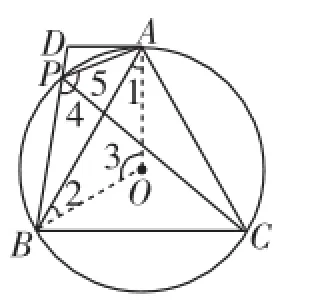
圖4

生4：如圖5，連接OA、OB、OC，證明△OAB≌△OBC，得∠1＝∠2＝30°，從而∠BAD＝60°＝∠APD.

生5：我感覺前面生1的證法中轉了半天得到的“∠PAD＝∠PBA”就是老師以前補充的弦切角性質，是不是可以直接用呢？

師：這個問題提得很好，對這道題來說，建議不能直接使用，因為教材上將弦切角性質定理刪減了，并沒有用“黑體字”形式出現，所以在這道解答題中還是要展示一下推理的過程；當然，如果是填空、選擇或者較復雜的綜合題，也可以作為一種思路啟示直接使用.

2.第（2）問思路突破

生6：可以猜想PA＋PB＝PC.如圖6在線段PC上截取PF＝PB，連接BF，由PF＝PB，∠BPC＝60°，可證得△PBF是等邊三角形，所以PB＝PF，∠BFP＝60°，有∠BFC＝180°-∠PFB＝120°.又因為∠BPA＝∠APC＋∠BPC＝120°，所以∠BPA＝∠BFC.可證△BPA≌△BFC，所以PA＝FC，AB＝BC，所以PA＋PB＝FC＋PF＝PC.

師：很好，看來你的這條輔助線BF起到關鍵的作用，你是怎么想到這條輔助線的呢？

生6：我是想構造出等邊△PBF，再想辦法證△BPA≌△BFC.

生7：如圖7，在PC上截取PG＝PA，連接AG，先證△APG為等邊三角形，再證△APB≌△AGC；或者在PC上截取CG＝PB，連接AG，先證∠ABP＝∠ACG，得△APB≌△AGC，再證△APG為等邊三角形.

生8：如圖8，在PA的延長線上截取AG＝PB（延長PA到點G，使AG＝PB），連接CG，證△ACG≌△BCP，得∠G＝∠4＝60°，再證△CPG為等邊三角形.

圖5

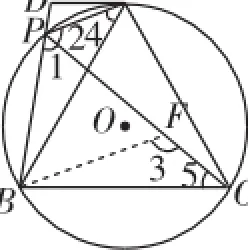
圖6

圖7

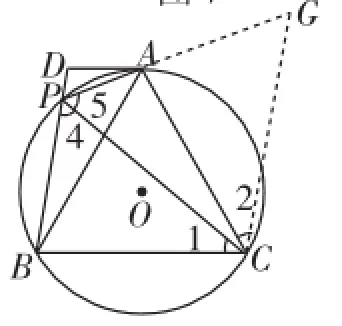
圖8

生9：如圖9，在AP的延長線上截取PH=PB（延長AP到點H，使PH=PB），連接BH，證△ABH≌△CBP，得∠H=∠4=60°，再證△BPH為等邊三角形.

師：看來你們都是充分利用了截長補短策略先構造等邊三角形，再證全等，思路都差不多.大家還可以想想，這道問題的深層結構是什么？跟前面曾經練習過的哪類問題相似？

生10：以前在八年級曾經練習過下面這道問題，如圖10，點D、E分別為等邊△ABC內、外一點，好像能證△ABE≌△CBD，具體條件和要求記不清了.

師：是的，可以從旋轉的角度認識你提到的圖10這個基本問題.對于上面第（2）問的思路確實有啟發作用.

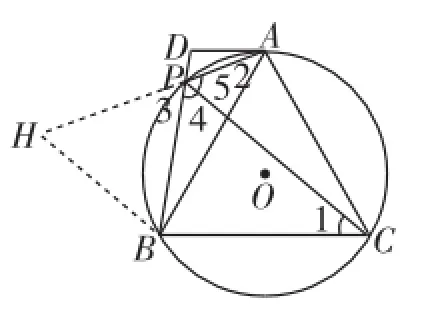
圖9

圖10

3.第（3）問思路突破

師：不錯！這種解法沒有添加輔助線也獲得了思路的貫通，大家覺得思路中的哪個步驟最為關鍵？

生11：發現△ADP∽△CAP，得出AP2=PC·PD.

生12：由（2）中的數量關系“PA+PB=PC”，然后改寫為AP2=（3+AP）·1，這樣就可以利用一元二次方程來求解了.

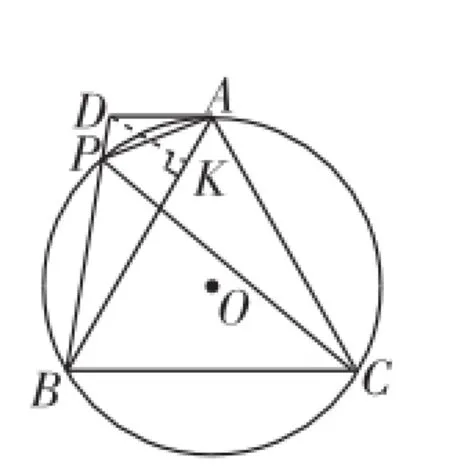
圖11

師：正確.還有不同的思路嗎？

生13：還是要由第（1）問△ADP∽△BDA，求出BD=4.接著如圖11，作DK⊥AB于點K，在Rt△ADK中，由AD=2和∠DAB=60°，求得AK、DK的長，再在Rt△BDK中，由DK、BD求得BK的長，從而BC=AB=AK+BK.

師：很好，這是利用等邊三角形邊長相等，將BC轉化為求AB，然后再把AB用輔助線（高DK）分成兩部分，各個擊破，這個思路能夠啟發其他同學嗎？

生14：如圖12，作DM⊥AP于點M，在Rt△PDM中，由PD=1和∠DPM=60°，求得PM、DM的長，再在Rt△ADM中，由DM、AD求得AM的長，從而AP=AM+ PM；由第（1）問△ADP∽△BDA，可求得AB的長，即得BC的長.

師：很好，你的這種思路利用了切線、垂徑定理，構造出矩形，雖然輔助線多了些，但都是基于特殊圖形而思考，也是很自然的，值得學習.

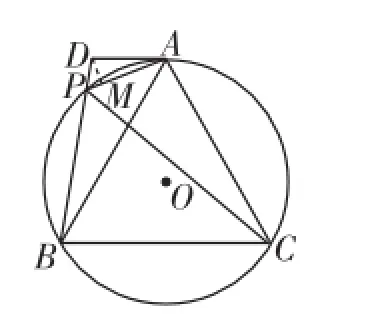
圖12

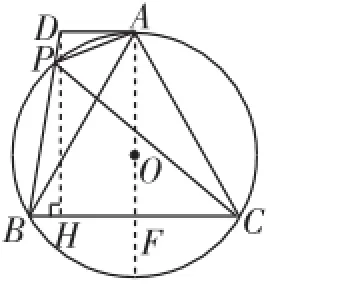
圖13

二、教后反思

一次自習課卻被一道習題占去一節課，但是很多學生在課后的反思寫作中對這節課都很有體會，表達了對這道題的深刻認識.作為教者，這節課除了梳理學生上述的多解以外，還深入思考了命題研究、解題教學等問題，下面展開闡釋.

1.好的試題往往入口較寬，滿足不同思維特點的考生

人民教育出版社中學數學室資深編審章建躍教授在文1中指出：“好的題目應該滿足一些基本條件，例如：反映數學本質，與重要的數學概念和性質相關，不糾纏于細枝末節，體現基礎知識的聯系性，解題方法自然、多樣，具有發展性，表述形式簡潔、流暢且好懂等.”從這個角度來看，上文中的這道考題關注于幾何圖形中重要的數學概念和性質，體現基礎知識之間的關聯，特別是解題方法自然、多樣，是一道很好的試題.這里也可順便提及德國Rita Borromeo Ferri“關于數學思維風格的理論及其實證研究”表明：“那些和教師擁有不同數學思維風格的學生可能在理解方面有一定的問題，如果教師能夠意識到這點，并對數學事實運算不同的方式進行講解，這類問題將會避免.”［2］從上面的課堂實錄看出，不同思維特點的學生有不同的解法出現，比如在第（2）問的求解中，生6~生9思路雖然差不多，但是反映了他們著眼點的不同，有人是著眼于圖形內部構造等邊三角形，有人是著眼于向外構造.

2.選用考題開展解題教學，需要鼓勵學生有不同解法

一般來說，選用中考試題開展解題教學是很多教師經常開展的，問題是如何把這些考題的價值得到充分的發揮，追求“入寶山不空返”是值得認真思考的.從上文的解題教學實錄來看，當我們放手讓學生思考、表達或展示時，學生往往有自己的精彩觀點或思路.從上面對話中，生10基于圖10獲得的破題念頭就是很好的解題經驗分享，一方面他本人獲得問題的思路，另一方面這種破題的心得也通過對話傳遞給其他學生.而在第（3）問的思路突破中，生11沒有構造輔助線也實現了問題的突破，而其他學生的輔助線都不一樣，最后一個學生雖然輔助線用得多了些，但是基于常見圖形的啟發，也是值得鼓勵的.這也是筆者最后在點評時特別強調的.

3.對考題的進一步變式思考

章建躍教授在文1中還曾指出：“解題目的應聚焦于加深理解和掌握雙基；學會思考，培養和發展思維能力；查漏補缺；培養良好的學習習慣；培養創造力等.”而這些目標的實現，根本上還要依靠“好題”.這里，“好題”絕不是當前教輔資源中盛行的那種人為制造的“題目”，而應該是“真正的數學題”.以下我們接著對上文這道考題再做一些發展性的改編，供研討.

改編題如圖14，⊙O是等邊三角形ABC的外接圓，點P是上一點，連接AP，CP，作射線BP.

（1）求證：PC平分∠APB.

（2）試探究線段PA、PB、PC之間的數量關系，并證明你的結論.

（3）過點A作⊙O的切線交射線BP于點D.若AD＝2，PD＝1，求⊙O的半徑.

命題說明：這樣前兩問的圖形更為簡潔，而且是逐次展開、自然生長，由圓周角性質可證第（1）問，繼續思考第（2）問時由上面獲得60°的啟發，也有助于分析思路；到第（3）問整合了原考題的第（1）、（3）問，避免了原來第（1）、（3）問之間的關聯被第（2）問所隔斷的不足.

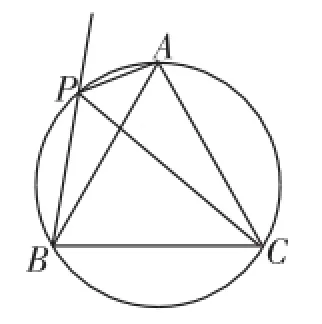
圖14

1.章建躍.發揮數學的內在力量，為學生謀取長期利益［J］.數學通報，2013（2）.

2.［德］Rita Borromeo Ferri.關于數學思維風格的理論及其實證研究［J］.數學教學，2011（3）.W