一道填空題的高失分率引發的思考

☉江蘇省如皋市搬經鎮高明學校 孫小星

一道填空題的高失分率引發的思考

☉江蘇省如皋市搬經鎮高明學校 孫小星

在筆者所在學校八年級數學期中測試的試卷上有一道填空題，試題難度中等，主要考查學生對數形結合思想和分類討論思想的運用能力.應該說本題八年級的學生基本都會做，但結果卻出乎我們的預料，本題全班的實際得分率不足10%，幾乎所有錯誤的答案都是漏解，只考慮了銳角三角形的情況，而沒有考慮鈍角三角形腰上的高在三角形的外部的情況.為了弄清失分原因，筆者對學生進行了調查，并將調查結果進行分析和歸納，由此進行一些反思.

題目：等腰三角形一腰上的高與另一腰的夾角為40°，則該等腰三角形的底角的度數為_________.

一、失分原因

1.受思維定勢的影響

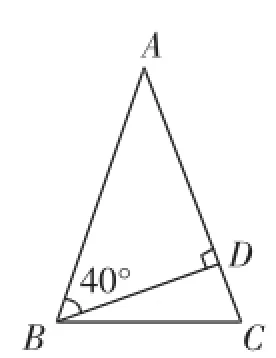
圖1

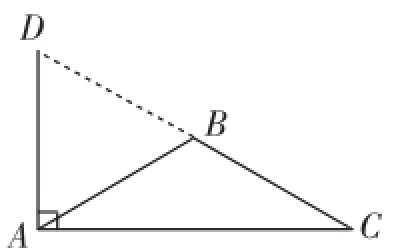
圖2

定勢是指重復先前的心理操作所引起的對活動的準備狀態，它對解題的影響有積極的也有消極的.失分的同學中有近80%是受到了定勢的影響.由于筆者平常在黑板上畫等腰三角形時習慣于畫成銳角的等腰三角形，所以受教師的影響，學生在畫等腰三角形時也習慣于畫出銳角的等腰三角形，長此以往，就形成了畫圖的定勢，所以只畫出了如圖1所示的情況.

2.畫圖基本功不扎實

還有一小部分同學想到了高還可以在三角形的外部的情況，但是筆者在教學過程中過度關注了學生的計算與推理證明的能力，忽視了對學生的畫圖能力的培養，除了書本上必要的作圖內容，其他要求學生畫圖的習題較少，由于缺乏必要的練習，所以學生畫圖的基本功不扎實，從而導致圖形畫不出來，出現了畫圖的典型錯誤，如圖2所示.

3.分類討論的意識不夠

對于題目中沒有給出圖形的幾何題，通常要自己畫圖，而對這類沒有提供圖形的題目在多數情況下都要分類討論.學生平常在練習中完成單解的情況占多數，所以分類討論的意識不強.

二、教學反思與改進措施

結合上述問題，筆者做了深刻的分析，感觸頗深，現將感受總結如下.

1.讓學生認識到畫圖的重要性

初中階段是學生的形象思維能力向抽象思維能力發展過渡的重要時期，但學生的抽象思維能力的發展還是不夠成熟，所以借助于畫圖能夠讓學生理解得更深刻，能幫助學生進一步提高分析問題和解決問題的能力.要使學生體會到畫圖的價值和作用，教學時教師應把握好引導的時機，當學生一時不能解決問題時，不要急于去講解，而是要引導其通過畫圖整理信息、理解題意、找到方法、解決問題.

例1某商業集團新進了40臺空調機和60臺電冰箱，計劃調配給下屬的甲、乙兩個連鎖店銷售，其中70臺給甲連鎖店，30臺給乙連鎖店.兩個連鎖店銷售這兩種電器每臺的利潤（元）如下表所示.

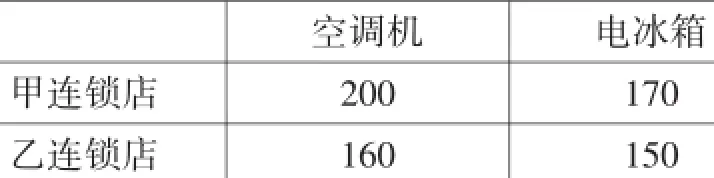
空調機電冰箱甲連鎖店200170乙連鎖店160150

設集團調配給甲連鎖店x臺空調機，集團賣出這100臺電器的總利潤為y（元）.求y關于x的函數關系式，并求出x的取值范圍.

分析：對剛剛接觸一次函數的學生來說，解決本題有一定的困難.由于涉及的條件比較多，好多同學不知所措，這時，教師千萬不要急于講解，否則學生不能學會分析解決此類問題的方法，下次碰到類似的習題還是不會.這時教師要引導學生仿照題目給出的表格自己列出分析表格，如下表所示.（k＜0）的圖像經過點A（1，a）、B（3，b）、C（-2，c），試比較a、b、c的大小.

空調機（總數40臺）電冰箱（總數60臺）甲連鎖店（共需70臺）x70-x乙連鎖店（共需30臺）40-xx-10

分析：由于本題中k的確切的值未知，所以通過代入計算比較a、b、c的大小的方法不可取，而本題中的三個點又不在同一象限，所以不通過畫圖想要來比較它們的大小是比較困難的.通過畫草圖（如圖3），我們很容易比較a、b、c的大小.

3.強化學生的分類討論思想

分類討論思想是初中數學教學中最重要的思想之一.需要運用分類討論思想解決的數學問題有很多，概括起來有以下幾類.

（1）與數學概念有關的分類討論.

例3一個等腰三角形的一個內角為70°，則它一腰上的高與底邊所夾的角的度數為_________.

分析：從等腰三角形的內角這一概念，就要想到分為頂角和底角，因此，就要分兩類來畫圖.（1）當頂角為70°時，畫圖解答；（2）當底角為70°時，畫圖解答.

（2）與公式有關的分類討論.

例4若多項式4x2-kxy+16y2是一個完全平方式，則k=_________.

本題的分類討論源于完全平方公式有兩個：a2± 2ab+b2=（a±b）2，所以-kxy=±16xy?k=±16.

通過完成表格，學生基本可以順利解題.同時，通過此題的解答，幫助學生小結遇到條件比較多的應用題時不要憑空想象，要通過畫圖表來幫助自己分析題意、理解題意.

2.加強對學生的畫圖訓練

在設計練習題時，不能僅設計有圖形的習題，要提高學生的數形結合能力，不僅要培養學生的讀圖能力，更要培養學生自己畫圖的能力.畫圖不僅在幾何題中用到，在代數的函數部分同樣用到的很多.

例2已知反比例函數y=

圖3

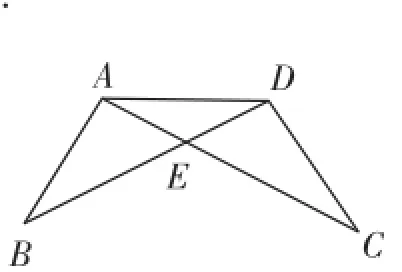
圖4

（3）由運動問題引起的分類討論.

例5在△ABC中，AB=AC，點O是線段BC上的任意一點，OE、OF分別與AB、AC所在的直線垂直，過點B作BG⊥AC，垂足為G.

（1）猜想并證明OE+OF與BG的數量關系.

（2）若點O是直線BC上的任意一點，（1）中的猜想還成立嗎？如果成立，請證明你的猜想；如果不成立，請說明理由.

本題的第二問既考查分類討論思想的運用，又考查學生的畫圖能力，是一道較好的綜合題.

（4）由條件的不確定引起的分類討論.

分類討論的過程，可培養學生思考的嚴謹性、條理性，能促進學生的思維品質的提升.

例6在一次數學課上，王老師在黑板上畫出一幅圖（如圖4），并寫下了四個等式：

①AB=DC；②BE=CE；③∠B=∠C；④∠BAE=∠CDE.

（1）上述四個條件中，由哪兩個條件可以判定△AED是等腰三角形？（用序號寫出所有成立的情形）

（2）請選擇（1）中的一種情形，寫出證明過程.

分析：解決本題首先要分類討論兩兩組合有哪些可能，分別是①②、①③、①④、②③、②④、③④，然后分別判斷它們的正確性.

4.歸納整理易錯題，構建知識網絡

我們經常會碰到這樣一種情況，有些習題反復講解過很多遍，但只要將題目稍作修改，學生便束手無策，究其原因，是學生沒有將知識整理歸納形成網絡，一個不善于歸納總結的學生，他在課堂上只能學到知識，不能形成知識的遷移能力.這樣只能培養出死學習的書呆子，不能使學生成為有創意的人.

作為數學教師，隨時都會碰到學生做錯的習題，對于錯誤率很高的習題要多留心，找出學生出錯的原因，反思自己的教學過程，適時調整自己的教學方向，這樣才能提高教學質量.

1.沈燦江.對一道試題失分的歸因和反思［J］.中國數學教育，2010（4）.

2.莘義成.對一道中考試題失分的思考［J］.中國數學教育，2014（3）.

3.喻瑩瑩.基于幾何復習課的研究［J］.中國數學教育，2014（7）.WG