一次市級數學優質課競賽的亮點展示與思考*

☉甘肅省金昌市第四中學 郭曉梅 馬靜

一次市級數學優質課競賽的亮點展示與思考*

☉甘肅省金昌市第四中學 郭曉梅 馬靜

一、問題提出

甘肅省金昌市教育局在2014年9月23-24日舉辦了兩年一屆的全市優質課競賽教學活動，通過“同課異構”的比較與反思，探討課堂教學的高效性.來自全市各個學校的十三位數學參賽教師中，三位進行了人教版數學七年級上冊“15.1乘方（1）”的授課，三位進行了“15.1乘方（2）”的授課，三位進行了人教版數學八年級上冊“14.2乘法公式（1）”的授課，四位進行了“14.2乘法公式（2）”的授課.本文將本次競賽中的亮點教學設計進行展示，與同行交流.

二、部分參賽者的設計展示

在本次競賽中，各位參賽教師緊緊圍繞新課程理念，解讀教材，分析學情，采用“低起點，小步子，把簡單內容教得豐厚”的設計原則，利用學案導學，從學生最熟悉的問題出發，大膽創新，獨特構思，設計了新穎、活潑的學生活動，充分展現了參賽選手的個人教學風格和魅力.

1.具有代表性的情景設計

（1）乘法公式—平方差公式.

從前有一個狡猾的地主，他把一塊邊長為x米的正方形的土地租給張老漢種植，有一天，他對張老漢說：“我把這塊地的一邊減少5米，另一邊增加5米，繼續租給你，你也沒有吃虧，你看如何？”聰明的同學們，你覺得這個買賣公平嗎？

點評：通過有趣的故事情境引出新課，將學生的數學思維內化為對數學獨特的理解，從而調動了學生的學習積極性，讓學生從中體會數形結合的思想方法在解決數學問題中的應用.

（2）有理數的乘方.

手工拉面是我國的傳統面食.制作時，拉面師傅將一團和好的面揉搓成1根長條后，手握兩端用力拉長，然后將長條對折，再拉長，再對折，每次對折稱為一扣，如此反復操作，連續扣六七次后便成了許多細細的面條.假如拉扣了6次，你能算出共有多少根面條嗎？

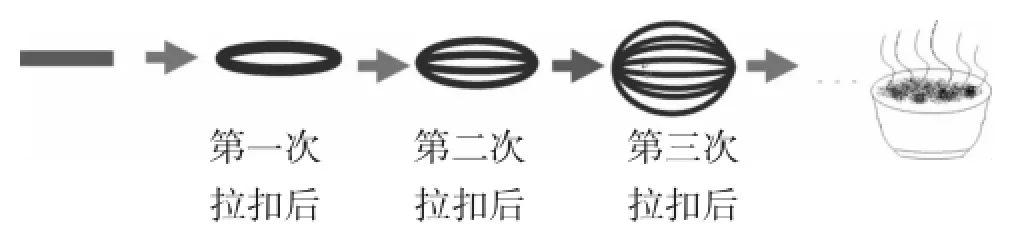
圖1

點評：數學源于生活，又服務于生活，再一次給學生傳達一個信息：學習數學是為了解決發生在我們身邊的問題.

2.具有代表性的學生活動設計

（1）完全平方公式的幾何意義.

活動1：老李有一塊邊長為a米的正方形試驗田.因需要將邊長增加b米，使其變成一個大的正方形試驗田.

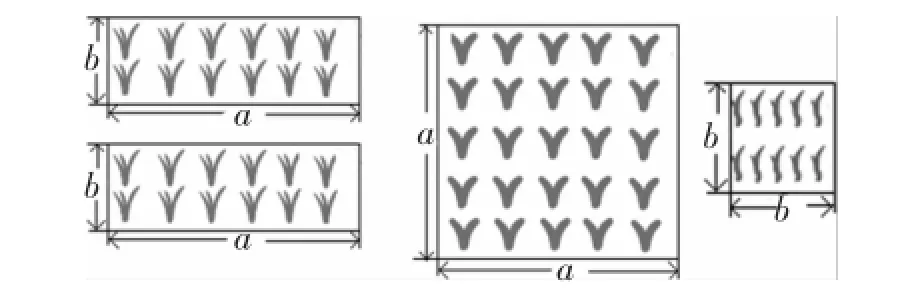
圖2

①請用手中的卡片（如圖2）拼出變化后的試驗田.

②請用不同的方法表示變化后的試驗田的總面積，并進行比較，你能得到什么結論？

活動2：老王有一塊邊長為a米的正方形試驗田.因需要將邊長減少b米，使其變成一個小的正方形試驗田.

①請用手中的卡片（如圖2）拼出變化后的試驗田.

②請用不同的方法表示變化后的試驗田的總面積，并進行比較，你能得到什么結論？

點評：通過學生親自動手拼圖、展示，將數學變成學生看得見、摸得著、理解得了的數學事實，使每一位學生都感受完全平方公式的幾何背景，看清完全平方公式的特征，加深學生對公式理解的深度.

（2）完全平方公式的運用.

請每位同學出一道要求運用完全平方公式來解的計算題，然后同桌交換互測.

點評：讓學生在熟悉完全平方公式的同時，真正成為學習主體，擁有學習主動權，強化主人翁意識.

（3）有理數的乘方（1）.

活動1：請同學們把一張長方形的紙多次對折，所產生的紙的層數和對折的次數有關系嗎？

對折次數1次2次3次4次5次…紙的層數…層數可表示為…

如果對折n次，那么紙的層數是_____.

點評：有效的數學學習活動不能單純地依賴模仿與記憶，需要動手實踐，讓學生在實踐中獲得新知.

點評：通過有趣的故事情境討論，讓學生感受由特殊到一般，以及類比的數學思想方法.

（4）有理數的乘方（2）.有理數的運算王國.

圖3

點評：利用生動的、學生熟悉和感興趣的動畫，展示有理數的混合運算法則，既形象又直觀，也符合學生的認知特點，易于學生掌握，讓學生在學習中留下一個印象深刻的學習故事.

3.具有代表性的德育設計

（1）有理數的乘方（1）.

結束語：“乘方”精神，雖然只是簡簡單單的重復，但結果卻是驚人的.做人和學習也要這樣，腳踏實地，一步一個腳印，成功也會令你驚喜無比.

點評：在數學教學中滲透德育，讓學生先做人，再做學問，起到了很好的教育作用.

（2）完全平方公式.

一位老人非常喜歡孩子.每當有孩子到他家做客時，老人都要拿出糖果招待他們.來一個孩子，老人就給這個孩子一塊糖，來兩個孩子，老人就給每個孩子兩塊塘，….

（1）第一天有a個男孩去了老人家，老人一共給了這些孩子多少塊糖？

（2）第二天有b個女孩去了老人家，老人一共給了這些孩子多少塊糖？

（3）第三天這（a+b）個孩子一起去看老人，老人一共給了這些孩子多少塊糖？

（4）這些孩子第三天得到的糖果數與前兩天他們得到的糖果總數哪個多？多多少？

點評：學生通過計算知道第三天多，多（a+b）2-（a2+ b2）=2ab，教師引導學生明白：數學學習不夠好，生活中不經意間我們就會吃虧.

三、幾點思考

從本次課堂教學競賽可以看出：以學案為載體，學生自主、合作探究為主旨的教學改革試驗在金昌市得到廣泛的肯定與推進，但也有一些問題讓人深思.

1.關于導學案設計意圖的思考

參與本次競賽的十三位教師中，有十二位教師在教學中使用了導學案，但導學案的設計卻迥然不同.在評課環節中，評委對導學案的使用效果提出疑問：在導學案的設計中如何體現導學、導思、導練的功能？導學案實際上是“給學生一個拐杖，讓學生嘗試自學”.學什么，如何學，學到什么程度，在“導學案”中都應該有表述.實際上，導學案的設計上偏重于學習環節的展示和練習題、當堂檢測題的使用，忽視了導學案的導學、導思、導練.

另外，在導學案的實施過程中，的確讓學生自主學習，給了不同層次的學生很多發展空間，但對學習困難的學生來說，這無疑是“雪上加霜”，即使是老師細致的講解都未必能使他們知道知識的來龍去脈，更不用說自主學習了，展示交流就更談不上了，這使得整個班級學習兩極分化嚴重.怎樣才能兩頭兼顧，有待于探求更好的方法.

2.關于教材編寫意圖的思考

有理數的乘方（2）中的例4如下所示.

①-24-816-3264…

②06-618-3066…

③-12-48-1632…

（1）①中的數按什么規律排列？

（2）②③中的數與①中的數分別有什么關系？

（3）取每行數的第10個數，用算式表示這三個數的和.

第三問的分析中，最后計算算式為：（-2）10+［（-2）10+ 2］+［-（-2）9］，在計算結果時，三位參賽教師都讓學生筆算結果，但在評課中，評委認為：在講解例4之前學習了計算器的使用，這道題此處的編寫本意應該是讓學生嘗試使用計算器，無疑評委是正確的.

八年級教材中，完全平方公式的課后練習第2題是按如下方式編寫的.

下面各式的計算錯在哪里？應當怎樣改正？

（1）（a+b）2=a2+b2；

（2）（a-b）2=a2-b2.

在競賽中有兩位老師設計了相應的糾錯練習，實際上在這兩位老師的授課過程中，并無學生出現類似的錯誤，那么這一環節的設計就值得深思.評委認為：當學生出現類似的錯誤時再加以糾錯，效果會更好，而不是為了教學環節，為糾錯而糾錯.

3.關于學習目標展示的思考

參與本次競賽的十三位教師中，有十位教師在教學過程中展示了學習目標.可以看出，展示的學習目標不是簡單的照搬課程標準中規定的學習要求，而是要求非常清楚，具體地寫明要學習什么內容，要達到什么程度，重點和難點是什么，即確定教學或學習的主題.在評課中，評委對學習目標的展示效果提出質疑：課前展示學習目標對學生本節課的學習究竟有沒有幫助？

答案是肯定的，凡事預則立，不預則廢.在組織引導學生自學前，先向學生展示本節課的學習目標，讓學生在學習前就明確本節課的學習任務，這一點很有必要.而如何展示學習目標更有效，有待于我們在教學實踐中繼續探討.

1.袁亞良，江海人.一次市級說課比賽的成果展示與思考［J］.中學數學教學參考（中），2014（5）.WG

*本文為甘肅省教育科學“十二五”規劃2012年度立項課題《學案導學—自主合作教學模式在初中數學教學中的應用研究》的階段性成果，課題批準號：［2012］GSG200.