重建基于小組合作學習的數學高效課堂

吳子林

(連城縣實驗小學，福建 連城 366200)

重建基于小組合作學習的數學高效課堂

吳子林

(連城縣實驗小學，福建 連城 366200)

闡述小組合作學習的方法：巧妙分組，追求組員之間的合作；巧妙分工，促進組員之間的合作；巧妙組織，讓學生在合作中求知、發展。在“容易產生認知沖突的內容、開放性的內容和個人無法獨立完成的內容”時要安排小組合作學習；要真正留足小組合作學習的時間和組際交流的空間，讓學生在合作中學會學習，在學習中學會合作，在合作中發展。

重建；小組合作學習；高效

自課程改革以來，小組合作學習成為區分新課改課堂與傳統課堂教學的一個最明顯特征之一。它有力地改變了傳統課堂上教師“一言談”的專制，在課堂上給學生以自主、合作的機會，培養了學生的組內團體合作意識和組間良性競爭意識，發展了學生的人際交往與分辨的能力。高效的小組合作學習，能使小組成員之間相互促進，形成開放、互補、包容的學習氛圍；能提高學生的學習效率和學習興趣，增強學生的人際交往能力。小組合作學習雖然在當今課堂得以廣泛使用，但是在實際操作中卻一直存在著種種問題。如何重建基于小組合作學習的小學數學高效課堂，值得深思。

一、巧分組，追求組員之間的合作

1.合理搭配。就是把學習成績優劣、能力強弱、性別不同、性格和家庭背景有差異的學生分在一個小組內，注意男女生的人數要相對均衡，學優生、中等生、學困生的比例盡量做到1∶2∶1，使小組成員間保持一定的差異。由于每個小組都是異質的，所以就連帶產生了全班各小組間的同質性，達到“組間同質、組內異質”。[1]

2.動態分組。合作學習中的分組如果一直是固定結構，時間一長，就會使學生的參與興趣降低，因此可以通過動態分組進行調節。動態分組主要有自愿分組和按見解的不同隨機分成觀點不同的正、反兩組：自愿分組能調動學生的積極性，活躍課堂氣氛；分正、反組可以形成兩大陣營，讓學生更好地針對某一問題或觀點進行有效的辯論。

二、巧分工，促進組員之間的合作

合作學習特別強調每個人在小組合作中的責任，要使每個人都認識到，他們不僅要為自己負責，而且還要為小組的其他同伴負責。組員之間只有互相依賴，互相幫助，擰成一股繩，才能很好地完成合作學習的任務。

1.小組規模。學習小組的規模是不確定的。小組的人數，一般為4～6人。一開始，教師應有意識地安排2人小組，完成一些簡單的合作任務，讓學生慢慢學會合作。當學生已經初步學會小組合作學習，這時候小組的規模可適當加大。3人或4人合作學習，對空間場地的變化要求不是很高，較容易實現。

2.座位安排。小組合作學習時，要根據教學的內容和教學活動的組織形式將單一的“秧田式”座位進行適當變化。如討論、實驗等采用“風車型”“餐桌型”“口字型”，游戲、表演時采用“扇形”“馬蹄型”“U字型”，操作、競賽等采用“餐桌型”“品字型”“U字型”“梅花型”。[2]每個小組都要安排教師的座位，方便教師指導小組學習活動，拉近生生、師生之間的距離，建立起民主平等的師生關系，增加師生間、生生間交往的密度。

3.角色分配。小組組建后，不一定會出現教師預期的合作效應。小組內應分工明確，每一位學生都要在小組中擔任特定的角色：小組長，負責小組合作的組織和分工，保證每個人都有參與和表現的機會，組織有序地交流討論，防止“一哄而上”，最重要的是引導其他組員認真傾聽和補充，并根據組員在合作學習時參與度、學習態度等給組員評分；記錄員，負責記錄合作學習中小組的發現和小組討論的結果；材料管理員，負責領取和保管小組合作所需要的材料，確保合作有序進行；發言人代表小組在全班交流小組的研究成果。這樣，小組成員分工合作，共同實現小組目標。在學生已學會合作的基礎上，也可實行“角色輪換”，鼓勵每個成員在不同的角色中充分展現自己，使學生在合作中取長補短，促進知識、技能的迅速提高。另外，由于每個小組都有一個學習相對更困難的學生，所以還要給他安排一位學優生做他的“師傅”，“面對面”“一幫一”地幫助學困生。這樣，讓其他學困生也能跟上小組合作學習的步伐，達到共同進步的目的。

三、巧組織，讓學生在合作中求知、發展

《義務教育數學課程標準(2011年版)》指出：“數學活動是師生積極參與、交往互動、共同發展的過程。學生是數學學習的主體，教師是數學學習的組織者與引導者。”[3]在學生的合作學習時，教師雖然由臺前退到幕后，但是必須為學生搭建合作平臺，努力營造全員參與的生動活潑的合作氛圍。

1.合理安排合作學習的內容，讓學生在合作中求知

并不是所有的內容都需要學生合作學習的。選準、選精學習內容是確保合作學習實效性的重要因素。對于較簡單的學習內容，學生可以獨立自學或者由教師進行一般性教學；而相對復雜、需要探究的綜合性學習內容，則鼓勵學生采取合作學習的方式。

(1)容易產生認知沖突的內容。容易產生認知沖突的內容，讓學生口欲言而不能的問題，最值得合作學習。[4]針對學生在學習中產生的認知沖突，教師適時引導學生進行討論、辨析，讓學生在爭論中逐漸自悟，從而體現合作學習的價值。

(2)開放性的內容。一些具有開放性的問題，或者可用多種方法、多種策略解決的問題，是學生進行合作學習的很好資源。[5]筆者在教學“梯形面積的計算”時，學生能利用前面所學的平行四邊形和三角形面積公式推導的方法，用兩個完全一樣的梯形拼成一個平行四邊形推導出梯形面積公式。這時我問“還能不能用其他方法推導出梯形面積計算公式呢？”學生在獨立觀察、思考后，通過小組合作、動手操作，紛紛探索出不同的解決方法：有的將一個梯形分成兩個三角形(如圖1)，得出S=ah÷2+bh÷2=(a+b)h÷2；有的將梯形剪、拼成三角形如圖(2)，得出S=(a+b)h÷2；有的將梯形分成一個平行四邊形和一個三角形(如圖3)，得出S=ah+(b-a)h÷2=ah+bh÷2-ah÷2=ah÷2+bh÷2=(a+b)h÷2；有的將梯形沿兩腰的中點剪開，旋轉后拼成一個平行四邊形(如圖4)，得出S=(a+b)(h÷2)=(a+b)h÷2。這樣在合作交流中，既充分挖掘了每個學生的探究潛能，又培養了學生合作學習能力。

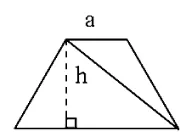
圖1

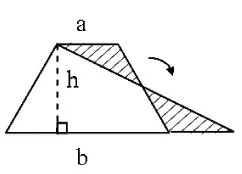
圖2

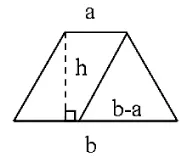
圖3

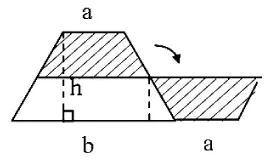
圖4

因為不同學生的知識基礎、能力、興趣、愛好等都是不盡相同的，每個學生思維的角度都可能不一樣，開放性的問題必然會引發學生多維度的思考，小組合作學習就能有效地實現互補。

(3)靠個人力量無法獨立完成的內容。當出現學生個人無法獨立完成、需要同伴的幫助才能完成的學習內容時，要組織小組合作學習。[6]如教學“統計”時，教師預設了“統計‘六一兒童節’班級聯歡會所需要購買的水果、茶點”的情境，由于人數多，每人所需要的品種數目、數量也多，學生自己獨自一個人統計一時忙不過來，這正達到教師所需要的效果——讓大家想到要尋求同伴的幫助，進行小組合作。然后組建學習小組，進行分工：有的統計蘋果的數量，有的統計香蕉的數量，有的統計瓜子的數量，有的統計花生的數量……一個一個記太慢，就畫“正”字來表示。好辦法在學生你一言我一語中就出現了。這樣，既讓學生親歷統計過程，體驗合作的威力，讓學生真正明白“為什么要合作”和“怎樣進行合作”。

2.真正留足合作學習的時空，讓學生在合作中發展

學生在教師的引導下獨立思考、自主探究的過程中總會發現問題，得出自己個性化的結論。對發現的問題總是希望得到同伴的幫助，對自己的發現更是想展示于眾，得到大家的驗證、肯定和贊揚。在教學過程中，教師要真正為學生留足合作學習的時空，以促進學生的發展。

(1)留足小組合作的時間。維果茨基提出了“最近發展區”，就是學生即將獲得并能夠獲得的經驗，但這種經驗現在暫時還不具備。學生通過自學后還不明白的問題，就是處在學生各自最近發展區的問題，教師應為學生留下足夠的合作交流的時間，讓學生談所得、提問題、議發現。

(2)留足組際交流的空間。學生在小組合作學習中，也常會出現“是什么”而說不清“為什么”的“憤悱”狀態，這時可允許學生跨組請教。如在教學“三角形的三邊關系”時，老師發兩根小棒給學生，要求學生用兩根小棒擺成三角形。有一個小組議論紛紛，問題在本小組得不到解決，學生就跨組向別組同學請教。通過組際交流，他們知道了用兩根小棒擺成三角形必須要再配上一根，才能圍成三角形。然后教師再引導學生思考：再配上一根多長的小棒，就能圍成一個三角形？有幾種配法？這樣，不僅使學生學會解決問題的辦法，獲得學習的經驗，還能讓學生體驗到合作學習的必要性，感受到合作學習給自己和他人帶來的快樂。

(3)留足學生爭辯的時空。學生在活動交往中，由于思維的不斷碰撞，問題不僅越來越多而且越來越尖銳。這時教師可從學生在課堂上生成的疑難問題中，抽取出與本節課有關的、有價值的問題，并提出來組織學生通過爭辯來解決。如教學五年級下冊數學拓展性知識“互質數”時，教師抽取一個學生質疑的問題：有什么辦法很快地判斷出兩個數是互質數？先鼓勵學生獨立思考，在學生有了自己的觀點、看法的基礎上，讓學生辯駁。學生甲說：“兩個數，其中一個是質數，那么這兩個數一定是互質數。”生乙馬上反駁說：“6和3這兩個數就不是互質數。”生丙又提出：“兩個數都是質數，這兩個數一定是互質數。”生丁馬上說：“3和3就不是互質數，應該說兩個不同的質數是互質數。”接下來學生又提了許多問題，如：兩個數都是合數，一個數是偶數另一個數是奇數，一個數是合數另一個數是質數，1和任何自然數等等，這樣的兩個數一定是互質數嗎？通過爭辯，學生終于弄清了成為互質數的兩個數的幾種情況，體驗到合作學習帶來的快樂。

“在合作中學會學習，在學習中學會合作”。有效的合作既是學習取得成功的條件，更是數學高效課堂的保證。重建基于小組合作學習的數學課堂，讓學生帶著自己的生活經驗走進課堂，同教材、教師、同學對話，在小組合作中自主探索，合作交流，親身體驗，生成自己獨特的、個性化的見解，獲得更多的數學活動經驗，獲得更多的學習樂趣，促進學習品質的全面提升，這是我們今后在數學教學中不斷探索研究的方向。

[1]劉吉林，王坦.合作學習的基本理念(一)[J].人民教育，2004(1).

[2]郭寶珍.數學教學中的“合作學習”[J].山西教育(教學)，2013(2).

[3]教育部.義務教育數學課程標準(2011年版)[S].北京:北京師范大學出版社,2012.

[4]王甲娜.哪些內容適合合作學習[J].基礎教育課程，2006(2).

[5]陳清容.為數學合作學習選準內容[J].人民教育，2004(3).

[6]樂華文.選準數學合作內容，確保合作學習實效[J].教育，2009(3).

2014-08-20

吳子林(1971- )，男，福建連城人，連城縣實驗小學高級教師。

< class="emphasis_bold">文章編號：1673-9884(2015)02-092-04

1673-9884(2015)02-092-04