用好、用足、用活小學數學教材中的情境

余秀麗

(古田縣教師進修校，福建 寧德 352200)

用好、用足、用活小學數學教材中的情境

余秀麗

(古田縣教師進修校，福建 寧德 352200)

教材的價值，最終是通過教師來實現的。面對教材中的情境，先“拿來”，而后認真、用心地去解讀。用好、用足、用活，讓其更好地服務于教與學，使教學更加豐富，學習更加有效。

教材；情境；用好；用足；用活

一個好的教學情境對教學能起到“四兩拔千斤”的作用，但要創設一個好的教學情境，對于廣大的忙碌在教學第一線的教師們，往往沒有超越教材另辟蹊徑去創設情境的時間、精力和能力。那么，如何“創造性地使用教材，積極開發、利用各種教學資源，為學生提供豐富多彩的學習素材”？[1]不妨用好、用足、用活小學數學教材上的情境。

一、用好情境

【案例】蘇教版義務教育教科書小學數學五年級上冊第59頁“除數是整數的除法”例4：下表是媽媽購買水果的數量和總價。算出每種水果的單價并填處下表。

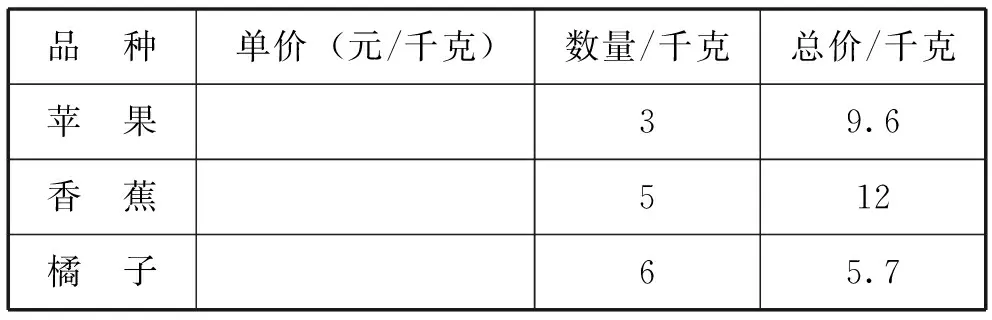
品 種單價(元/千克)數量/千克總價/千克蘋 果39.6香 蕉512橘 子65.7

1.師：周末，芳芳跟媽媽一起到超市買水果,遇到了一些與數學有關的問題,我們一起來看看。(出示課本主題情境圖)

師：怎樣求三種水果的單價是多少元，能列出式子嗎？(學生很快列出了三個除法算式，并由此自然地引入了新課)

2.每千克蘋果多少元？9.6÷3=？

師：9.6÷3=？能用已有的知識試著算一算嗎？

學生獨立嘗試后交流算法：

生1：9.6元=96角，96÷3=32(豎式略)，32角=3.2元。

生2：9.6元是9元6角，9元÷3=3元，6角÷3=2角，3元2角=3.2元。

生3：9.6是9個一和6個0.1，9個一÷3=3個一，6個0.1÷3=2個0.1，3個一和2個0.1合起來是3.2。

根據學生的回答，教師順學而導，逐步引導學生理解豎式計算中商的小數點的定位。

3.每千克香蕉多少元？12÷5=？

大部分學生列豎式得出：12÷5=2(元)……2(元)

師(指著這個商)：可以這樣表示嗎？

生(似有所悟)：好象從沒聽說過單價有“2元……2元”這樣子的。

師：單價的確不能這樣表示。那該怎么辦？余數2是表示什么？可以接著往下除嗎，為什么？

……

4.每千克桔子多少元？5.7÷6=？

師：5.7÷6=？個位不夠商1，怎么辦？

生：6千克桔子5.7元，說明每千克桔子還沒有1元錢，所以商是零點幾元，個位可以用0占位。

……

小數除法是四則計算的一個難點。教材別具匠心地創設了充滿生活味的情境——買水果，把三道例題串了起來。一方面，讓學生進一步感受計算是解決實際問題的需要；更主要的是借助情境激活已有知識、經驗，為理解本課意義、探索其中的算法起到調度經驗，啟迪思維的作用。

在上面的案例中，教師不僅利用情境創設了學生熟悉的購物情境，激發興趣，引入新課。而且，在三道例題的算法探索過程中，不斷地借助情境為理解算理、掌握算法提供支撐：例1中借助元、角之間的關系，理解商的小數點與被除數小數點對齊的道理；例2“這個商可以這樣(2……2)表示嗎？”面對計算中出現的新問題，再次利用情境中的生活經驗，理解“為什么要繼續除，為什么可以在余數后面添零繼續除”的道理；例3更是直接利用學生的生活經驗理解整數部分不夠商1用0占位的道理。

用好教材的情境，不僅把其當作引入新課的敲門磚，而且要發揮其解釋、溝通知識的價值，在學生已有的生活經驗、知識經驗和本課要探索的新知之間架設起橋梁，使教學過程自然順暢、樸實高效。

二、用足情境

蘇教版義務教育教科書三年級下冊第76頁例1：把一盤桃(4個)平均分給2只猴子，每只小猴分得這盤桃的幾分之幾？

1.教師先隱去題目，只出示猴子分桃的情境圖，并把桌上的桃子改成了一個，問：猴媽媽要把一個桃平均分給2只猴子吃，每只猴子吃這個桃子的幾分之幾？為什么？

2.把情境中的桃子改為一盤4個：現在猴媽媽拿出了一盤桃子平均分給2只猴子吃，每只猴子吃這盤桃子的幾分之幾？想一想該怎樣分，并拿出桃子圖分一分，再說一說。

學生操作后，教師配合課件，得出每只猴子分得這盤桃的1/2，初步體會把4個桃子看作一個整體，平均分成2份，這樣的一份也可以用1/2來表示。例題的教學原本至此可以圓滿畫上句號，但老師并不滿足于此，而是提出了新的問題：

3.如果這盤桃子有8個，這兩只猴子平均分，每只猴子分得這盤桃子的( )/( )？

4.如果這盤桃子有12個，這兩只猴子平均分，每只猴子分得這盤桃子的( )/( )？

5.在學生操作、討論得出正確答案后，教師引導學生進行觀察、比較、反思：

(1)思考：剛才這幾個問題的答案都是1/2，大家比較一下，第2～4題與第1題有什么不同？

生1：一盤桃子的數量不同。

師小結：對！第1題是我們已經學過的——把一個物體平均分成幾份，表示這樣的一份，就得到這個物體的幾分之一。2～4題是把4個、8個、12個桃子看作一個整體平均分，這是我們這節課要學習的新知識——一個整體的幾分之一。

(2)再思考：從第1題～第4題，一盤桃子的數量不同，為什么每只猴子分到的都是這盤桃子的1/2？

生2：因為都是把這盤桃子平均分成2份，每只猴子只分到其中的1份，所以都是1/2。

師：非常好！那如果猴媽媽買回一籃子桃子，還是平均分給這2只猴子，每只猴子分到這籃桃子的幾分之幾？

生3：不知道。一共幾個桃不知道，沒法分。

師：噢？不知道一共幾個桃就沒法分，真的嗎？(學生陷入思考，同桌小聲交流，有的學生在稿紙上畫。)

生4(遲疑地)：可能還是1/2。

師：還是1/2？有同意這種看法的嗎？為什么認為還是1/2？

生4：我也象上面一樣畫了一個圈表示一籃桃子，把它平均分2份，每份也是其中的1/2。

師演示課件，讓學生理解，每只猴子同樣也是分到這籃桃子的1/2。然后小結：不管多少個桃子，只要是平均分2份，其中的一份都是用1/2來表示。

(3)剛才我們認識了一個整體的1/2，你能畫圖表示出一個整體的1/2嗎？

……

在上面的教例中，教師充分利用教材情境，把學生帶進熟悉的“分桃子”的生活情境中，先是隱去例題的原題目，把桃子數量改為“一個”，借用這個情境很好地復習了“一個物體的幾分之一”，順利喚醒學生已有的知識經驗。然后，還是這個情境，解決了例題的問題后，教師沒有馬上鳴金收兵，而是連續利用情境，把桃子數量改為4個、8個、12個，讓學生分一分、填一填，豐富學生對1/2的感知。更可貴的是，在學生操作、討論得出一組“1/2”后，教師不失時機引導學生進行了三個層次反思：第一層求異比較——“大家比較一下，第2～4題與第1題有什么不同？”，通過與舊知的比較，讓新知更清晰，同時也把新知納入到原有的認知結構中。第二層是求同比較——“從第1題～第4題，一盤桃子的數量不同，為什么每只猴子分到的都是這些桃子的1/2？”通過這一問題的反思、交流，揭示新知共同的本質的屬性。尤其是“如果猴媽媽買回一籃子桃子，還是平均分給這2只猴子，每只猴子分到這籃桃子的幾分之幾？”的討論，拉長了學生從分桃子的生活情境向純粹的數學概念過渡的過程。第三層“能畫圖表示出一個整體的1/2嗎？”則給了學生一個內化的過程，也讓學生由分桃子這一具體情境激起的內在經驗明晰化。這一片斷的教學，教師在原情境的基礎上，把情境用足，巧妙的修改、添加、設問，充分挖掘了情境的智力因素，激發、引導學生積極思維，主動探究，拓展了思維空間，啟迪了學生的智慧。

“讓情境擁有“數學”的脊梁”，[2]用足情境，深入挖掘情境的利用價值，通過對情境的連續開發、多層設問，使得原本簡單的一道例題，變得厚實，使得數學本質得以充分突顯，也給了學生一片思維弛騁的天空。

三、用活情境

蘇教版義務教育教科書小學數學五年級上冊《小數大小比較》第39頁例7：

買一副三角尺用0.6元，買1本練習本用0.48元。三角尺和練習本，哪個貴一些？

教材是通過這個例子讓學生經歷小數大小比較方法的探索過程，發現、歸納小數大小比較的方法，但是，學生的學習過程中不可能只通過一、二個材料就能進行歸納、提煉，所以我們可把問題“三角尺和練習本，哪個貴一些？”稍做拓展，依次出示三個問題：

(1)小東有0.5元錢，夠買上面的哪樣文具？

(2)小麗有1元錢，夠買上面的哪樣文具？

(3)小明有0.45元錢，夠買上面的哪樣文具？

這樣變化后，一方面利用“錢夠不夠買東西”喚醒學生的生活經驗。另一方面，通過問題(1)中0.5元和0.6元的比較，巧妙地激活學生已有的相關舊知，為本課的自主探究做好知識、方法上的準備；而(2)(3)兩問，則提供了與原題不同的兩種類型的比較(整數與小數比較、整數部分和十分位都相同的小數大小比較)，從而為學生探索、理解小數大小比較方法和運用不完全歸納法進行小數大小比較方法的概括提供更為豐富的、可信的材料。

教材的情境雖是編者精心設計的，但其存在方式是靜態的、封閉的，又由于受篇幅的限制，很多時候，教材情境圖的容量和表現力顯得力不從心。這就要求，我們教師在運用教材情境之前，要先深入解讀情境，結合教學內容、學生的數學現實，對情境進行適當的修改、添加、拓展，把教材情境用活，使我們的教學更加豐富，學生的學習更加有效。

從某種角度講，教材的價值，最終是通過教師來實現的。所以，面對教材中的情境，先“拿來”，而后認真、用心地去解讀，用好、用足、用活，讓其更好地服務于教與學，是每位教師應該和能夠做到的。

[1]教育部.義務教育數學課程標準(2011年版)[S].北京:北京師范大學出版社,2012.

[2]丁國忠.讓情境擁有“數學”的脊梁[J].人民教育,2006(8).

2014-12-03

余秀麗(1970- )，女，福建寧德人，古田縣教師進修學校中學高級教師。

G427

A< class="emphasis_bold">文章編號：1673-9884(2015)02-0077-03

1673-9884(2015)02-0077-03