一道數(shù)學(xué)預(yù)賽試題的簡解及高考鏈接

☉山東省寧陽第一中學(xué) 陳新偉

一道數(shù)學(xué)預(yù)賽試題的簡解及高考鏈接

☉山東省寧陽第一中學(xué) 陳新偉

題目（2014年全國高中數(shù)學(xué)聯(lián)賽山東賽區(qū)預(yù)賽第13題）如圖1，設(shè)點O為橢圓的中心，過點A作長軸的垂線，垂足為M，連接AO并延長交橢圓于另一點B，連接BM并延長交橢圓于點C，問：是否存在橢圓，使得BA⊥CA？

點評：賽題是對橢圓一般性質(zhì)的探索，主要考查直線與直線、直線與橢圓的位置關(guān)系，題目涉及四點（點A、B、M、C，其中點A為“制高點”，其余點伴隨產(chǎn)生，點O為“關(guān)鍵點”，是橢圓的中心，也是弦AB的中點）、四直線、一曲線（橢圓），因題目針對一般性的探索，解答均為字母運算，一般方法運算量較大，學(xué)生不易順利解答.

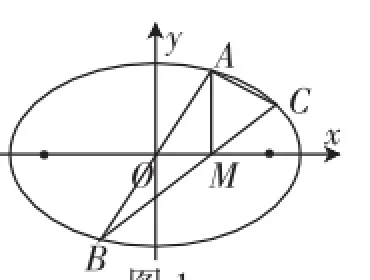
圖1

一、試題簡解

簡解：假設(shè)存在滿足條件的橢圓，使得BA⊥CA，不妨設(shè)橢圓的方程為y2），BC的中點為P（xP，yP），則

點評：簡解緊緊抓住“制高點A”和“關(guān)鍵點O”，利用“點差法”，設(shè)而不求，探索直線BC、AC、AB斜率之間的關(guān)系，尋求結(jié)論成立的充要條件，大大減少了計算量，并且得到了一些相關(guān)結(jié)論.

二、結(jié)論呈現(xiàn)

結(jié)論1在橢圓的內(nèi)接三角形中，若三角形一邊過橢圓的中心且不與坐標(biāo)軸重合，則另外兩邊的斜率之積為定值e2-1.

注：由簡解中的（*）式可得.

結(jié)論2設(shè)AB為過橢圓中心不與坐標(biāo)軸重合的任意一條弦，過點A作x軸的垂線，垂足為M，連接BM交橢圓于點C，則kAB·kAC=2（e2-1）.

結(jié)論3設(shè)AB為過橢圓中心不與坐標(biāo)軸重合的任意一條弦，過點A向橢圓的長軸作垂線，垂足為M，連接BM與橢圓交于點C，則BA⊥CA的充要條件是橢圓的離心率

注：賽題簡解過程可逆.

結(jié)論4設(shè)AB為過橢圓中心不與坐標(biāo)軸重合的任意一條弦，過點A作AB的垂線AC交橢圓于點C，連接BC交x軸于M，若直線AM不與y軸平行，則kBC=（1-2e2）kAM.

簡證：如圖2，設(shè)直線AB的斜率為k，A（x1，y1），由題意知B（-x1， -y1）由結(jié)論1，kBC·kAC= e2-1，故kBC=k（1-e2），所以直線BC的方程為y+y1=k（1-e2）（x+x1），則故所以kBC=（1-2e2）kAM.

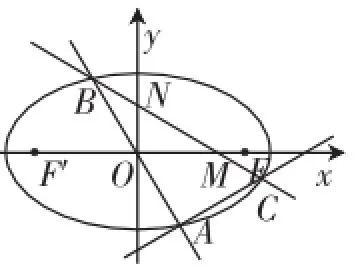
圖2

三、高考鏈接

例1（2011年全國高考江蘇卷理科第18題）如圖3，在平面直角坐標(biāo)系xOy中，M、N分別是橢圓的頂點，過坐標(biāo)原點的直線交橢圓于P、A兩點，其中點P在第一象限，過點P作x軸的垂線，垂足為點C，連接AC，并延長交橢圓于點B，設(shè)直線PA的斜率為k.

圖3

（Ⅰ）當(dāng)直線PA平分線段MN時，求k的值；

（Ⅱ）當(dāng)k=2時，求點P到直線AB的距離d；

（Ⅲ）對任意k＞0，求證：PA⊥PB.

例2（2014年全國高考山東卷文科第21題）在平面直角坐標(biāo)系xOy中，橢圓（a＞b＞0）的離心率為直線y=x被橢圓C截得的線段長為

（Ⅰ）求橢圓C的方程.

（Ⅱ）過原點的直線與橢圓C交于A、B兩點（A、B不是橢圓C的頂點），點D在橢圓C上，且AD⊥AB，直線BD與x軸、y軸分別交于M、N兩點.

①設(shè)直線BD，AM的斜率分別為k1，k2，證明存在常數(shù)λ使得k1=λk2，并求出λ的值；

②求△OMN面積的最大值.

（由結(jié)論4易得）.