高考圓錐曲線試題中揮之不去的切線“情結”

☉浙江省杭州師范大學附屬中學 蘇立標

高考圓錐曲線試題中揮之不去的切線“情結”

☉浙江省杭州師范大學附屬中學 蘇立標

近幾年的高考試題中對圓錐曲線的切線問題的考查已經不再是“羞答答的玫瑰靜悄俏地開”，而是逐步受到命題者的青睞，而且不斷地加大考查的力度，成為命題者情有獨鐘的切線“情結”，所以我們有必要對高考試題中圓錐曲線的切線問題進行梳理，以便理清高考復習的思路.

一、一道試題的探究

（1）求橢圓C的方程；

（2）設Q（x0，y0）（x0y0≠0）為橢圓C上一點，過點Q作x軸的垂線，垂足為E，取點連接AE，過點A作AE的垂線交x軸于點D，點G是點D關于y軸的對稱點，作直線QG，問：這樣作出的直線QG是否與橢圓C一定有唯一的公共點？并說明理由.

所以直線QG與橢圓只有一個公共點.

“記錄在紙上的思想就如同某人留在沙上的腳印，我們也許能看到他走過的路徑，但若想知道他在路上看見了什么東西，就必須用我們自己的眼睛.”德國哲學家叔本華的這番話從某種意義上也道出了探究學習的重要性，對于一些典型的高考試題，教師應積極地引導學生進行探究性學習，這樣有利于深化學生對數學知識和方法的理性認識，促進其創造性思維能力的發展，從而充分發揮學生的智能和潛能，所以我們對問題進行如下推廣探究：

推廣1：設Q（x0，y0）（x0y0≠0）為橢圓b＞0）上一點，過點Q作x軸的垂線，垂足為E，取點A（0，a），連接AE，過點A作AE的垂線交x軸于點D，點G是點D關于y軸的對稱點，作直線QG，則直線QG是橢圓C的切線（與橢圓C有唯一的公共點）.

推廣2：設Q（x0，y0）（x0y0≠0）為雙曲線（a＞0，b＞0）上一點，過點Q作x軸的垂線，垂足為E，取點A（0，a），連接AE，過點A作AE的垂線交x軸于點D，點G是點D關于y軸的對稱點，作直線QG，則直線QG是雙曲線C的切線（與雙曲線C有唯一的公共點）.

證明：由題意知，AD的方程為x0x-ay+a2=0，所以則QG的直線方程為x0y0x-

推廣3：設Q（x0，y0）（x0y0≠0）為橢圓C：b＞0）上一點，過點Q作x軸的垂線，垂足為E，取點A（0，a），連接AE，過點A作AE的垂線交x軸于點D，過點Q作橢圓C的切線QG交x軸于點G，則點G為點D關于y軸的對稱點.

證明：由題意知，AD的方程為x0x-ay+a2=0，所以則QG的直線方程為得到所以點G是點D關于y軸的對稱點.

推廣4：設Q（x0，y0）（x0y0≠0）為橢圓b＞0）上一點，過點Q作x軸的垂線，垂足為E，取點A（0，a），連接AE，過點Q作橢圓C的切線QG交x軸于點G，若點G是點D關于y軸的對稱點，則直線AD與AE垂直.

二、高考試題中切線問題

1.證明切線問題

例2（2012年安徽省高考）已知點F1（-c，0）、F2（c， 0）分別是橢圓（a＞b＞0）的左、右焦點，經過F1作x軸的垂線交橢圓C的上半部分于點P，過點F2作直線PF2的垂線交直線于點Q.證明：直線PQ與橢圓C只有一個交點（即直線PQ是橢圓C的切線）.

2.考查切線的幾何性質

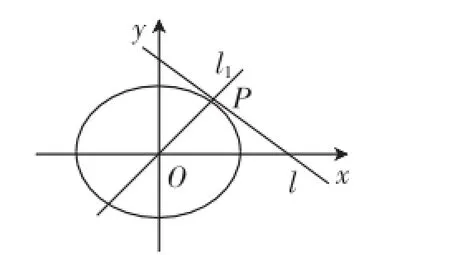
圖1

（1）已知直線l的斜率為k，用a、b、k表示點P的坐標；

（2）若過原點O的直線l1與l垂直，證明：點P到直線l1的距離的最大值為a-b.

（Ⅱ）設動直線l：y=kx+m與橢圓E有且只有一個公共點P，且與直線x=4相交于點Q.試探究：在坐標平面內是否存在定點M，使得以PQ為直徑的圓恒過點M？若存在，求出點M的坐標；若不存在，說明理由.

解析：（Ⅰ）因為|AB|+|AF2|+|BF2|=8，即|AF1|+|F1B|+ |AF2|+|BF2|=8，而|AF1|+|AF2|=|F1B|+|BF2|=2a，所以4a=8?a=1?b2=a2-c2=3，故所求橢圓方程為由于對任意m，k恒成立，所以聯立解得x1=1.故存在定點M（1，0），符合題意.

剖析：由題意易知動直線l是橢圓的一條切線，直線x=4為橢圓的右準線，定點M（1，0）恰好為橢圓的右焦點，這樣我們就可以把上述高考試題一般化，得到下面的推廣.

推廣：已知點F1（-c，0）、F2（c，0）分別是橢圓（a＞b＞0））的左、右焦點，過橢圓C的上半部分的一點P作橢圓C的切線PQ交橢圓的準線于點Q，則直線PF2與QF2相互垂直.

3.考查切點弦問題

例5（2013年廣東省高考）已知拋物線C的頂點為原點，其焦點F（0，c）（c＞0）到直線l：x-y-2=0的距離為設P為直線l上的點，過點P作拋物線C的兩條切線PA，PB，其中A，B為切點.

（Ⅰ）求拋物線C的方程；

（Ⅱ）當點P（x0，y0）為直線l上的定點時，求直線AB的方程；

解析：（Ⅰ）依題意，設拋物線C的方程為x2=4cy，由結合c＞0，解得c=1，所以拋物線C的方程為x2=4y.

（Ⅱ）拋物線C的方程為x2=4y，即求導得y′=

同理可得切線PB的方程為x2x-2y-2y2=0.

因為切線PA，PB均過點P（x0，y0），所以x1x0-2y0-2y1= 0，x2x0-2y0-2y2=0.

所以（x1，y1），（x2，y2）為方程x0x-2y0-2y=0的兩組解.

所以直線AB的方程為x0x-2y-2y0=0.

1.蘇立標.同根同源的兩道圓錐曲線高考試題的剖析［J］.中學數學（上），2012（10）.