培育學生解題的六種意識突破向量問題的解題瓶頸

☉江蘇省常熟市滸浦高級中學 殷偉康

·江蘇省常熟市殷偉康名師工作室·

培育學生解題的六種意識突破向量問題的解題瓶頸

☉江蘇省常熟市滸浦高級中學 殷偉康

平面向量是高中數學的重要內容之一，是溝通代數、幾何、三角等內容的橋梁，它具有極其豐富的實際意義和背景及廣泛的應用.平面向量具有“數”與“形”雙重身份，兼具代數的嚴謹與幾何的直觀，銜接著數學中“地位不凡”的兩大板塊.鑒于平面向量內容的上述特點，其深受命題者的青睞.近幾年江蘇省高考時常呈現“富有創意、獨具魅力、難度適中”的試題，成為高考試卷中的一大亮點.然而，許多學生即使到了高三對向量的學習還尚未真正入門，沒有形成有效的“向量解題意識”，遇到較靈活的向量問題就不知所措，思維就沒有了方向，導致解題時頻頻出錯.嚴世健教授認為：數學意識，是指人們在數學學習、數學應用的過程中，逐漸形成的對數學的見解和看法.它包括感性階段和理性階段，它具有識別、指向和選擇的功能.筆者根據自己二十多年的教學實踐經驗，探索出了從培育學生的“六種意識”入手，幫助學生形成“向量解題意識”，突破向量問題的解題“瓶頸”，取得了良好的教學效果.

一、基底意識：將未知化為已知，促使復雜問題有序化

例1（2014年高考江蘇第12題）如圖1，在平行四邊形ABCD中，已知AB=8，AD=的值是________.

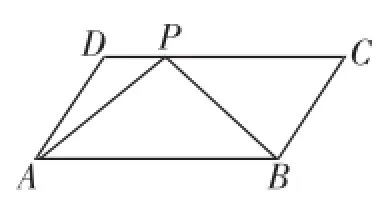
圖1

教師：為什么選取→作為一組基底呢？

教師：如何求解呢？

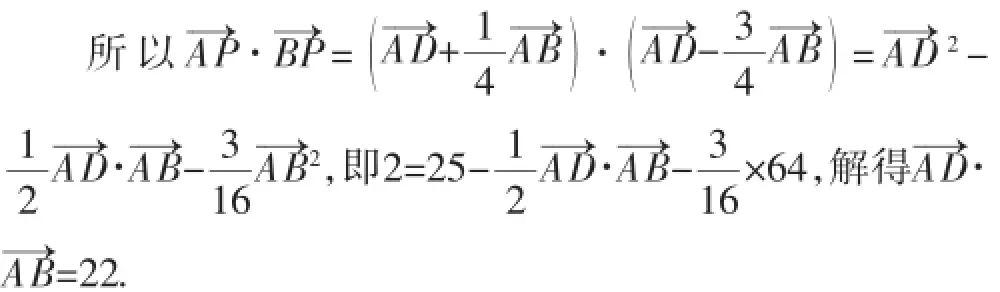
教師：解決本題的關鍵是什么？

學生3：科學合理地選擇基底，用基底來表示圖形中相關的向量（即用向量的線性關系描述幾何元素間的關系）.

教師：這種求解方法就是“基底化”方法，即“基底”意識.所謂“基底”意識，是指有預見性地、合理地選取基底，并用基底來表示圖形中的其他相關的向量，以實現轉化與化歸的一種思維方式.“基底”意識的本質就是平面向量基本定理的靈活運用，難點是如何選取恰當的“基底”以有利于簡化運算.

二、平方意識：把握向量的代數特征，實現向量運算數量化

例2（2013年蘇南四市第二次調研測試第12題）已知向量a、b滿足|b|=1，且對一切實數x，a+xb恒成立，則a與b的夾角大小為_________.

學生4：設a與b的夾角為θ，由|a+xb|2≥|a+b|2及|a|=cosθ-1≥0對一切實數x成立，整理得（x-1）cosθ≥1-x2，化簡得對一切實數x成立，此時y=-1-x的最小值不存在，下面不知如何求解？

教師：哪位同學來分析一下學生4的解法？

學生5：學生4的錯因是在進行變量分離時，沒有對字母x進行分類討論.

教師：為什么要對字母x進行分類討論呢？應該如何合理討論呢？

學生5：因為不能確定x-1與0的大小關系，其影響不等式符號的變化，所以要對字母x進行分類討論.

教師：學生5的分析相當到位，運用變量分離法處理不等式恒成立問題時，首先應該對有關變量進行分類討論.有無其他方法？

學生6：設a與b的夾角為θ，由|a+xb|2≥|a+b|2，得x2+對一切實數x成立，則Δ=

教師：有無其他解法？

圖2

教師：學生6運用“平方法”解題策略，把x2+cosθ-1≥0看作關于x的一元二次不等式對一切實數x恒成立，運用判別式Δ≤0求解即可；學生7運用數形結合思想，借助平面幾何知識進行求解，直觀快捷.上述解法中蘊含著怎樣的解題意識？

學生8：“圖形”意識，還有“平方”意識.

教師：很好！其中所謂“平方”意識，是指合理地運用向量中的重要等式a2=|a|2，將向量的模、向量的夾角和向量的數量積有機地聯系起來，即將向量問題迅速代數化，從而使向量問題迅速獲解的一種思維方式.因而在解向量題時要形成“遇模則平方”的意識.

三、建系意識：依據幾何特征合理建系，促使向量問題坐標化

例3（2014年南京市第二次高考模擬試卷第12題）在Rt△ABC中，CA=CB=2，M、N是斜邊AB上的兩個動點，則的取值范圍為__________.

學生9：可以通過建立直角坐標系進行求解.

教師：如何合理構建坐標系？怎樣用坐標來表示點M、N？

學生9：根據所給三角形為直角三角形，以CA、CB所在直線分別為x、y軸，建立如圖3所示的平面直角坐標系，設M（x，y）（0≤x≤1），則x+ y=2?y=2-x，即M（x，2-x）.

教師：那么點N呢？

學生9：設N（x0，y0），由點N在線段AB：x+y=2上，且可以列出方程組，通過解此方程組，用M的坐標（x，y）來表示點N的坐標.

圖3

教師：上述解題方法稱之為“坐標法”.所謂“建系”意識，是指通過建立直角坐標系，將向量改用坐標來表示，使研究對象有簡潔的代數表達式，將向量問題轉化為代數問題來處理的一種思維方式.“坐標法”是解決向量問題的一條重要途徑，依據所給條件中的正方形、矩形、直角三角形、等邊三角形或直角梯形等圖形，容易想到建立直角坐標系.其優點是思維方式比較“固定”，容易掌握，關鍵是合理地建立直角坐標系，準確算出關鍵點的坐標.所以當用別的方法難以奏效時，不妨用“坐標法”來嘗試一下.

四、圖形意識：靈活建構平面圖形，凸顯向量問題直觀化

例4（2011年蘇南四市第二次調研測試第12題）平面內兩個非零向量α、β滿足|β|=1，且α與β-α的夾角為135°，則|α|的取值范圍是________.

學生11：老師，我是這樣想的，由β-α聯想到平面向量的減法法則，構造三角形，進行求解.設與β-α的夾角為135°，得∠OAB=45°（如圖4）.在△AOB中，僅知其一個內角∠OAB及對邊OB，不知如何確定OA的取值范圍.

教師：對于三角形中邊與角的問題，我們常用什么方法來處理？

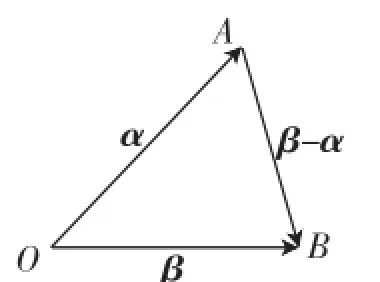
圖4

學生12：正弦定理與余弦定理.

教師：這時用哪個定理比較適宜？

教師：現在解題的關鍵是什么？

學生12：確定∠OBA的取值范圍.由∠OAB=45°可知0°＜∠OBA＜135°，則0＜sin∠OBA≤1，所以0＜OA即

教師：很好！通過構造三角形，將平面向量問題轉化為平面幾何模型問題，憑借解三角形知識獲得輕松的解法.能否受此啟發，作進一步的探究呢？

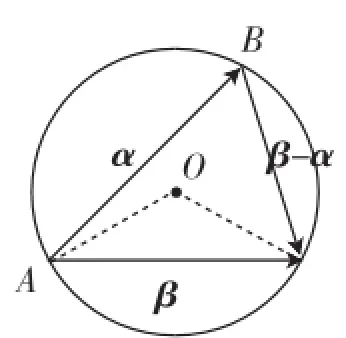
圖5

教師：其實學生13是抓住定線段的張角是定值的動點軌跡，它是以該線段為弦的一段圓弧，根據問題所給信息，通過數形聯想，挖掘其平面幾何背景，進行圖形表征，利用轉化思想，巧妙地解決了平面向量問題.這種解法中蘊含著怎樣的解題意識？

學生14：“圖形”意識.

教師：所謂“圖形”意識，是指能主動挖掘向量問題的幾何背景，構造圖形（三角形、平行四邊形、圓等），用“形”解題的一種思維方式.這種解題方法稱之為“幾何法”，即圖形化策略，體現了數形結合思想.運用圖形意識，將向量問題置于適當的幾何背景之中，各種數量關系在圖形中簡單明了，就能夠使抽象的向量問題直觀化，實現快速解題之目的.

五、引參意識：引進適當的參數，促使向量問題簡單化

例5已知直角梯形ABCD中，AD∥BC，∠ADC= 90°，AD=2，BC=1，P是線段DC上的動點，則P→→A+3P→→B的最小值為______.

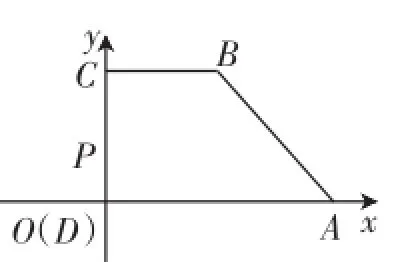
圖6

學生15：由“建系”解題意識可知建立如圖6所示的坐標系，則A（2，0）.設P（0，y），則P→→A=（2，-y），但是不知怎樣用坐標來表示

教師：誰來幫學生15解決這一困惑？

教師：有無異議？

學生17：不嚴謹，其中P（0，y）中的y要滿足0≤y≤h，取得最小值5.

教師：補充得很好！上述解法中蘊含著怎樣的解題意識？

學生18：“建系”意識和“引參”意識.

教師：所謂“引參”意識，是指在研究向量問題時，引入適當的參數，為向量問題的順利解決鋪路搭橋的一種思維方式.適當地建立坐標系和引入參數，使所要研究的向量有簡潔的代數表達式.

六、“點積”意識：適當進行數量積運算，促使向量問題代數化

例6（2009年高考安徽卷理科第14題）給定兩個長度為1的平面向量它們的夾角為120°，如圖7，點C在以O為圓心的圓弧AB上變動，若其中x、y∈ R，則x+y的最大值是________.

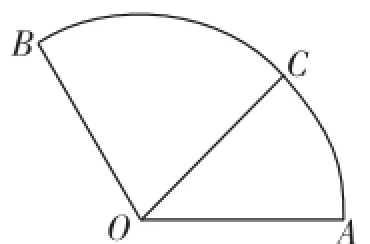
圖7

學生19：將向量式O→→C=xO→→A+yO→→B數量化，目標是要建立x+y的對應函數式.

教師：如何實現目標呢？

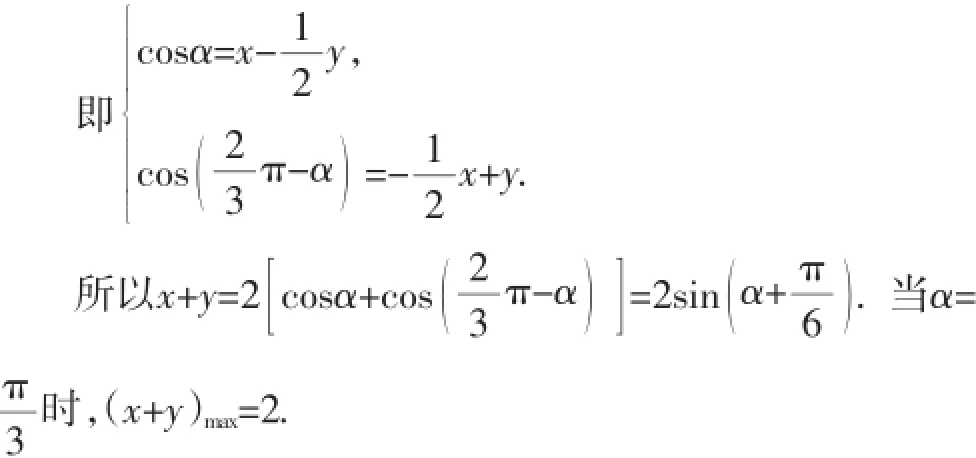
教師：這種處理方法，就是“點積”法.所謂“點積”意識，就是在一個含有向量關系的等式兩邊同時“點積”一個適當的非零向量，把有關向量關系的等式轉化為代數方程，實現化簡之目的的一種思維方式.

教師：有無其他解法？

總之，在平面向量復習課中，教師要強化培育學生的“六種向量解題意識”，達到“授之以漁”的目的，并引導學生總結提煉其中蘊含的數學思想方法，讓學生進一步理解和把握變量分離法、數形結合方法（基于幾何表示的幾何法，基于坐標表示的代數法）、方程思想、化歸與轉化思想方法的實質，積累解題經驗，形成“向量思想”，發展思維能力.

1.盧明.平面向量復習要強化“5種意識”的培養［J］.中學教研（數學），2014（4）.

2.殷偉康.聊題——數學學習因你而富有活力［J］.數學教學研究，2013（7）.

3.殷偉康.糾錯——高三數學復習不可或缺的重要環節［J］.中學數學（上），2014（3）.

4.曹軍.高中向量教學的誤區及思考［J］.中學數學教學參考（上），2014（1-2）.