解題教學中“數形結合思想”培養的嘗試與思考
——高三函數專題復習實踐研究

☉上海市桃浦中學 張正麗

解題教學中“數形結合思想”培養的嘗試與思考
——高三函數專題復習實踐研究

☉上海市桃浦中學 張正麗

把數量關系的研究轉化為圖形性質的研究，或者把圖形性質的研究轉化為數量關系的研究，這種解決問題過程中“數”與“形”相互轉化的研究策略，就是數形結合思想.數形結合思想就是要使抽象的數學語言與直觀的圖形結合起來，使抽象思維與形象思維結合起來.在使用過程中，由“形”到“數”的轉化，往往比較明顯，而由“數”到“形”的轉化卻往往給學生的解題帶來很大的困擾.因此，數形結合思想的培養更需偏重于由“數”到“形”轉化的訓練.

數形結合是一種很重要的數學思想.近年來全國各地的高考題中考查數形結合思想與各章節知識點結合的題型不在少數，尤其是填空選擇題中出現較多.在研究函數的圖像與性質時常常要用到數形結合的思想，若能正確分析題設并畫出函數的圖像，往往能事半功倍.筆者在高三函數專題復習中進行了實踐探索，結合近年來的高考題及模擬題，帶領學生對數形結合方法在研究函數性質方面的應用作一些分析與小結.

一、利用數形結合，合理分類討論，完善解題思維

在解決函數問題時常常需要利用函數的圖像輔助解題，利用數形結合，可以讓學生注意到問題解決需要分類討論，容易讓學生在解題過程中形成縝密的思維習慣，提高解題效率.

教學片段一：

例1設函數f（x）=x|x-a|，若對任意x1，x2∈［3，+∞），x1≠x2，不等式恒成立，則實數a的取值范圍是_____.

大約兩分鐘后，開始提問.

師：剛才兩位同學說得都不錯，那么請大家再考慮一下，對對稱軸的分類討論是否全面了呢？

生4：還缺一個等于零的情況，如圖3所示.

圖1

圖2

圖3

師：回答得非常好.下面就請大家結合這三位同學的想法完成這道題……

反思1：大部分學生看到含有絕對值的函數解析式時，首先會想到改寫成分段函數的形式，而且也知道此類問題往往需要進行分類討論，但是常因考慮問題不夠全面，思路不完整，容易出現漏解的情況.因此，需要引導學生體會在解決該類問題時使用數形結合方法對合理實施分類討論有很大幫助.

二、利用數形結合，化繁為簡，優化解題策略

教學片段二：

例2已知函數f（x）=|log2x|，正實數m，n滿足m＜n，且f（m）=f（n），若f（x）在區間［m2，n］上的最大值為2，則m、n的值分別為（）.

在巡視學生的解題過程，發現了以下一些解法：

（1）看到f（x）=|log2x|中有絕對值，第一反應是去絕對值，寫成分段函數形式.

（2）考慮到“f（x）在區間［m2，n］上的最大值為2”，學生就開始分類討論，即“f（m2）=2或者f（n）=2”，再結合“f（m）=f（n）”和“m＜n”的條件求出n和m.此過程計算量還比較大，且有學生未考慮m，n的大小關系，所以出現多解的情況.

通過巡視發現一部分學生雖有大致的解題思路，但沒有意識到如果能適當借助函數的圖像數形結合來解題，就可以避免分類討論.因此，筆者根據學生解題中出現的障礙，通過下列問題引導學生重新思考本題的解題思路與步驟.

（1）畫出函數的圖像，并觀察函數f（x）=|log2x|有何特征.

（2）如何利用條件“0＜m＜n時，f（m）=f（n）”確定m，n的位置.

（3）嘗試在圖像（如圖4）中標注出［m2，n］的大致位置，觀察能否確定在何處取到最大值.

反思2：在解題過程中，常常會遇到考查函數圖像與性質的一類題型，經常要用到數形結合的思想，有時還要用到分類討論，若能恰當使用數形結合思想，有時也可以避免分類討論，化繁為簡.因此，在運用數形結合思想解題過程中要充分考查數學問題的條件與結論之間的內在聯系，既分析其代數意義，又揭示其幾何意義，將數量關系和空間形式巧妙結合，來尋找解題思路，使問題得以解決.

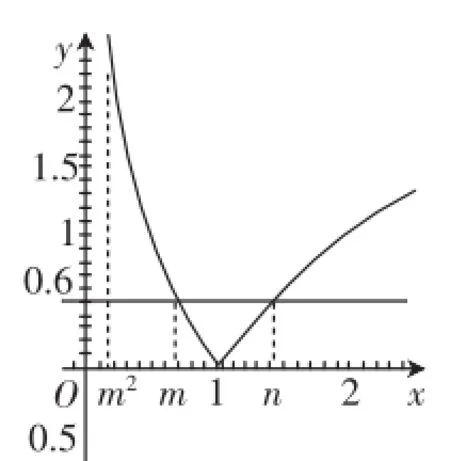
圖4

三、利用數形結合，構造函數解決方程問題

在函數與方程的專題復習后，給學生留下了一道思考題：“若關于x的方程有四個不同的實數根，則實數k的取值范圍是______.”第二天批改作業的時候，發現學生的作業中有幾種解題方法非常的漂亮，決定在課堂上展示，以此鼓勵其他學生也積極地思考問題.

教學片段三：

課堂上，先極力稱贊了給出完全正確解題過程的兩位學生，并且請他們分別講解了自己的思維過程.

生1：（圖5）首先考慮x=0是方程的一個根，然后方程兩邊是可以約掉|x|的，那么方程就應該是有三個不同的非零的根，即等價于考慮與y=k（x-3）的圖像有三個交點.因為函數y=k（x-3）的圖像是過定點（3，0）的，而是偶函數，由于x＜0時必有一個交點，故只需要考慮x＞0時，方程有兩個不同的實數根，所以k

生2：（圖6）同樣我也是看出x=0是方程的一個根，然后當x≠0時，就討論應有三個不同的交點，畫出的圖像后發現在k＜0時，必有一個負根，故只需考慮方程=kx在（0，3）內有兩個不同的實根即可，后面做的過程和剛才的同學是一樣的了.

圖5

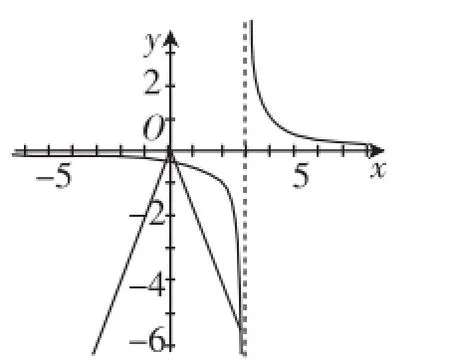
圖6

聽完這兩位同學的發言后，其他學生都非常的驚訝，這時課堂的氣氛異常活躍起來了，都七嘴八舌開始討論起來，有的說我怎么沒有想到呢，有的是沒發現x=0是方程的一個根，還有的說自己也是按照這樣的思路做的，但是做了一半卻做不下去了……

（學生們都在討論著）這時有一個學生舉手了.

生3：剛才他們的方法都是發現了x=0是一個根，先化簡了，但是我做的時候沒有想到，就想直接轉化為找函數有四個交點，可我沒有做出來，是不是這樣做不了呢？

師：這位同學的問題提得非常好.在你們的作業中，老師發現有幾位同學也是用這種方法做的，但是解題過程中存在一些問題，都沒有解下去.其實這種方法完全是可以解題的.

然后筆者提示并引導學生畫出了這兩個函數的圖像（圖7），讓學生完成此方法的解題.

（大約過了五分鐘）又有學生舉手了.

生5：老師，從這張圖中發現x=0肯定是一個根，既然這樣，那不如找函數它們的圖像應該有三個交點，豈不是更簡單嘛？

師：恩，觀察很仔細啊！那么函數y=|x|（x-3）的圖像怎么畫呢？

生5：（主動到黑板上畫出函數的圖像，如圖8）可以先將y=|x|（x-3）寫成分段函數然后函數是常值函數，圖像是一條平行于x軸的直線，這樣從圖中直接就看出范圍了.

圖7

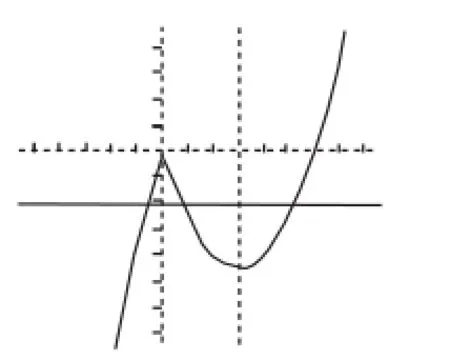
圖8

聽完這位學生的解釋，其他學生也更驚訝了：對啊，這個方法更簡單呀，一下子就求出范圍了……

師：這位同學的想法太好了.完全是正確的，而且你的方法也是非常簡單的，請大家按照這個思路來完成解題……

看到課堂的氣氛如此活躍，學生討論得這么的津津有味，并且很好地掌握了絕對值函數，筆者感到非常的欣慰.

反思3：本題考查的是學生能否正確運用函數方程的思想將求方程解的問題等價轉化為函數圖像交點的問題.學生在此類問題的解題過程中往往不能等價轉化，就會出現漏解、錯解.上述四種方法也正是數形結合思想在解函數方程問題過程中的充分體現.恰當地使用數形結合可以將抽象問題具體化，甚至有時能很快從圖像中找出答案.在此也應須遵循兩個基本原則：（1）盡量使其中一個函數不含參數，這樣可以固定一個函數圖像；（2）所找的兩個函數盡量是比較常見的、已學過的、形式相對簡單一點的.

在完成本題講評之后，為了及時鞏固學生對此類問題的掌握程度，筆者當場又給學生出了一道題，如下：

此題要求學生獨立完成，大約六分鐘后查看完成情況，發現學生的回答過程基本都正確.

反思4：“數”與“形”作為數學研究的兩個基本對象，既是統一又是對立.運用數形結合思想解題時，有時把數轉化為形，以形直觀地表達數來解決，往往使復雜問題簡單化、抽象問題具體化.但是若構圖不準確、不完整，數與形之間就會不等價，易造成錯解或漏解.因此，在數形轉化結合的過程中必須遵循下述原則：轉化等價原則；數形互補原則；求解簡單原則.當然在解題教學滲透數形結合的思想時，應指導學生掌握以下兩點：（1）善于觀察圖形，以揭示圖形中蘊含的數量關系；（2）正確繪制圖形，以反映圖形中相應的數量關系.切實把握“數”與“形”的對應關系，以圖識性，以性識圖.

四、對在解題教學中有效提高學生數形結合能力的一點思考

“數形結合”作為數學中的一種重要思想，在高中數學中占有極其重要的地位.關于這一點，查查近年高考試卷，就可見一斑.在多年來的高考題中，數形結合應用廣泛，大多是“以形助數”，比較常見的是在解方程、解不等式、求函數的最值、求復數和三角函數等問題中，巧妙地運用“數形結合”思想解題，可以化抽象為具體，事半功倍.

我們在教學過程中必須注意培養學生的數形結合思想.教師要引導學生根據問題的具體情況，注意改變觀察和理解問題的角度，揭示問題的本質，用“數”的準確澄清“形”的模糊，用“形”的直觀啟迪“數”的計算，從而使問題得到解決.在平日的教學中，教師要緊緊抓住數形轉化的策略，溝通知識聯系，激發學生的學習興趣，提高學生的思維能力.而且數形結合也不能只作為解題工具，只有充分揭示出數形結合的意義，深入挖掘其教育價值，數形結合在后續學習中才會有更旺盛的生命力，高中數學教學中數形結合提高解題能力的研究也才會有更寬、更好的奠基.

1.薛黨鵬.函數的圖像與性質［J］.中學數學教學參考（上），2012（1-2）.

2.［美］G.波利亞.怎樣解題［M］.上海：上海科技教育出版社，2005.

3.趙久勇，王梅蓉.數形結合應用中的錯誤剖析［J］.高中數學教與學，2011（11）.