改進的隨機共振和EMD混合模型用于轉子早期故障檢測

張海如， 王國富， 張法全， 葉金才

(1.西安電子科技大學電子工程學院，陜西西安 710071;2.桂林電子科技大學信息與通信學院，廣西桂林 541004)

0 引言

旋轉機械作為重要機械結構，已經在石化、電力、冶金和航空航天等國民經濟和國防事業的多個領域得到了廣泛應用，并且正朝著高速化發展。但由于機械部件潤滑不良、防塵防潮不嚴密、摩擦不均勻、使用壽命等多種因素，容易導致運行的設備發生各種機械故障，而且故障初期征兆難以察覺，經常是出現機器高溫、跳動幅度大、異響等破壞性警示時，才發現故障，這往往會帶來巨大的生命和財產損失。因此，轉子早期故障檢測得到了國內外相關領域專家和學者的廣泛關注和研究［1－7］。高速旋轉機械轉子早期故障信號非常微弱，且具有復雜的非線性和非平穩隨機性，這造成基于線性平穩理論發展而來的傳統微弱周期信號檢測技術難以適用。為了實現轉子早期故障檢測，能處理非線性和非平穩信號且具有良好時頻分析特性的小波變換和經驗模態分解(empirical code decomposition，EMD)得到了一定的研究，并且取得了一定的成果，人們分別提出了改進的諧波小波方法［8］、粒子群優化最小二乘小波支持向量機方法［9］、雙樹復小波域隱Markov樹模型降噪方法［10］，這些改進的小波變換方法在旋轉機械轉子早期故障檢測中起到了一定的作用，但是小波變換只有選擇了合適的小波基函數才能發揮作用，而且一旦選擇了基函數，在整個檢測過程中都不能改變，這會存在較大的漏警概率;還有人提出EMD分解與敏感度評估算法相結合的方法［11］和EMD分解與廣義維數相結合的方法［12］用于旋轉機械故障檢測，這些改進EMD分解具有一定的應用價值，但是在EMD分解時仍存在端點效應，且在強噪聲背景下進行EMD分解時，分解得到的各個基本模式分量(intrinsic mode functions，IMF)存在嚴重的頻率混跌失真，這會對轉子早期故障檢測造成巨大影響，為了使漏警率為零，這些方法會帶來較大的虛警率。此外，由于隨機共振系統具有能在極限信噪比下檢測微弱周期信號的功能，人們提出了多種改進的隨機共振系統用于早期機械故障檢測［13－15］，但是由于工業現場各種隨機噪聲的存在，可能導致隨機共振系統發生虛警，將噪聲干擾誤檢測為故障信號。

針對現有旋轉機械轉子早期故障檢測方法的不足，本文建立了尺度變換隨機共振降噪下的EMD分解模型，該模型充分利用了尺度變換隨機共振在全頻段內自適應檢測微弱周期信號所含頻率的能力和EMD分解對多頻混跌信號自適應分解的能力，并通過對EMD分解出的各個IMF進行處理，以還原出共振頻率對應信號的幅度值，以其幅值大小判斷隨機共振系統是否發生虛警，從而保證該模型對轉子早期故障檢測的準確性。

1 混合模型用于轉子早期故障檢測

1.1 尺度變換隨機共振系統

隨機共振系統能在極低的信噪比下提取微弱周期信號，但只適用于小參數信號，為了克服這一不足，已提出了尺度變換隨機共振降噪的方法［15］，該方法能在全頻段范圍內自適應地檢測到待測信號所含頻率分量，其實現步驟。

1)將含噪信號sn(t)輸入以非線性朗之萬方程構造的隨機共振系統。

隨機共振系統方程為

式中:s(t)為待測信號;n(t)為待測信號所含噪聲成分;x為輸出信號;a、b為系統的非線性參數，其值根據實際情況可進行調整。

2)步驟1)中若檢測到共振頻率fi，則將該信息保存并從原含噪信號sn(t)中濾除該分量，得到新的含噪信號sn(t)，重新執行步驟1);否則，執行步驟3)。

3)對當前含噪信號sn(t)進行尺度變換，將其頻率值縮小10倍后，重新執行步驟1)，重復該過程，直到頻率值的總的縮小倍數是待測目標信號預計最大頻率值的100倍時，執行步驟4)。

4)將檢測到所有頻率分量fi進行反尺度變換，還原出實際頻率值。

1.2 EMD分解原理

EMD分解的基本原理是將原始輸入信號分解成一系列IMF的組合，然后針對具體的應用環境進行后續的分析處理，以提取待測信號的本征信息。能進行EMD分解的信號必須具備兩個條件，分別是:待測信號的數據序列極值點和過零點的個數最多相差一個;局部極大值和極小值擬合的上下包絡線要局部關于坐標軸對稱。通過EMD分解能將待測信號的數據序列x(t)分解成式(2)，分解的詳細步驟可參考文獻［16］。

式中:ci為n個IMF;rn為殘余分量。該分解過程只依賴于原始信號序列的固有特征，是靠經驗知識自適應完成的，而且分解提取到的各個IMF具有平穩性，可用于對原始信號序列進行后續處理。EMD分解的過程可以看成是一個帶通濾波的過程，每個ci代表一個頻段的信號分量，但是由于實測信號受到各種噪聲干擾，各個IMF會發生頻率混跌失真，給后續信號處理帶來麻煩。因此，對信號進行分解前進行降噪處理是很必要的。

1.3 轉子早期故障檢測算法

尺度變換隨機共振降噪下的EMD分解用于旋轉機械轉子早期故障檢測，其實現步驟如下，圖1為其實現流程。

圖1 混合模型的流程Fig.1 Flow diagram of the conjoint model

1)將轉子的原始含噪信號x(t)通入尺度變換隨機共振系統，提取出x(t)所含的各個頻率分量，并將這些頻率分量保存在數據集合W={fi|i=1，2，…，n}中。重復執行該過程，直到W為非空集合時，執行步驟2)。

2)根據數據集合中所含的各個頻率分量，W采用帶通濾波器對原始信號x(t)進行分段濾波處理，得到新的僅保留目標頻率分量的信號x'(t)。

3)對x'(t)進行EMD分解，得到其所含的各個IMF，并通過對各個IMF進行功率譜估計找到目標頻率值對應的IMF。由于x'(t)是降噪后的信號，此時的各個IMF頻率單一，不存在頻率混跌失真。

4)對各個有用的IMF進行處理，得到其對應的幅度特征。

求取各個IMF的幅度特征的步驟為:a)為了去除EMD分解的邊界效應的影響，對ci兩端各去除其對應頻率的兩個周期的信號值，用其中間區域c'i求取該頻率信號對應的幅度值;b)對c'i取絕對值得到c″i，求取c″i的各個局部極大值，并將其存入數據集合Mi={Aj|j=1，2，…，n}中;3)求取Mi平均值Ai，Ai作為ci的幅度值。

5)根據ci的幅度值Ai的大小驗證尺度變換隨機共振系統是否發生虛警，以使整套系統達到零虛警率。

在具體的應用中，首先采集多組已知發生故障的旋轉機械的振動信號，并統計出其最小值θmin，為了減小虛警事故的發生，早期故障的閾值設為θmin/2。

2 仿真實驗研究

已知強噪聲背景下的含噪信號sn(t)=s(t)+n(t)，式中n(t)為強度D=0.5的高斯白噪聲，目標信號s(t)=A1sin(?1t)+A2sin(?2t)，其中，A1=A2=0.005 A，?1=10 Hz，?2=30 Hz。將sn(t)通入如圖1所示的尺度變換隨機共振降噪下的EMD分解系統，以驗證該系統的性能，原始的含噪信號sn(t)如圖2所示。

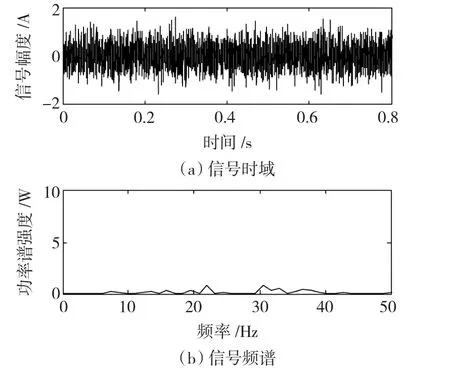
圖2 原始含噪信號Fig.2 The original signal with noise

1)將sn(t)通入尺度變換隨機共振系統，只有當將sn(t)的頻域壓縮1 000倍時，系統才會發生共振，共振頻率分別為0.01 Hz和0.03 Hz，所以判定原始含噪信號只含有10 Hz和30 Hz的頻率分量。共振時輸入隨機共振系統的信號如圖3所示，系統輸出信號如圖4所示。

圖3 共振時隨機共振系統的輸入信號Fig.3 Input power spectrum of the bistable system at resonance frequency

圖4 共振時隨機共振系統的輸出信號Fig.4 Output power spectrum of the bistable system at resonance frequency

2)采用帶通濾波器對原始含噪信號sn(t)進行分段濾波處理，得到新的僅保留10 Hz和30 Hz頻率分量的信號s'n(t)，信號s'n(t)的特性如圖5所示。

3)對s'n(t)進行EMD分解，所得各個IMF，如圖6所示。根據對圖6中各個IMF進行功率譜估計可知，IMF中c1和c2分別對應原始信號的30 Hz和10 Hz的頻率分量，IMF中c3和c4是由于邊界效應帶來的負效應，但其十分微弱，對原始信號的還原影響甚微。從時域看，IMF中c1和c2的信號波形比較平穩，失真不嚴重。同時，由于已經對輸入信號做了

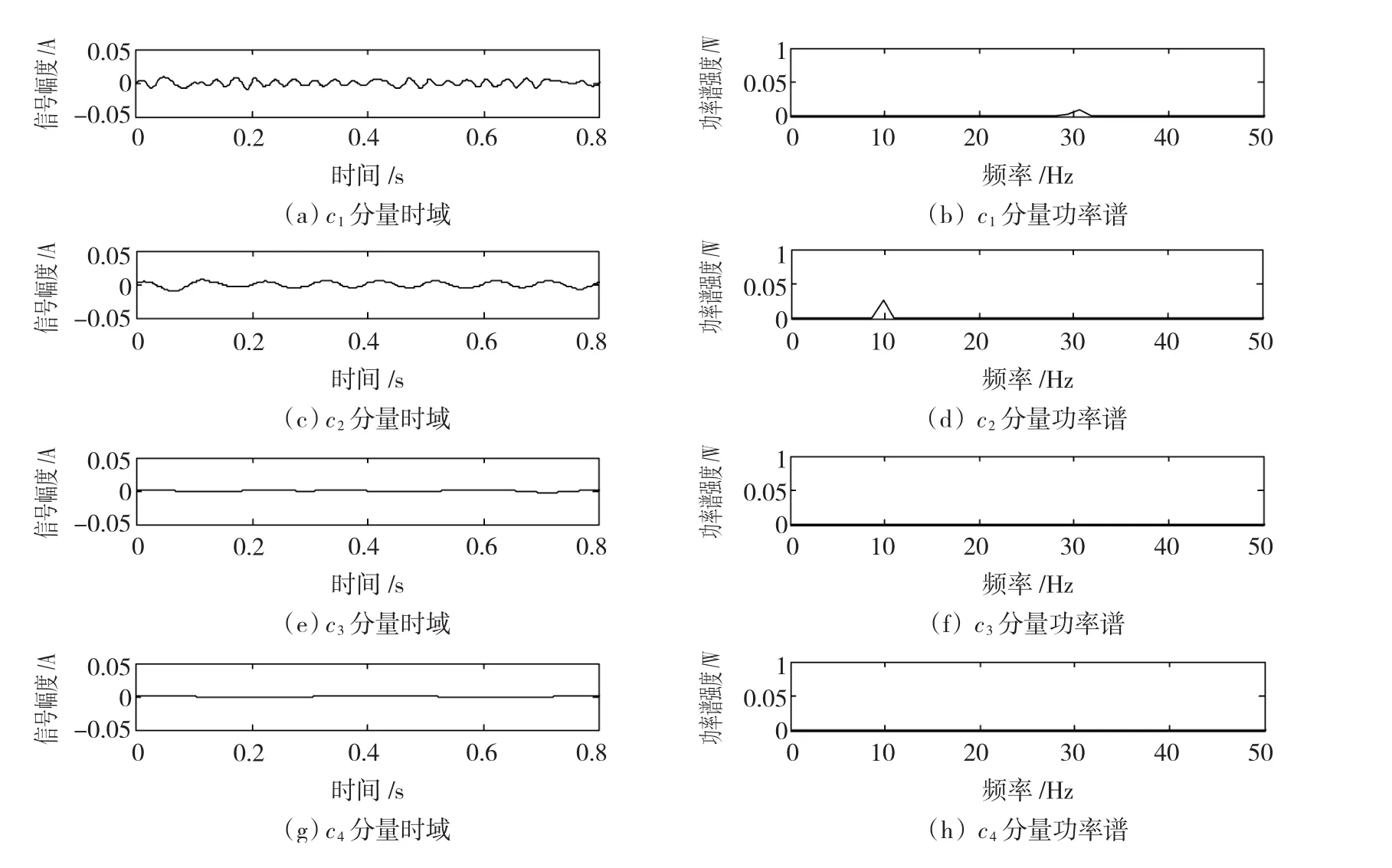
圖6 含噪信號降噪后的EMD分解圖Fig.6 Effect drawing of the de-noised signal processed by EMD system

降噪處理，使得分解出的IMF數目較少。

圖5 對原始含噪信號進行分段濾波后的信號Fig.5 Effect drawing of the de-noised signal processed by band-pass filter

4)求待測信號30 Hz和10 Hz頻率分量所應的幅度值。為了消除邊界效應對EMD分解質量的影響，對圖6中c1信號兩端各去除0.066 s的信號值得到c'1，c2信號兩端各去除0.2 s的信號值得到c'2;分別對c'1和c'2取絕對值得到c″1和c″2，分別求取c″1和c″2的局部極大值，并將其存入集合M1和M2中;分別求取集合M1和M2中數據的平均值A1=0.005 2和A2=0.005 8，A1和A2分別為c1分量和c2分量的幅度值，與真實值較好地吻合。

3 實測數據實驗

旋轉機械的轉子絕大部分應用于高轉速、高載荷環境中，這容易使軸承表面發生不均勻的磨損、腐蝕、不均勻結垢，造成機械故障。尤其是在故障的早期階段，在復雜的強噪聲背景中，故障信號相當微弱，很難檢測到故障的存在，到故障信號變得明顯后，即使檢測到故障信號的存在，也不可避免的要帶來較大的損失。圖7為現場采集到的某A型礦用鼓風機轉子振動加速度的時間序列信號sA(t)的時域和其對應的頻譜，其轉速為1 457.61 r/min，從圖中不能分析出是否含有故障信息。將該信號通入尺度變換隨機共振系統，當該信號的頻域壓縮1 000倍時，輸出信號如圖8所示，則檢測到該信號中含有49 Hz的頻率分量，該頻率為轉子轉速為24.3 Hz的2倍頻信號，推斷可能發生轉子不平衡故障。

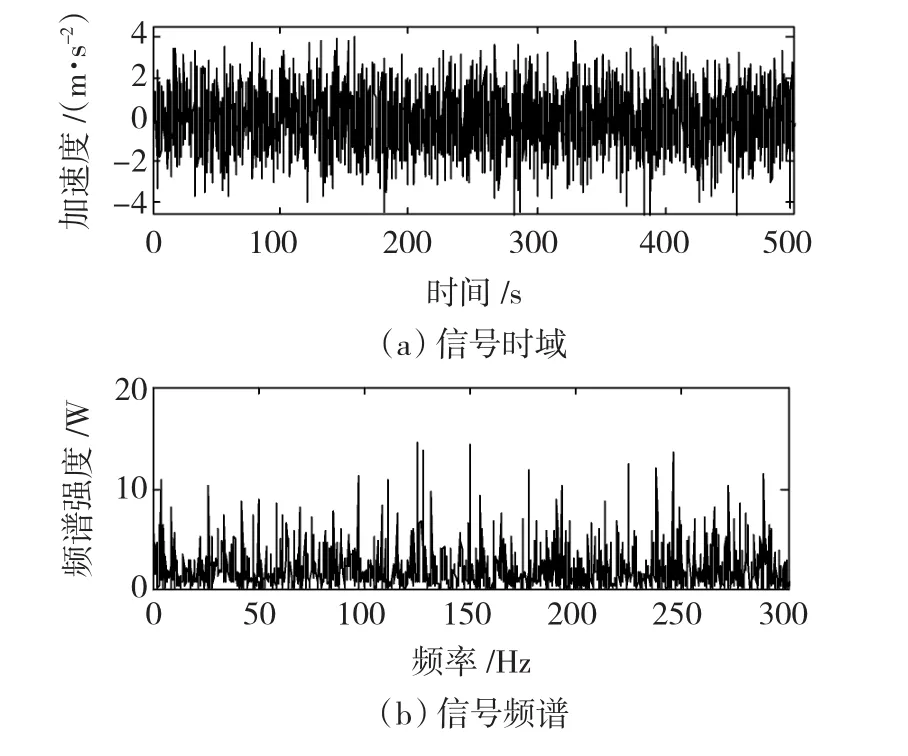
圖7 A型礦用鼓風機轉子振動加速度信號Fig.7 The vibration acceleration signal of a type A blower’s rotor

圖80 .049 Hz頻率分量共振Fig.80 .049 Hz resonance

將原始含噪信號通入中心頻率為48 Hz、帶寬為4 Hz的帶通濾波器，將濾波后的信號進行EMD分解，檢測到目標頻率信號的幅值為0.000 8 V，圖9為信號sA(t)的EMD分解所得曲線。斷定該信號幅值微弱，為噪聲擾動造成的假異常，經實際檢驗，轉子裝配合格，主軸完好無損。

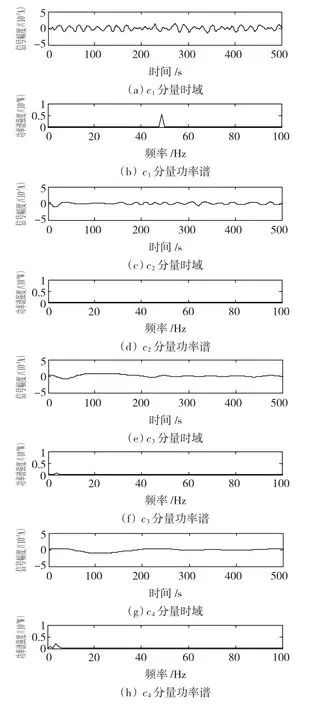
圖9 信號sA(t)的EMD分解所得曲線Fig.9 De-noised signal sA(t)processed by EMD system

圖10為現場采集到的某B型礦用鼓風機轉子振動加速度的時間序列信號sB(t)和其對應的頻譜，其轉速為984.7 r/min，從圖中不能分析出是否含有故障信息。將該信號通入尺度變換隨機共振系統，當該信號的頻域壓縮1 000倍時，輸出信號如圖11～圖13所示，則檢測到該信號中含有33 Hz、50 Hz和68 Hz的頻率分量，該頻率為轉子轉速為16.4 Hz的2倍頻、3倍頻和4倍頻信號，推斷可能發生轉子不平衡故障，將原始含噪信號通入中心頻率分別為33 Hz、49 Hz和67 Hz，帶寬為4 Hz的帶通濾波器，將濾波后的信號進行EMD分解，檢測到目標頻率信號的幅值分別為0.028 V、0.02 V和0.015 V。

圖10 某礦用鼓風機轉子振動加速度信號Fig.10 The vibration acceleration signal of a blower’s rotor

圖110 .033 Hz頻率分量共振Fig.110 .033 Hz resonance

圖120 .05 Hz頻率分量共振Fig.120 .05 Hz resonance

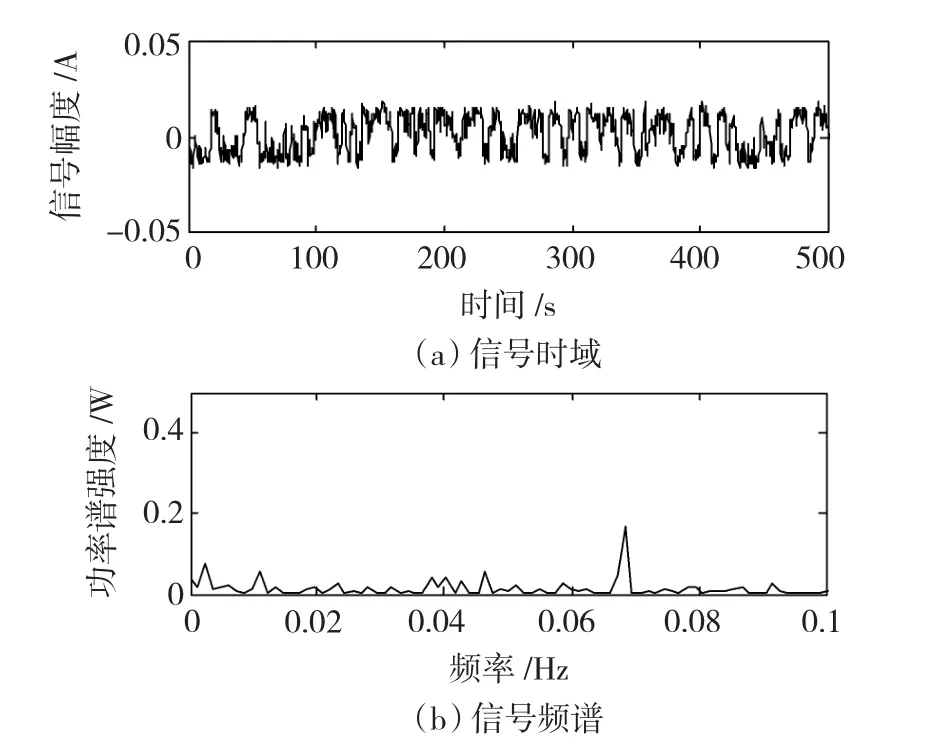
圖130 .068 Hz頻率分量共振Fig.130 .068 Hz resonance

圖14 信號sB(t)的EMD分解所得曲線Fig.14 De-noised signal sB(t)processed by EMD system

圖14為信號sB(t)的EMD分解所得曲線。斷定轉子產生了早期不平衡故障，經實際檢驗，主軸表面已經不均勻結垢，導致轉子質心和旋轉中心線之間產生了偏心距，轉子運轉時受到離心力干擾，給主軸帶來動載荷，造成轉子周期性振動。

4 結語

高載荷快速運轉的機械轉子很容易發生不平衡故障，若不能在故障發生的早期階段檢測到其存在，往往會給整套設備帶來災難性的后果。常見的微弱信號檢測方法在降低噪聲的過程中會對信號強度造成一定的壓制，這不利于微弱信號的檢測。本文提出的尺度變換隨機共振降噪下的EMD分解方法，不僅充分利用了尺度變換隨機共振系統對全頻段微弱信號自適應檢測的能力，還引入了具有根據輸入信號本征信息就能自適應分解出其對應的各個IMF分量的EMD分解技術。該方法首先將強噪聲背景下采集到的旋轉機械轉子相關信號通入尺度變換隨機共振系統，以檢測出設備是否含有故障頻率分量，并根據這里的檢測結果利用帶通濾波器對含噪信號進行降噪處理，再對處理后的信號進行EMD分解，進而根據分解得到的各個IMF分量估算出各個頻率分量對應的幅度值，根據幅度值大小進一步驗證隨機共振系統檢測到的故障信息是否準確，從而確保對轉子早期故障的精確檢測。

［1］MEHDI B，ABBAS R B.A new method for detection of rolling bearing faults based on the Local Curve Roughness approach［J］.Polish Maritime Research，2011，18(2):44－50.

［2］DONGSIK G，JAEGU K，YOUNGSU A，et al.Detection of faults in gearboxes using acoustic emission signal［J］.Journal of Mechanical Science and Technology，2011，25(5):1279－1286.

［3］FENG K，JIANG Z，HE W，et al.Rolling element bearing fault detection based on optimal antisymmetric real Laplace wavelet［J］.Measurement，2011，4(9):1582－1591.

［4］李輝，王瀚，白亮，等.改進希爾伯特—黃變換方法提取水輪機動態特征信息［J］.中國電機工程學報，2011，31(2):78－84.

LI Hui，WANG Han，BAI Liang，et al.Dynamic characteristic information extraction of hydroturbine based on improved Hilbert－Huang transform method［J］.Proceedings of the CSEE，2011，31(2):78－84.

［5］孫斌，王艷武，楊立.基于紅外測溫的異步電機軸承故障診斷［J］.電機與控制學報，2012，16(1):50－55.

SUN Bin，WANG Yanwu，YANG Li.Study of fault diagnosis of induction motor bearing based on infrared inspection［J］.Electric Machines and Control，2012，16(1):50－55.

［6］TIAGO C，BEATRIZ M G，ARMANDO V C，et al.Influence of grease rheology on thrust ball bearings friction torque［J］.Tribology International，2012，46(1):106－113.

［7］LI H，FU L，ZHENG H.Bearing fault diagnosis based on amplitude and phase map of Hermitian wavelet transform［J］.Journal of Mechanical Science and Technology，2011，25(11):2731－2740.

［8］陳果.一種改進的諧波小波及其在轉子故障診斷中的應用［J］.機械工程學報，2011，47(1):8－16.

CHEN Guo.An improved harmonic wavelet and its application to rotor faults diagnosis［J］.Journal of Mechanical Engineering，2011，47(1):8－16.

［9］陳法法，湯寶平，董紹江.基于粒子群優化LS－WSVM的旋轉機械故障診斷［J］.儀器儀表學報，2011，32(12):2747－2753.

CHEN Fafa，TANG Baoping，DONG Shaojiang.Rotating machinery fault diagnosis based on LS－WSVM with particle swarm optimization［J］.Chinese Journal of Scientific Instrument，2011，32(12):2747－2753.

［10］蘇文勝，王奉濤，朱泓，等.雙樹復小波域隱Markov樹模型降噪及在機械故障診斷中的應用［J］.振動與沖擊，2011，30(6):47－52.

SU Wensheng，WANG Fengtao，ZHU Hong，et al.Denoising method based on hidden Markov tree model indual tree complex wavelet domain and its application in mechanical fault diagnosis［J］.Journal of Vibration and Shock，2011，30(6):47－52.

［11］雷亞國.基于改進Hilbert－Huang變換的機械故障診斷［J］.機械工程學報，2011，47(5):71－77.

LEI Yaguo.Machinery fault diagnosis based on improved Hilbert－Huang transform［J］.Journal of Mechanical Engineering，2011，47(5):71－77.

［12］郝研，王太勇，萬劍，等.基于經驗模式分解和廣義維數的機械故障診斷［J］.吉林大學學報:工學版，2012，42(2):392－396.

HAO Yan，WANG Taiyong，WAN Jian，et al.Mechanical fault diagnosis based on empirical mode decomposition and generalized dimension［J］.Journal of Jilin University:Engineering and Technology Edition，2012，42(2):392－396.

［13］HE Q，WANG J，LIU Y，et al.Multiscale noise tuning of stochastic resonance for enhanced fault diagnosis in rotating machines［J］.Mechanical Systems and Signal Processing，2012，28:443－457.

［14］WANG J，ZHANG Q，XU G.Genetic stochastic resonance:a new fault diagnosis method to detect weak signals in mechanical systems［J］.Advanced Science Letters，2011，4(6－7):2508－2512.

［15］王國富，張海如，張法全，等.時頻壓縮隨機共振用于轉子故障早期檢測［J］.電機與控制學報，2011，15(6):38－44.

WANG Guofu，ZHANG Hairu，ZHANG Faquan，et al.Frequency compression of SR for detecting rotor’s incipient fault signal［J］.Electric Machines and Control，2011，15(6):38－44.

［16］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London，1998，454(12):903－995.