三相SPWM逆變器的切換模型與穩(wěn)定性分析

韓璐， 肖建， 邱存勇

(西南交通大學電氣工程學院，四川成都 610031)

0 引言

三相逆變器電路因為功率開關器件的存在，具有典型的非線性、多開關模態(tài)等特點。傳統(tǒng)的三相逆變器分析方法都是從線性系統(tǒng)的角度出發(fā)，通過平均化［1－3］、坐標變換或小信號線性化［4－6］等方法得到系統(tǒng)的近似線性化模型，并針對該模型進行穩(wěn)定性分析與控制。此類方法雖然經(jīng)典，有很強的理論支持，卻由于忽略了系統(tǒng)的某些因素，不能體現(xiàn)出三相逆變器的混雜動態(tài)特性，對系統(tǒng)分析有很大的局限性。

近年來提出的切換系統(tǒng)理論［7］可以很好地解決線性化處理為系統(tǒng)分析帶來的局限性，更精確地反映系統(tǒng)的動態(tài)混雜特性，進而有利于設計更加可靠靈活的控制器，有很好的應用前景。所謂切換系統(tǒng)［7］是指離散事件系統(tǒng)(DES)和連續(xù)變量系統(tǒng)(CVS)相混合而形成的統(tǒng)一的動態(tài)系統(tǒng)。由于功率開關器件的存在，大部分的電力電子裝置都是典型的切換系統(tǒng)。文獻［8］基于切換系統(tǒng)理論構建了DC/DC變換器的切換系統(tǒng)模型，并基于該模型提出DC/DC電路的參數(shù)辨識方法。文獻［9－10］從切換的角度提出了DC/DC變換器的建模與控制新方法。但是上述方法僅限于由兩個子系統(tǒng)組成的切換系統(tǒng)，對于更復雜的電力電子電路，隨著開關模式的豐富，子系統(tǒng)大大增加，該方法便不再適用。文獻［11］針對復雜電路，在切換理論基礎上建立了三相變流器的切換系統(tǒng)模型，并引入等時切換系統(tǒng)的穩(wěn)定性判據(jù)進行穩(wěn)定性分析，該方法對研究普遍的電力電子裝置有一定的參考價值。

三相SPWM逆變器屬于三相變流器的一種，是典型的周期切換系統(tǒng)。基于文獻［12］提出的周期切換系統(tǒng)漸近穩(wěn)定的充要條件，文獻［11］對三相變流器切換過程的穩(wěn)定性進行了初步分析，但是由于系統(tǒng)模型是在等時周期切換這一特殊情況下建立的，在穩(wěn)定性分析過程中存在一定的局限性。本文在此基礎上進行改進，以周期切換系統(tǒng)理論為基礎，從三相SPWM逆變器的建模與穩(wěn)定性分析兩個方面分別進行設計。首先，根據(jù)SPWM調制特性，將一個工頻周期按三相母線電壓大小劃分為6個區(qū)間，分別得到切換子系統(tǒng)與對應的周期切換規(guī)則，即三相SPWM逆變器的周期切換模型。在系統(tǒng)穩(wěn)定性分析方面，本文通過將切換子系統(tǒng)滯留時間當作不確定參數(shù)，將三相SPWM逆變器的切換模型轉換為多胞型模型，并利用多胞型模型與周期切換系統(tǒng)的穩(wěn)定性等價關系實現(xiàn)對三相逆變器切換過程的穩(wěn)定性判斷。為了降低保守性，多胞型模型的穩(wěn)定性分析中利用參數(shù)依賴型Lyapunov函數(shù)。

1 三相SPWM逆變器切換動態(tài)模型

1.1 子系統(tǒng)模型

圖1為三相SPWM逆變器［4］的拓撲結構圖，它是基于電壓型變流器(VSC)結構的功率逆變電路，其工作原理是通過SPWM(正弦波脈寬調制)技術控制功率開關器件S1～S6的關斷，使得輸出的電壓或電流為標準正弦波，達到逆變電源的要求。因為功率開關器件的存在，三相SPWM逆變器為典型的切換系統(tǒng)。

圖1 三相SPWM逆變器的拓撲結構圖Fig.1 Topology of three-phase SPWM inverter

為分析方便，首先定義單極性二值邏輯開關函數(shù)sk為

將三相VSC功率開關管損耗Rs同交流側負載電阻Rl合并，且令R=Rl+Rs，采用基爾霍夫電壓定律建立三相電壓型逆變器的a相回路方程為

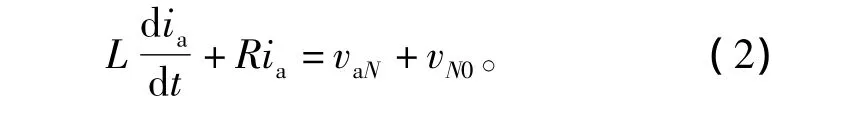
其中vaN=vdcsa。

同理可得b相、c相回路方程為

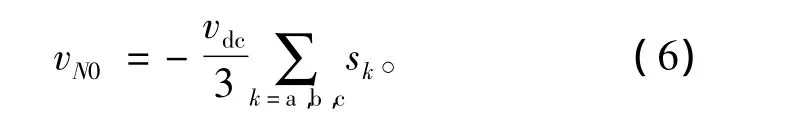
另外，對直流側電容正極節(jié)點處采用基爾霍夫電流定律，得

考慮三相對稱系統(tǒng)，則

聯(lián)立式(2)～式(5)，得

令狀態(tài)變量x=［ia，ib，ic，vdc］T，則采用單極性二值邏輯開關函數(shù)描述的三相電壓型逆變器的一般狀態(tài)方程可以表示為

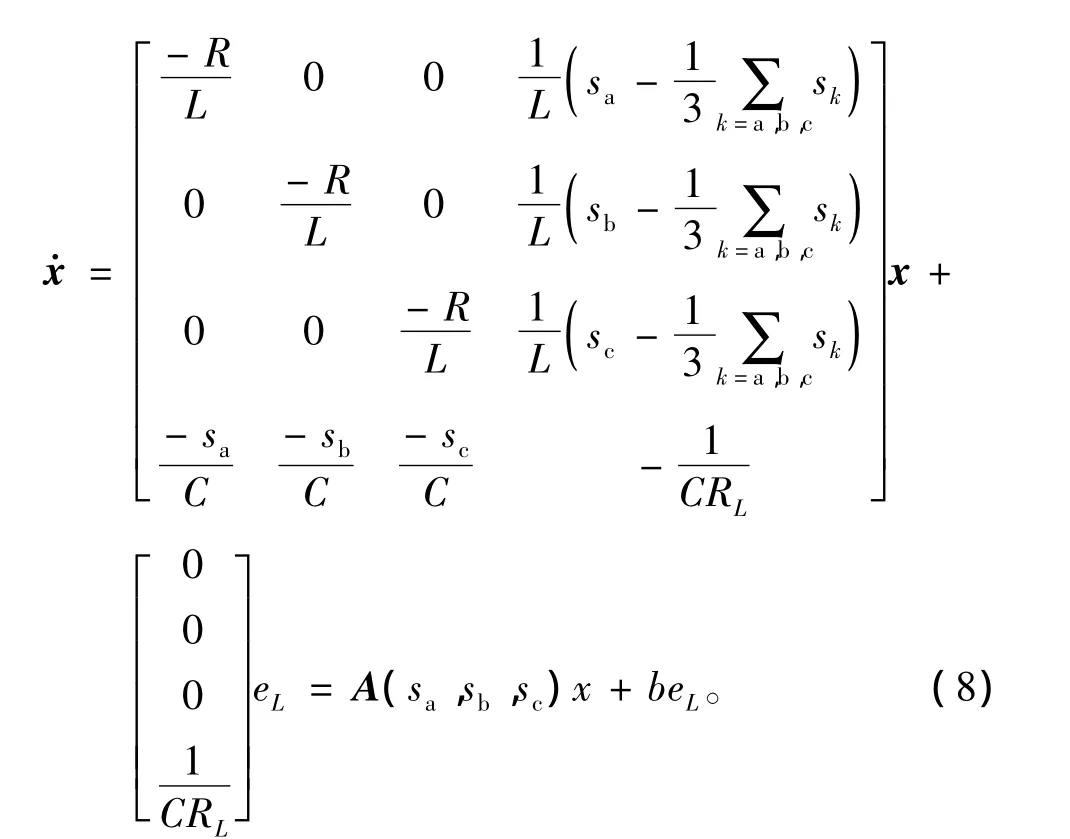
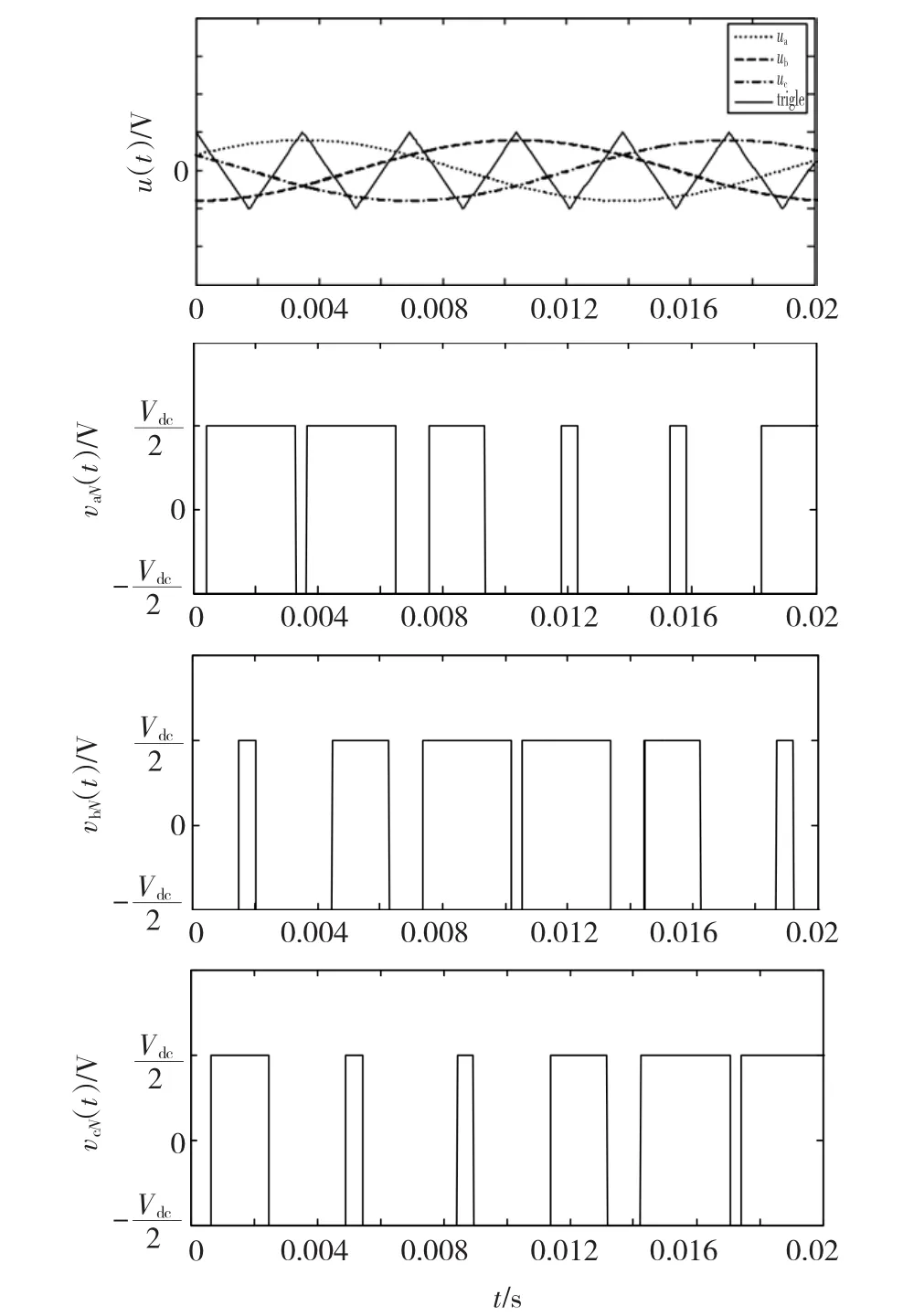
圖2 SPWM波形產(chǎn)生原理Fig.2 Schematic diagram of SPWM pulses generation

其中:sa、sb、sc的值不同對應不同的系統(tǒng)矩陣。根據(jù)式(1)，sa、sa、sc組成系統(tǒng)的8種開關模態(tài)，如表1所示。

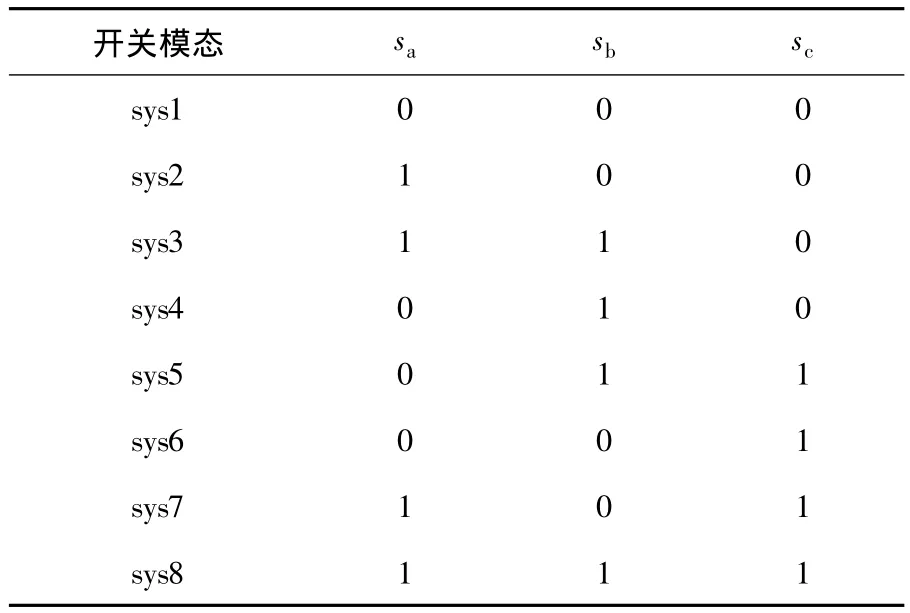
表1 SPWM逆變器的8種開關模態(tài)Table 1 Different switching modes of SPWM inverter

SPWM逆變器的開關模態(tài)即為系統(tǒng)的切換子系統(tǒng)，將表1中sa、sb、sc的值代入式(8)，可以得到三相電壓型逆變器的切換子系統(tǒng)模型

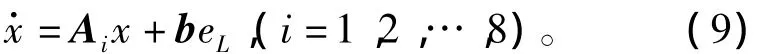
1.2 切換規(guī)則

線性切換系統(tǒng)的模型由兩部分組成，分別是線性子系統(tǒng)以及切換規(guī)則。SPWM控制方式是一種特殊的切換規(guī)則，它是對逆變電路開關器件的通斷進行控制，使得輸出端得到一系列幅值相等而寬度不相等的脈沖，用這些脈沖來代替正弦波或其它需要的波形。SPWM調制原理如圖2所示。

文獻［11］提出的SPWM逆變器模型中，切換規(guī)則被處理為8個子系統(tǒng)依次切換的等時周期切換，這種處理方式存在一定的局限性。根據(jù)SPWM調制原理，SPWM逆變器的切換規(guī)則應該是受三相母線電壓大小影響的周期切換，切換周期為工頻周期。

為了用數(shù)學方法歸納SPWM這種特殊的切換規(guī)則，將一個工頻周期內(nèi)的調制過程按三相正弦調制電壓的交點從左向右分為ua＞uc＞ub，ua＞ub＞uc，ub＞ua＞uc，ub＞uc＞ua，uc＞ub＞ua和uc＞ua＞ub六個區(qū)間，由于三相對稱性，每個區(qū)間的時間取值為T/6，記為Ts。下面以ua＞uc＞ub為例詳細介紹系統(tǒng)的切換規(guī)則，為了分析方便，假設SPWM調制過程中三角載波周期也為T 。

當母線電壓滿足ua＞uc＞ub時，三相共載波SPWM控制方式如圖3所示。

圖3 三相共載波PWM調制原理Fig.3 Three-phase PWM pulses generation with common carrier wave

這種控制方式是將三相作為一個整體，在同一個周期Ts中同時對a，b，c三相進行調制。圖中通過SPWM調制過程產(chǎn)生了7個時間區(qū)域，對應著不同的子系統(tǒng)模態(tài)，三相調制電壓對應不同的占空比，分別是η1，η2和η3。因為7種子系統(tǒng)模態(tài)中有些模態(tài)存在逆變過程的重復，可以看作冗余模態(tài)，所以對圖3的脈寬重新排列順序得到三相共載波SPWM波形，如圖4所示。

圖4 重排后的SPWM波形Fig.4 Three-phase SPWM pulses after rearrangement

由圖4可以看出，在同一開關周期Ts中，經(jīng)過SPWM調制只產(chǎn)生四個時間區(qū)間d1，d2，d3和d4。這4個時間區(qū)間分別對應表1中的子系統(tǒng)sys1，sys2，sys7，sys8，將相應sa、sb、sc的值代入式(8)，可以得到子系統(tǒng)矩陣A1，A2，A7，A8。其余五個區(qū)間的分析類似，不再重復。值得指出，由于三相對稱性和區(qū)間選取的平均原則，每個區(qū)間對應子系統(tǒng)的滯留時間是相等的。從以上的分析得出三相SPWM逆變器的周期切換規(guī)則如圖5所示。

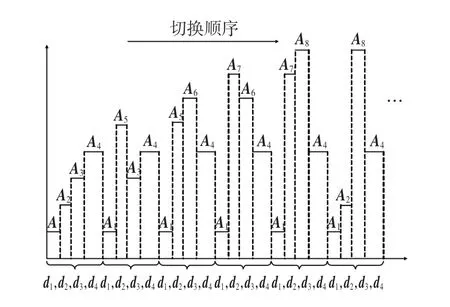
圖5 三相SPWM逆變器的周期切換規(guī)則Fig.5 Periodic switching rules of three-phase SPWM inverter

由于SPWM調制原理遵循脈寬調制原則，圖5中每個子系統(tǒng)的滯留時間d1，d2，d3，d4可理解為正弦波幅值對應的等效脈寬，即遵循正弦波變化規(guī)律。從這一角度可以得到子系統(tǒng)滯留時間d1，d2，d3，d4的實際數(shù)值。

值得注意的是，三角波載波周期不同，所得到的切換規(guī)則是不同的，對應的子系統(tǒng)滯留時間也是不同的，但是均可通過以上方法歸納出系統(tǒng)切換規(guī)則。

2 三相SPWM逆變器的穩(wěn)定性分析

三相SPWM逆變器為典型的線性仿射周期切換系統(tǒng)［11］。考慮到其不同開關組合對應的子系統(tǒng)模型(9)為線性時不變的，且仿射項beL為恒定常數(shù)，不受切換過程的影響，三相SPWM逆變器的穩(wěn)定性分析可以簡化為對線性自治周期切換系統(tǒng)=Aix的穩(wěn)定性判斷，進而可以利用下述引理。

引理1［12］切換系統(tǒng)=Aix，i=1，2，…，m通過周期切換規(guī)則后漸近穩(wěn)定的充要條件是系統(tǒng)αiAix漸近穩(wěn)定，其中αi是正整數(shù)且滿足τi=αiτ，i=1，2，…，m，τi為周期切換下的子系統(tǒng)滯留時間，τ為等時周期切換下的子系統(tǒng)滯留時間。

文獻［11］曾引用過該周期切換系統(tǒng)的穩(wěn)定性判據(jù)對三相變流器進行穩(wěn)定性分析，但是整個分析過程均建立在等時周期切換這一特殊情況下，即假設 αi=1，i=1，2，…，m，有一定的局限性。在此基礎上做以改進，通過將切換子系統(tǒng)滯留時間作為不確定參數(shù)，將三相SPWM逆變器的切換模型轉換成多胞型模型［13］，進而利用引理1實現(xiàn)對三相逆變器切換過程的穩(wěn)定性判斷。為了降低保守性，多胞型模型的穩(wěn)定性分析中利用參數(shù)依賴型Lyapunov函數(shù)，具體步驟如下。

由于子系統(tǒng)滯留時間隨著三角波載波周期的不同而變化，逆變器各子系統(tǒng)的滯留時間可以看作不確定參數(shù)(這些參數(shù)均可測量)，則SPWM逆變器的自治切換動態(tài)模型轉換成參數(shù)不確定多胞型模型為

之后利用魯棒控制的相關理論對系統(tǒng)(10)進行穩(wěn)定性分析。值得指出的是，對于這種參數(shù)不確定系統(tǒng)的魯棒控制理論早已成熟，最常用的二次穩(wěn)定性判據(jù)［13］為公共Lyapunov判據(jù)，它要求有一個對所有的不確定參數(shù)都適用的Lyapunov矩陣，所以在簡單易設計的同時存在很大的保守性。為了避免該保守性，本文采用參數(shù)依賴的Lyapunov矩陣［13－16］對三相SPWM逆變器的多胞模型進行穩(wěn)定性分析。參數(shù)依賴型Lyapunov穩(wěn)定性判據(jù)如定義1所示。

定義1稱具有式(10)系統(tǒng)矩陣的多胞模型為二次穩(wěn)定［13］的，當且僅當存在一組對稱矩陣Pi，i=1，2，…，8，使得對所有的不確定參數(shù) δ∈Δ，

成立。其中矩陣P(δ)是不確定參數(shù)δi的一個多胞函數(shù)。

該定義中提出的線性矩陣不等式判據(jù)，可以利用Matlab中的魯棒控制工具箱LMI來求解。LMI工具箱提供了檢驗由多胞型模型所描述的不確定系統(tǒng)二次穩(wěn)定性的函數(shù)pdlstab［13］，其一般表達式為

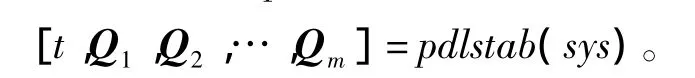
其中，sys為多胞型模型的系統(tǒng)矩陣，且函數(shù)輸出為參數(shù)依賴矩陣

該函數(shù)指出，如果t＜0，則所考慮的系統(tǒng)為多胞二次穩(wěn)定的，且V(x，δ)=xTQ－1(δ)x定義了一個參數(shù)依賴的Lyapunov函數(shù)。

二次穩(wěn)定的系統(tǒng)必然漸近穩(wěn)定。利用參數(shù)依賴型Lyapunov穩(wěn)定性判據(jù)和LMI工具箱函數(shù)pdlstab可以很容易地從子系統(tǒng)矩陣A1～A8的數(shù)值中判斷出三相SPWM逆變器的多胞不確定系統(tǒng)模型(10)為漸近穩(wěn)定的，進而根據(jù)引理1得到經(jīng)周期切換序列下的原切換系統(tǒng)(9)穩(wěn)定。

3 數(shù)字仿真

為了驗證本文構造的逆變器模型以及穩(wěn)定性分析方法的正確性，本節(jié)在Matlab軟件環(huán)境下進行了系統(tǒng)仿真。假設R/L=2 500，1/L=125，1/C=100，1/CRL=5，eL=400 V，切換周期T=0.02 s，載波頻率fs=300 Hz，子系統(tǒng)滯留時間分別為d1=0.000 65 s，d2=0.001 16 s，d3=0.001 16 s，d4=0.000 36 s。令系統(tǒng)初始狀態(tài)x0=(20，20，20，300)T，則三相逆變器切換子系統(tǒng)(9)通過圖5周期切換規(guī)則后的系統(tǒng)狀態(tài)軌跡如圖6所示。

系統(tǒng)的狀態(tài)軌跡體現(xiàn)了一定的切換特征。由圖6可知，在8個子系統(tǒng)以工頻為周期做周期切換的情況下，系統(tǒng)狀態(tài)各分量隨時間的變化曲線是連續(xù)的且隨時間的增大始終收斂于有限區(qū)域內(nèi)。該仿真波形體現(xiàn)了切換系統(tǒng)的穩(wěn)定性，與之前的分析結果共同證實了周期切換模型與系統(tǒng)等效多胞型模型的穩(wěn)定等價性，進而說明了本文關于三相SPWM逆變器的穩(wěn)定性分析方法是正確的。

圖6 周期切換規(guī)則下逆變器的狀態(tài)軌跡Fig.6 State movement track of inverter under periodic switching series

同時，為了體現(xiàn)本文建立的逆變器切換模型較傳統(tǒng)的線性近似化模型的優(yōu)越性，分別對兩種模型下輸出的a相電壓波形進行比較分析，如圖7所示。

由圖7的對比波形可以看出，在相同載波頻率下，所建立的逆變器切換模型輸出的a相電壓波形平滑均勻，抗干擾能力強，較傳統(tǒng)的小信號線性化模型輸出的電壓波形更接近于指令正弦波，更滿足三相SPWM逆變器的工作要求。

圖7 不同模型下的a相輸出電壓波形Fig.7 Output a-phase voltage waveforms of different models

以上仿真結果只給出了三相SPWM逆變器切換模型輸出的a相穩(wěn)態(tài)電壓波形。為了更全面地體現(xiàn)切換系統(tǒng)模型的抗干擾能力，本節(jié)還給出了擾動情況下a相輸出電壓的特性分析。假設在t=0.1 s時刻，直流電壓eL由400 V突變到800 V，a相輸出電壓的暫態(tài)波形如圖8所示。

圖8 擾動情況下a相輸出電壓波形Fig.8 Output a-phase voltage waveform under disturbance

圖8清晰地呈現(xiàn)出在擾動產(chǎn)生瞬間，三相SPWM逆變器切換模型輸出的a相暫態(tài)電壓波形平滑過渡，且隨著時間的推移逐漸穩(wěn)定在新的指令值上。值得注意的是，載波頻率越高，輸出的電壓波形越接近正弦波。本節(jié)考慮仿真時效性采用了較低的載波頻率，工程中只要適當提高載波頻率，該切換模型可以達到更好的效果。

4 結論

由SPWM調制原理可知，三相逆變器是典型的周期切換系統(tǒng)。本文以周期切換系統(tǒng)理論為基礎，從三相SPWM逆變器的建模與穩(wěn)定性分析兩個方面分別進行設計。在系統(tǒng)建模方面，本文將一個工頻周期按三相母線電壓大小劃分為6個區(qū)間，分別得到切換子系統(tǒng)與切換規(guī)則，即三相SPWM逆變器的周期切換模型。這樣得到的切換規(guī)則較文獻［11］提出的8個子系統(tǒng)依次切換的等時切換規(guī)則更符合實際系統(tǒng)的動態(tài)需要。在系統(tǒng)穩(wěn)定性分析方面，本文在文獻［11］的關于等時周期切換方法的基礎上加以改進，通過將切換子系統(tǒng)滯留時間作為不確定參數(shù)，利用多胞型模型的穩(wěn)定性判定方法來判斷三相SPWM切換系統(tǒng)的穩(wěn)定性。為了避免保守性，在多胞型模型的穩(wěn)定性分析中采用了參數(shù)依賴型Lyapunov函數(shù)。最后，在Matlab軟件環(huán)境下的仿真結果驗證了本文關于三相逆變器切換模型以及穩(wěn)定性分析方法的正確性。值得指出的是，本文提出的基于切換系統(tǒng)理論的系統(tǒng)建模與穩(wěn)定性分析方法可以推廣到具有周期切換特性的其他PWM變換器的研究中，有一定的普遍意義。

［1］Middlebrook R D.Small-signal modeling of pulse-width modulated switched-mode power converters［J］.Proceedings of the IEEE，1988，76(4):343－354.

［2］王立建，王明渝，劉洋.一種新型的電壓源逆變器并聯(lián)控制策略［J］.電力系統(tǒng)保護與控制，2012，40(2):51－55.

WANG Lijian，WANG Mingyu，LIU Yang.A novel control strategy for parallel operation of voltage source inverter［J］.Power System Protection and Control，2012，40(2):51－55.

［3］董鋒斌，皇金鋒.一種三相SPWM逆變器的建模和控制方法［J］.電機與控制學報，2010，14(8):87－92.

DONG Fengbin，HUANG Jinfeng，ZHONG Yanru.A modeling and controlling approach of three-phase SPWM inverter［J］.Electric Machines and Control，2010，14(8):87－92.

［4］張崇巍，張興，PWM整流器及其控制［M］.北京:機械工業(yè)出版社，2002.

［5］Ye Y，Kazerani M，Quintana V H.A novel modeling and control method for three phase PWM converters［C］//IEEE 32nd Annual Power Electronics Specialists Conference，June 17－21，2001，Vancouver，BC，Canada，2001:102－107.

［6］李軍徽，朱昱，嚴干貴.儲能系統(tǒng)控制策略及主電路參數(shù)設計的研究［J］.電力系統(tǒng)保護與控制，2012，40(7):7－12.

LI Junhui，ZHU Yu，YAN Gangui.Research on the control strategy and the design of main circuit parameters of energy storage system［J］.Power System Protection and Control，2012，40(7):7－12.

［7］HAI Lin，PANOS J.Antsaklis.Stability and stabilizability of switched linear systems:A survey of recent results［J］.IEEE Transactions on Automatic Control，2009，54(2):308－322.

［8］馬皓，毛興云.基于混雜系統(tǒng)模型的DC/DC電力電子電路參數(shù)辨識［J］.中國電機工程學報，2005，25(10):50－54.

MA Hao，MAO Xinyun.Parameter identification of DC/DC power electronic circuits based on hybrid system model［J］.Proceedings of the CSEE，2005，25(10):50－54.

［9］陸益民，張波.DC/DC變換器的切換仿射線性系統(tǒng)模型及控制［J］.中國電機工程學報，2008，28(15):16－22.

LU Yimin，ZHANG Bo.Switched affine systems modeling and control of DC/DC converters［J］.Proceedings of the CSEE，2008，28(15):16－22.

［10］高明遠.雙向DC/DC變換器基于切換系統(tǒng)的建模與儲能控制［J］.電力系統(tǒng)保護與控制，2012，40(3):129－134.

GAO Mingyuan.Modeling and energy storage control for bi-directional DC/DC converter based on switching system［J］.Power System Protection and Control，2012，40(3):129－134.

［11］李瓊林，劉會金.基于切換系統(tǒng)理論的三相變流器建模及其穩(wěn)定性分析［J］.電工技術學報，2009，24(11):89－95.

LI Qionglin，LIU Huijin.Modeling and stability analysis of threephase converter based on switching system theory［J］.Transactions of China Electro Technical Society，2009，24(11):89－95.

［12］高立群，景立.線性切換系統(tǒng)經(jīng)周期切換漸近穩(wěn)定性研究［J］.控制與決策，2005，20(5):541－544.

GAO Liqun，JING Li.Asymptotical stabilization of switched linear system via periodic switching sequences［J］.Control and Decision，2005，20(5):541－544.

［13］俞立.魯棒控制—線性矩陣不等式處理方法［M］.北京:清華大學出版社，2002.

［14］ZHANG Lixian，WANG Changhong.Stability and stabilization of a class of multimode linear discrete-time systems with polytopic uncertainties［J］.IEEE Transactions on Industrial Electronics，2009，56(9):3684－3692.

［15］ZHAI Guisheng，LIN Hai.Quadratic stabilizability of switched linear systems with polytopic uncertainties［J］.International Journal of Control，2003，76(7):747－753.

［16］Pascal Gahinet，Arkadii Nemirovskii.LMI control toolbox［C］//Proceedings of the IEEE Conference on Decision and Control，March 27－29，1994，York，England，1994:2038－2041.