PMSM伺服系統速度環PI控制器參數自整定及優化

肖啟明， 楊明， 劉可述， 賈下跖， 秦潔

(1.重慶三峽學院 機械工程學院，重慶 400410;2.哈爾濱工業大學電氣工程系，黑龍江 哈爾濱 150001;3.中船重工集團第七○七研究所九江分部，江西九江 332000;4.中電投江西核電有限公司，江西九江 332000)

0 引言

在伺服系統中，系統參數變化(如負載轉矩或轉動慣量的變化)可能會嚴重影響系統的控制效果，導致系統動態響應性能惡化甚至產生振蕩［1］。為了保證在伺服系統參數發生變化后，伺服系統仍具有良好的動靜態性能，需對控制器參數進行自整定。

按照工作機理可以將PI參數自整定方法分為兩大類:基于模型的PI參數自整定和基于規則的PI參數自整定［2－5］。基于模型的PI參數自整定是基于系統的精確數學模型和一些假設條件，根據系統的響應性能指標按傳統控制理論對PI參數進行直接配置，如Ziegler－Nichols(Z－N)整定法、繼電器反饋整定法等。文獻［6］提出了一種改進型Z－N整定法，其以提高系統瞬態響應性能為依據，根據系統當前過程變化趨勢對系統速度環PI參數進行整定;文獻［7］則以系統數學模型為基礎，通過系統期望截止頻率和相角裕度來對控制參數直接配置。這類方法依賴系統模型的建模精度和假設條件的合理行，且過于復雜。基于規則的PI參數自整定則是以伺服系統的實際控制效果作為依據，通過對系統階躍響應進行評價的評價函數和參數優化準則來獲得PI參數最優值。文獻［8］提出了一種將坐標輪換法和評價函數IITAE結合的算法來整定PI控制參數。這類方法的難點在于參數優化準則的確定以及存在優化過程長的問題。

本文提出了一種將基于模型和規則的PI參數自整定思想相結合的參數自整定策略。首先在系統精確數學模型的基礎上利用系統的開環截止頻率和相角裕度等頻域性能指標來獲得一組PI參數(KpsJ，KisJ)，然后以ITAE為評價函數和參數(KpsJ，KisJ)為初始值，利用二自由度迭代法在微小范圍內通過對不同PI參數下系統階躍響應進行評價，根據最小ITAE值尋找系統的最佳PI參數(KpsJ(n)，KisJ(n))，從而使系統獲得最佳的動靜態性能。

1 基于頻域法的速度環PI參數設計

因為在實際系統中，電流環的帶寬遠遠高于速度環的期望截止頻率，所以可以將電流環的閉環傳遞函數等效為單位增益的慣性環節。則速度環的結構框圖如圖1所示。

其中，速度調節器采用PI控制器，其傳遞函數為

式中，Kps、Kis分別為速度PI控制器的比例增益、積分時間常數。

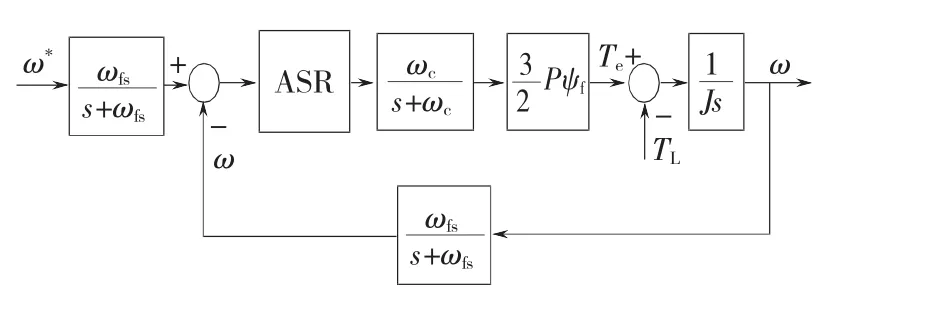
圖1 速度環結構控制框圖Fig.1 Block diagram for speed loop

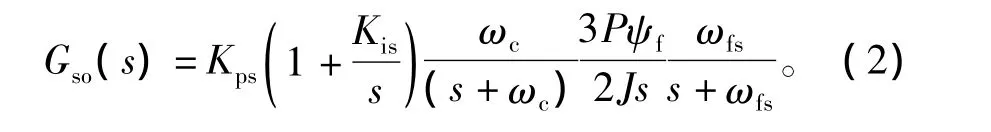
式中:ωc為電流環帶寬;ωfs為速度檢測一階低通濾波器的截止頻率;P為極對數;ψf為永磁體磁鏈;J為轉動慣量。

設定速度環開環截止頻率和相角裕度分別為ωsc、ψsm，則速度環開環傳遞函數應滿足式(3)和式(4)所示的幅相關系。

相頻關系:

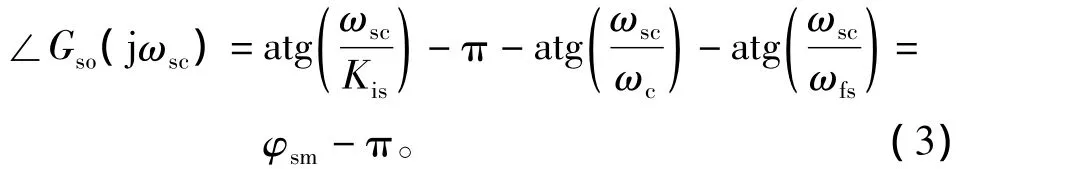
由圖1可得速度環開環傳遞函數為

幅頻關系:

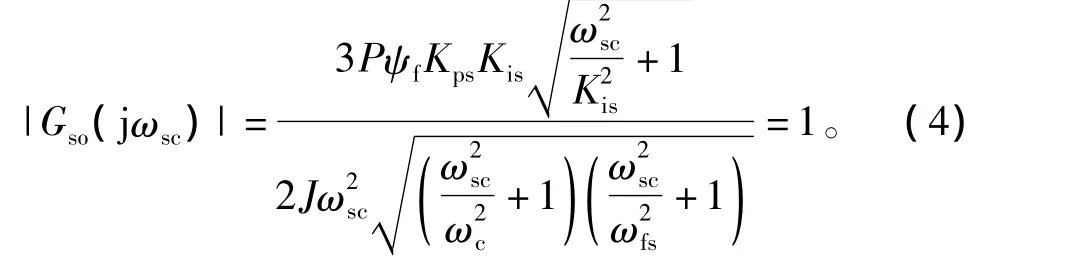
通過上述幅相關系可求解出速度PI控制器參數:

速度PI控制器比例增益

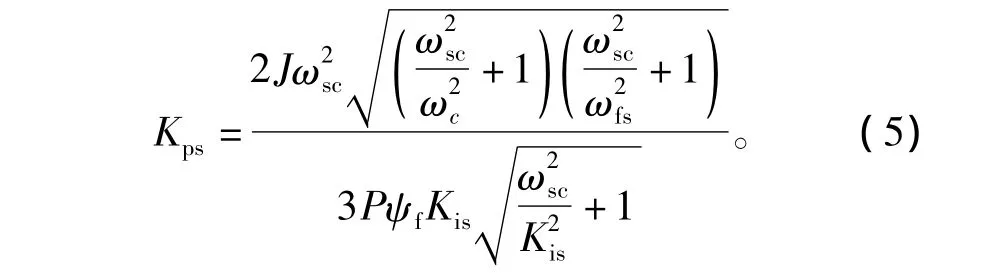
速度PI控制器積分時間常數

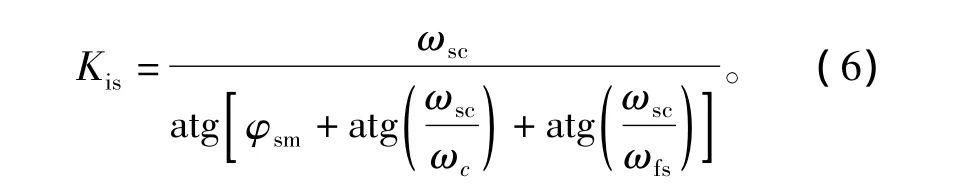
在參數設計過程中，為了降低算法的復雜性而引入控制系數

在截止頻率ωsc處，PI控制器對整個伺服系統所提供的滯后相角θPI由系數u決定，

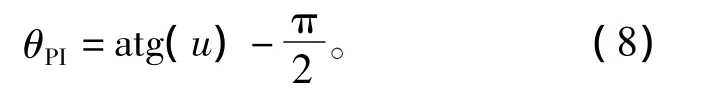
當系數u取值不同時，PI控制器對伺服系統造成的相角滯后不同，進而也就決定了系統的相角裕度不同。為了使系統在截止頻率處相角裕度達到最大值，控制系數u應滿足

由式(5)和式(7)聯立可求解出速度PI控制器參數關于控制系數u的表達式

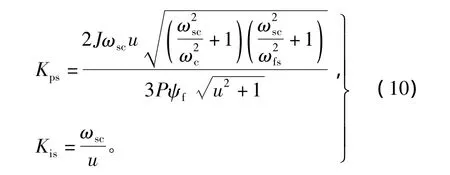
在伺服系統中，若滿足電流環帶寬ωc遠遠高于速度環截止頻率ωsc，速度檢測低通濾波器的截止頻率ωfs遠遠高于速度環截止頻率ωsc，即有

成立。

可以得到簡化后的速度環PI控制參數為

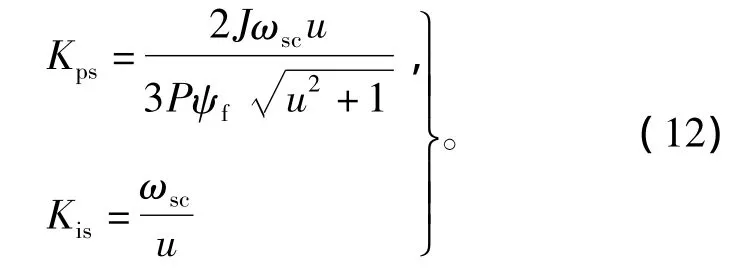
圖3 所示是二自由度迭代整定法參數優化流程圖。具體優化過程如下:

為了使經過PI控制器校正后的系統具有較大的相角裕度，本文中選取控制系數u為5，則速度環PI控制參數最終為

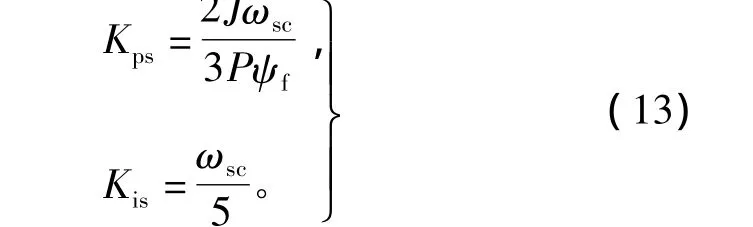
由于文獻［9－10］提出了簡單有效、辨識精確度高的負載轉動慣量辨識算法，本文將直接引用其成果。通過式(14)和辨識到的負載轉動慣量比(負載慣量與電機本體慣量的比值)KJ可獲得對應轉動慣量的速度環PI控制器參數。

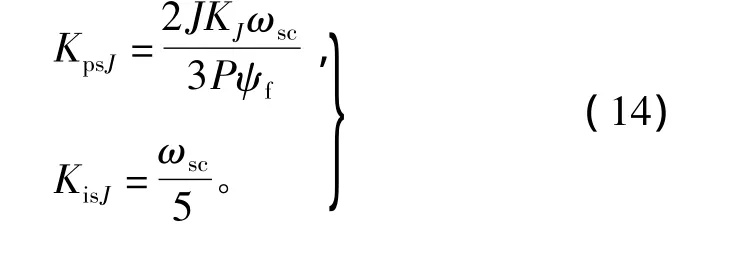
2 基于二自由度迭代整定法的速度環PI參數優化

由于在實際系統中，不可避免的存在轉矩脈動、摩擦和系統離散化等影響，基于頻域法設計的速度環PI參數不一定能使伺服系統具有最佳控制性能，所以需對設計的參數進一步優化。

所提出的二自由度迭代整定法以ITAE為評價函數和頻域法設計的速度環PI參數(KpsJ，KisJ)為初始值，在初始值的附近通過對不同PI參數下系統階躍響應進行評價，根據最小ITAE值尋找系統的最佳PI控制器參數。圖2所示是基于二自由度迭代整定法的伺服系統參數整定框圖。

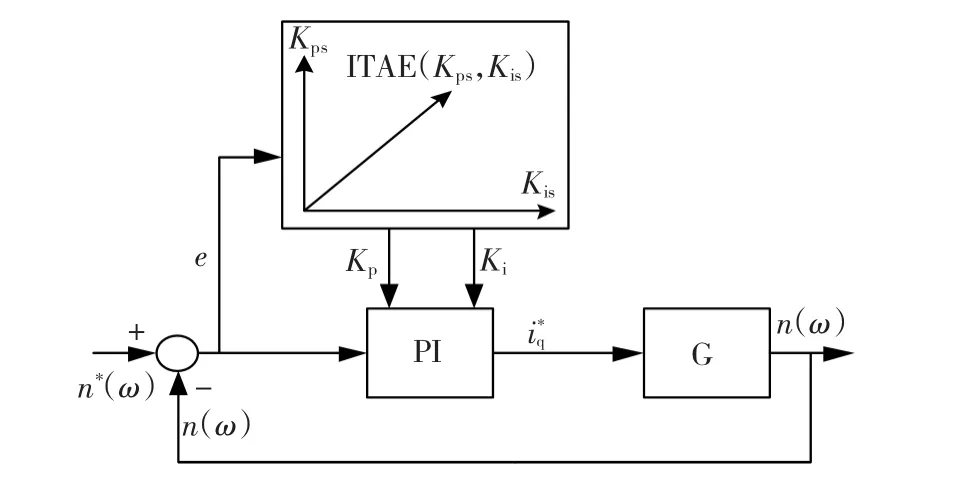
圖2 二自由度迭代整定法的伺服系統參數整定框圖Fig.2 Block diagram for two-degrees-freedom iteration method

1)以頻域法設計的PI參數(KpsJ，KisJ)為參數優化的基點，(ΔKps，ΔKis)為參數增量，確定一組測試參數(Kps，Kis);

2)給定如圖4所示的速度階躍指令，計算不同測試參數下系統性能響應的評價函數值FITAE，其中

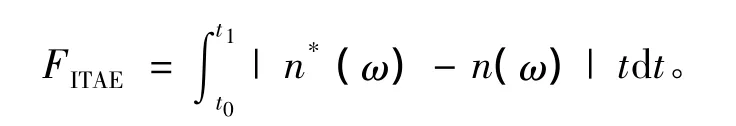
3)將最小評價函數值FITAEmin對應的參數作為新的測試基點(Kps(n)，Kis(n))并確定新的測試參數，重復2)、3)兩步的測試;

4)直到兩組測試參數的基點相同，即滿足式(15)時，則認為迭代過程完成，優化參數為(Kps(n)，Kis(n))。

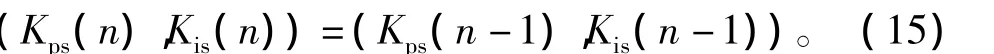
其中，步驟1)中的測試參數按下式確定

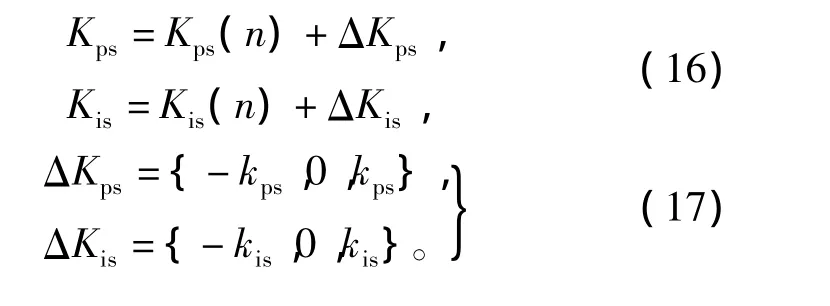
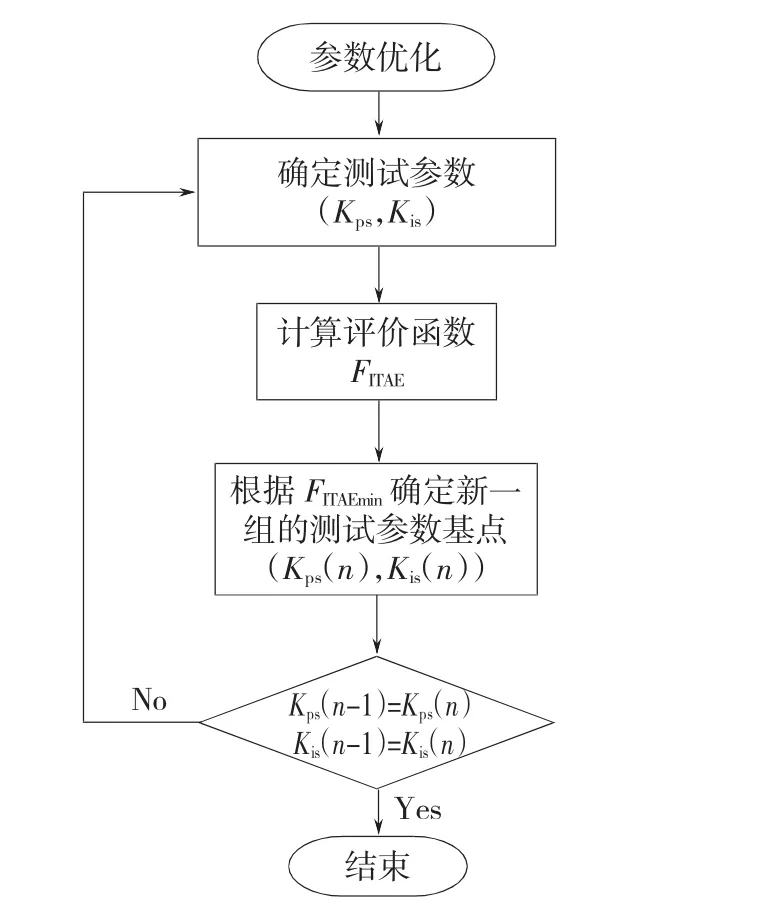
圖3 二自由度迭代整定法參數優化流程圖Fig.3 Parameters optimization flow chart for 2DOF

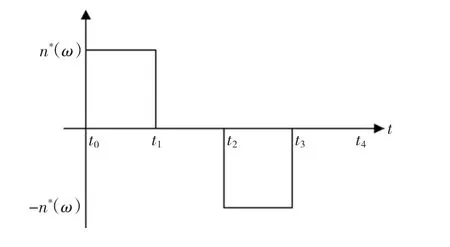
圖4 速度階躍周期指令Fig.4 Speed step instruction

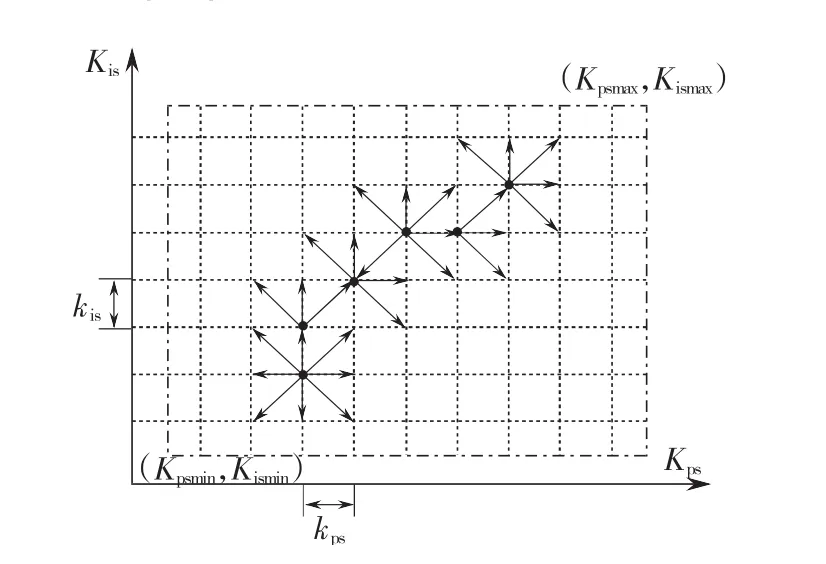
圖5 二自由度迭代整定法的PI參數優化軌跡Fig.5 PI parameters optimization trajectory of 2DOF

3 實驗結果與分析

實驗平臺采用的永磁同步交流伺服系統主要性進

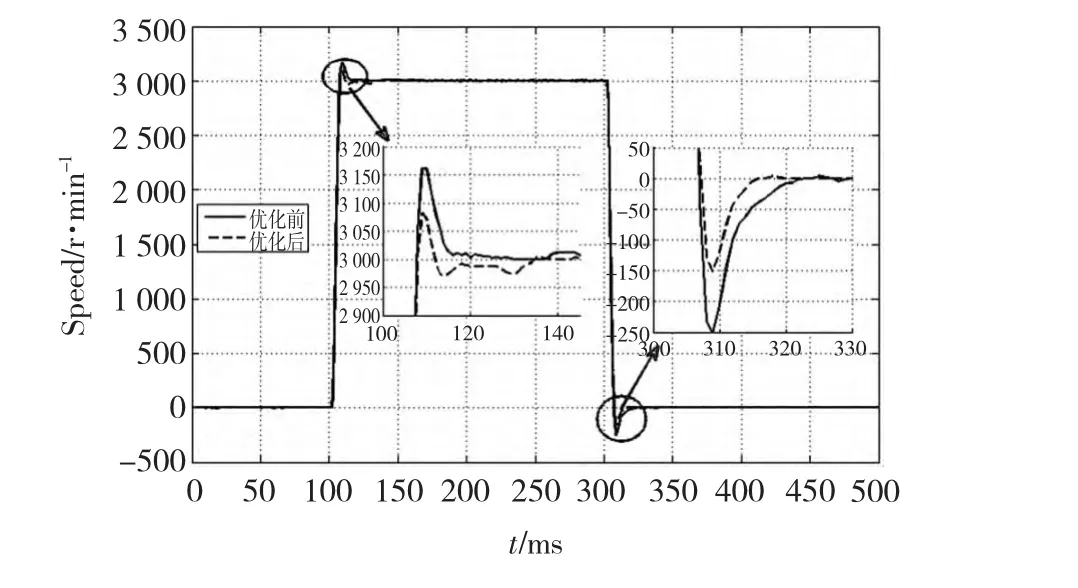
圖6 光軸時優化前后3 000 r/min階躍響應Fig.6 Speed step response with one times load inertia ratio

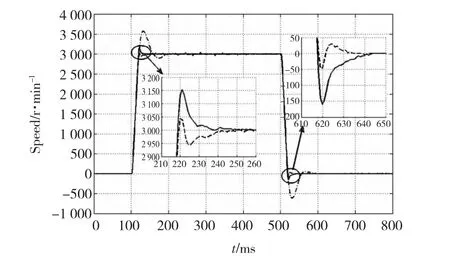
圖7 5倍負載慣量時3 000 r/min階躍響應Fig.7 Speed step response with 5 times load inertia ratio

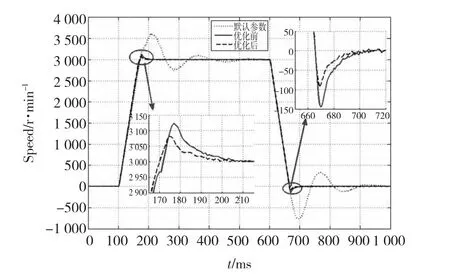
圖8 20倍負載慣量時3 000 r/min階躍響應Fig.8 Speed step response with 20 times load inertia ratio

一步整理出不同負載慣量下，系統默認參數、優化前后參數的伺服系統階躍性能指標如表1所示。

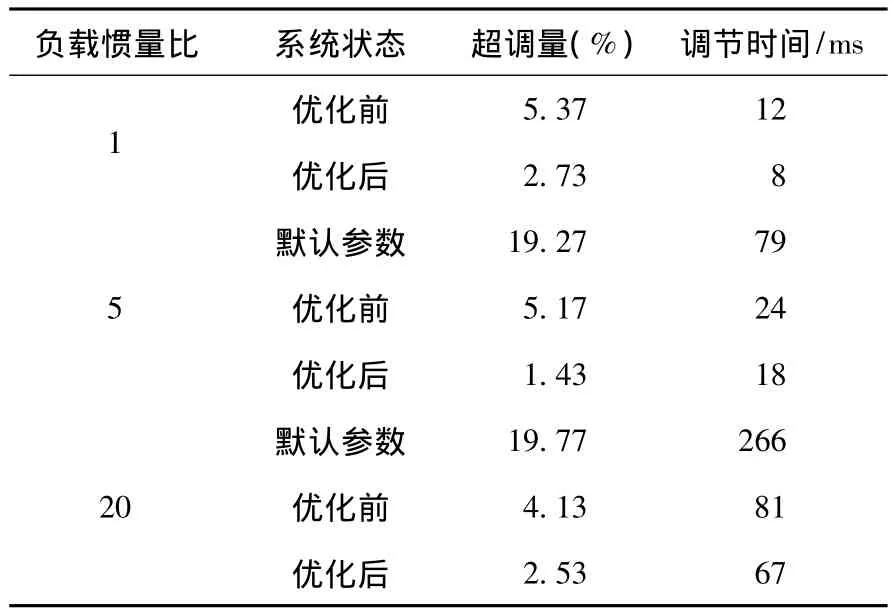
表1 不同負載慣量時伺服系統階躍性能指標Table 1 Performance index of speed step response with different times load inertia ratio

由表1數據可知，基于頻率法的理論參數已經能使伺服系統具有較好的響應性能;經過2DOF整定法優化后，伺服系統響應性能又有了大幅度提高:超調量明顯減小，調節時間明顯縮短。

圖9所示為在額定負載時，伺服系統在理論參數和迭代優化后參數下的3 000 r/min階躍響應和電流響應波形。圖10所示為加載測試平臺，加載系統(加載驅動器和電機)使用的是日系安川Σ5驅動器，整個加載測試平臺的慣量比為5。由圖9分析可知，在帶額定負載啟動時，采用2 DOF迭代優化后的參數比頻域法設計參數具有更好的系統動靜態性能。

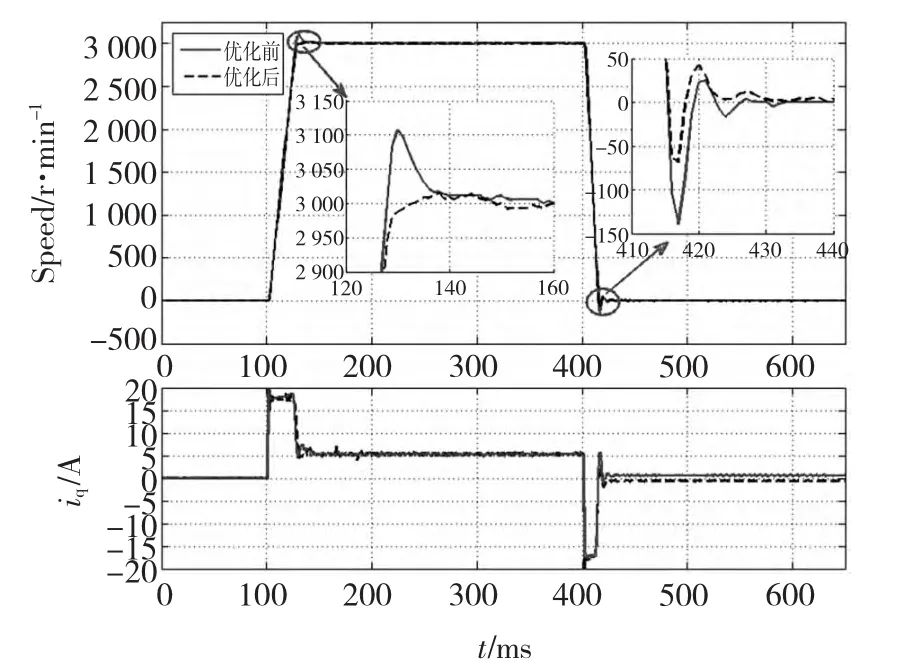
圖9 額定負載下系統3 000 r/min階躍響應Fig.9 Speed step response with rated load

圖10 加載測試平臺Fig.10 Loading test platform

圖11所示為伺服系統穩速3 000 r/min時突加突卸額定負載時的轉速波動。測試平臺仍采用圖10所示平臺。表2總結了在突加突卸額定負載時的系統轉速降落值，由表分析可知，采用2DOF迭代優化后的參數要比頻率法設計參數具有更好的抗負載擾動性。

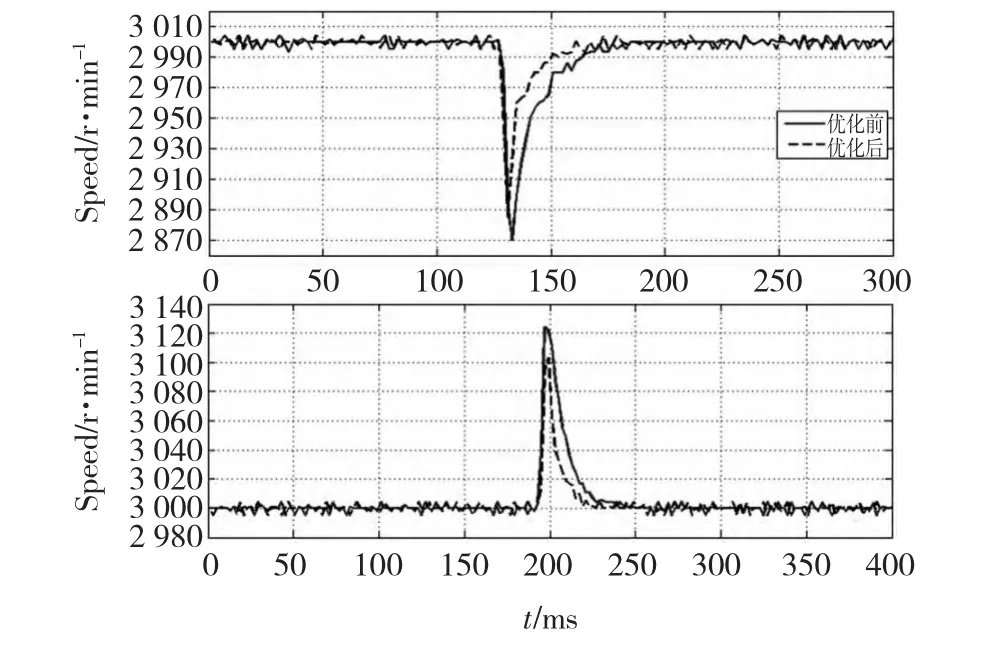
圖11 突加突卸額定負載時的轉速波動曲線Fig.11 Speed fluctuation when loading and unloading rated load

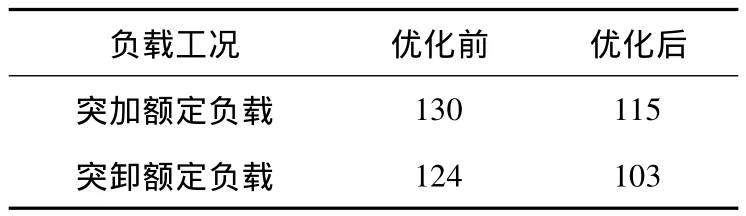
表2 突加突卸額定負載的轉速波動值Table 2 Speed fluctuation when loading and unloading rated loadr/min

4 結論

本文提出了一種新穎的PMSM伺服系統速度環參數自整定及優化方法，利用頻域法設計一組速度PI控制器參數，然后以該PI參數為初始值、ITAE為階躍響應的評價函數，通過2DOF整定法在初始值附近搜索使系統工作于最佳控制性能的PI參數值。該方法的特點在于通過頻域法設計的速度環PI參數已經使系統處于較佳控制性能，從而減少了2DOF的迭代步驟和時間。實驗結果證明，通過該方法整定得到的速度環PI參數能使伺服系統具有良好的動態跟蹤性能和較強的負載抗擾性。

［1］秦憶.現代交流伺服系統［M］.武漢:華中理工大學出版社，1995.

［2］CHEN Y Q，MOORE K L.Relay feedback tuning of robust PID Controllers with iso-damping property［J］.IEEE Transactions on Systems，Man and Cybernetics-Part B:Cybernetics，2005，35(1):23－31.

［3］ASTROM K J，HIGGLUND T.Automatic tuning of simple regulators with specifications on phase and amplitude margins［J］.Automatica，1984，20:645－651.

［4］TURSINI M，ZHANG D Q.Real-Time gain tuning of pi controllers for high-performance PMSM drives［J］.IEEE Transactions on Industry Applications，2002，38(4):1018－1019.

［5］WANG MingShyan，SHAU TzuChang，CHANG ChiaMing.DSP based auto tuning design of permanent magnet synchronous motor drives［C］//The 33rdAnnual Conference of the IEEE Industrial Electronics Society.Taiwan，2007:1044－1048.

［6］MUDI Rajani K，DEY Chanchal，LEE TsuTian.An improved aotu-tuning scheme for PI controllers［J］.ISA Transaction，2007，47(1):45－52.

［7］LIDOZZI A，SOLERO L，CRESCIMBINI F.Direct Tuning Strategy for Speed Controlled PMSM Drives［C］.IEEE International Symposium on Industrial Electronics，Italy 2008:1265－1270.

［8］陳鵬展，唐小奇，任清榮.基于IITAE評價指標的交流伺服系統參數自動整定研究［J］.微電機，2010，43(2):70－73.

CHEN Pengzhan，TANG Xiaoqi，REN Qingrong.Study on an parameters auto-tuning methods of AC servo system of IITAE evaluation indicators［J］.Micromotors，2010，43(2):70－73.

［9］楊明，張揚，曹何金生，等.交流伺服系統控制器參數自整定及優化［J］.電機與控制學報，2010，14(12):29－34.

YANG Ming，ZHANG Yang，CAO Hejinsheng，et al.Gain selftuning of PI controller and parameter optimum for PMSM drives［J］.Electric Machines and Control，2010，14(12):29－34.

［10］楊明，高揚，于泳，等.基于迭代學習控制的交流伺服系統PI參數自整定［J］.電機與控制學報，2005，9(6):588－592.

YANG Ming，GAO Yang，YU Yong，et al.On-line self-tuning of PI controller for PMSM drives based on the iterative learning control［J］.Electric Machines and Control，2005，9(6):588－592.