某型火箭炮多形態耦合發射動力學建模與仿真分析

馮 勇, 徐振欽

(南京工程學院 機械工程學院，南京 211167)

多管火箭發射系統是一個極其復雜的系統。火箭彈和發射架之間、系統各部分之間相互作用、相互制約，系統的剛度、阻尼和質量矩陣都隨時間不斷地改變。整個系統構成一個復雜的隨機非線性時變彈性系統，準確研究其發射過程中的動態特性將有助于設計的改進，避免樣機的重復制造，縮短研制時間和節省研制成本。

目前，發射動力學多采用多剛體系統動力學理論進行研究，近年來引入了柔性多體系統動力學理論[1-2]、剛液耦合多體動力學理論[3-4]等對發射動力學做了大量的多學科交叉研究工作，但全面考慮剛液/剛彈耦合效應的多管火箭炮發射動力學研究極為少見。本文以多剛體系統動力學和柔性多體系統動力學理論為基礎，考慮了剛液/剛彈耦合效應及地面支撐效應，建立了某型火箭炮的發射動力學模型并開展了相應的仿真研究，獲得了較為準確的結果，為工程研制、試驗提供了理論支持。

1 剛柔耦合多體動力學基本理論

研究剛柔耦合多體系統動力學問題，需將多剛體系統動力學和柔性多體系統動力學基本理論相結合。處理柔性多體動力基本學思路是，將柔性體離散化，以離散后若干個單元的有限個節點自由度去表示物體的無限多個自由度，單元的彈性變形可用少量模態的線性組合近似的表示。如果物體在坐標系的位置用它在慣性坐標系中的笛卡爾坐標X= (x，y，z) 和反映剛體方位的歐拉角Ψ=(ψ，θ，φ) 來表示，模態坐標用q= {q1，q2，…，qM} (M為模態坐標數) 來表示，則柔性體的廣義坐標可選為

(1)

柔性體的動能經計算可用廣義坐標表達式為：

(2)

式中，M(ξ)為柔性體的質量矩陣，其按移動坐標、轉動坐標和模態坐標可分為：

(3)

依據理論可知用拉格朗日乘子法建立第i個柔性體或剛體的動力學方程形式為

(4)

式中，T為柔性體或剛體的動能表達式；Qi為廣義力，包括單元彈性變形和外載荷引起的廣義力；λ為拉式乘子；nb為多體系統的構件個數，包括柔性體。

將方程(4)與系統約束方程C(ξ,t)=0聯立，即構成剛柔耦合多體系統動力學方程[5-6]。

2 全信息動力學模型的建立

2.1 某型火箭系統結構及其多體系統描述

多管火箭炮結構較為復雜，其結構如圖1所示，經合理簡化后建立其多體動力學模型，模型主要包含: 車體( 包括車大梁、板簧、鉸接件)、輪胎、底座、回轉支承、發射箱、定向器 、火箭彈等構件。

1.車體 2.發射箱 3.輪胎 4.回轉臺 5.支撐

對任意多體系統的拓撲構型表達方式而言，每個體記為Bi(i=1,…,N),N為系統中體的個數，鉸用一條連接鄰接剛體的有向線段表示，記為Hj(j=1,2,3…)，B0表示系統外運動為已知的剛體。本文所研究火箭系統的拓撲結構如圖2所示，其中：發射管的柔性效應直接影響火箭彈出管的運動參數變化，將對初始擾動產生不可忽略的影響，因此模型中將與體B19～B26相聯系的定向管建為柔性體；支撐B9、B10與地面B0間的鉸h9、h10及回轉臺B16與起落架B17間的鉸h24的功能主要通過液壓系統得以實現，因此應建立機械系統與液壓系統的耦合模型；車輪B1～B8與地面B0間的鉸h1～h8體現為輪胎與地面的彈性接觸效應，因此在模型中應建立真實反映這種彈性效應的輪胎-地面接觸模型。

圖2 某型火箭系統的拓撲結構

2.2 仿真模型的建立與參數確定

2.2.1 剛柔耦合模型的建立

為了簡化計算而又不失一般發射系統固有的動態特性，仿真模型的建立過程中，首先通過借助有限元分析工具，建立定向管的模態中性文件(MNF)，其中所設置定向管的材料特性為：密度7.8×103kg/m3，彈性模量206 GPa，泊松比0.3；然后將中性文件導入到多剛體模型中，通過Bushing彈性約束建立火箭彈與柔性定向管間的相互關系，從而構建出較為真實的剛柔耦合仿真模型[1]。

2.2.2 剛液耦合模型的建立

以往動力學建模中通常采用彈簧阻尼器來代替液壓系統的功能，往往存在很大的不合理性，不能很真實的反映液壓系統的作用以及該系統對火箭炮發射的影響。因此，在本文的動力學建模過程中引入液壓回路，以建立完全可以反映系統真實工作狀態的剛液耦合模型。通過剛液耦合動力學仿真可以方便地對液壓伺服系統、機械系統的參數進行反復聯調，以使液壓系統和機械系統達到最佳匹配。

運用Adams/View中的Hydraulic模塊能夠很好的模擬機械系統中液壓問題，并能夠與其它機構很好的兼容而最終完成剛液耦合問題。圖3所示為在Hydraulic模塊中建立的千斤頂支撐液壓閉鎖回路，該液壓回路主要由壓力源、方向控制閥、液壓鎖、油缸和單向閥組成，液壓系統中所用液壓元件型號的選定計算方法在此不再列出[4]。此外，高低機構的剛液耦合建模方法與千斤頂支撐機構的剛液耦合建模方法相同，在此不再贅述。

電液伺服閥是伺服回路中最重要的元件，它的性能決定了整個回路的性能。ADAMS/Hydraulics通過一個二階傳遞函數表示控制輸入信號i和滑閥位移x之間的關系：

(5)

式中，ω=2πf為伺服閥固有角頻率(rad/s)；f為對應于相位滯后90°的頻率(Hz)；ζ為阻尼系數。仿真分析中需要特別說明的是，由于沒有電信號的輸入，上述電液伺服閥的功能通過設置閥芯的位移函數來實現。

圖3 千斤頂支撐液壓回路

2.2.3 輪胎-地面接觸模型的建立

以往動力學建模中要么忽略輪胎地面的彈性接觸效應，要么采用彈簧阻尼器來模擬。但是，均不能很好的反映這種彈性接觸效應的影響。

在分析中，采用Fiala輪胎模型；不平路面由一系列三角形的平面單元組合成的一個三維表面，原理如圖4所示[5]，數字1、2、3等表示節點(Node)，這些節點的x、y坐標要滿足一定的規律，z坐標僅僅表示路面的寬度；這些節點按一定的規律組成路面單元(Element)。火箭炮發射時，底盤車懸架和輪胎均處于鎖死狀態，前輪著地以支承前端載荷，千斤頂支撐大部分后端載荷，后輪不離地支承部分載荷。輪胎和地面之間的載荷主要有輪胎變形和地面的摩擦力作用，因此只要在路面單元里設置合理的靜摩擦系數和動摩擦系數，就能模擬較為真實的火箭炮駐車發射過程中的輪胎路面彈性接觸效應(如圖5所示)[7]。此時，輪胎的受力情況為

(6)

式中，FZ、FY、FX分別為輪胎的法向、軸向和徑向受力；KZ為輪胎靜剛度；KY為輪胎側偏剛度；KX為輪胎剪切剛度；HZ為輪胎與地面的穿透值；HY為輪胎側偏變形量；HX為輪胎剪切變形量；CZ為輪胎阻尼系數；U0為靜摩擦力系數。

圖4 隨機不平路面原理圖

圖5 隨機不平路面原理圖

2.2.4 系統激勵分析

火箭在發射過程中，系統依次受到火箭發動機的推力、閉鎖擋彈機構的閉鎖力、火箭彈定向鈕與螺旋導槽的作用力、火箭彈與定向管間碰撞接觸力以及火箭彈燃氣射流對定向器的作用力。這些力是引起火箭炮彈架系統振動的主要激勵。

就本文所研究火箭炮而言，其火箭彈發動機的推力約為30 kN；閉鎖擋彈力約為18 kN；火箭彈定向鈕與螺旋導槽的作用力通過公式(6)來計算求得，平均側壓力約為約為12.9 kN；單個火箭彈與定向器間的碰撞接觸力如圖6所示；火箭彈燃氣射流對定向器的作用力是引起彈架系統產生強烈振動的主要原因，以定向器縱向軸線與炮口平面交點上的中心開始計算，作用在定向管上的載荷情況如圖7所示。

(7)

式中，RC為彈體回轉半徑；Rn為導轉鈕與螺旋槽接觸線中點的運動圓半徑；F為發動機平均推力；α為螺旋角。

圖6 火箭彈與定向器間的碰撞接觸力

圖7 沖擊力隨著火箭彈離炮口距離變化曲線

3 發射動力學仿真分析

3.1 仿真模型驗證

對仿真模型進行發射動力學仿真(高低射角16°；方向射角0°；發射間隔5 s)，計算參考坐標系為：以回轉臺的中心為原點，車體前進方向為x方向；垂直于x方向并向上的方向為y方向；z方向由右手法則確定。

圖8所示為三連發發射過程中發射架在高低平面內的角速度仿真變化曲線與定型樣炮的測試變化曲線對比圖，由結果對比來看，仿真變化曲線與測試變化曲線基本吻合。此外，表1給出了火箭炮系統固有頻率的仿真結果與實驗結果的對比，二者數據基本一致。以上的對比分析表明本文所采用的建模方法、仿真參數及液壓參數的選取是正確的，仿真所得到的結果是可信并可參考的。

表1 火箭炮固有振動頻率的比較

圖8 發射架在高低平面內的角速度仿真結果與測試結果對比

3.2 仿真結果分析

圖8、圖9所示為火箭彈發射過程中發射架在高低平面和回轉平面內的角速度變化曲線。由變化曲線可知，發射過程中發射架在回轉平面內的最大角速度約為0.035 rad/s，出現在第六枚火箭彈飛出定向管的瞬間；而在高低平面內的最大角速度約為回轉平面的兩倍左右為0.065 rad/s，出現在第一枚火箭彈飛出定向管的瞬間。以上結果分析發現，引起發射架在兩個平面內振動的主要激勵源不同，燃氣射流沖擊應當是引起發射架在高低平面內振動的主要原因，而火箭彈陸續發射后所引起發射箱重心位置的幾何偏置是引起發射架在回轉平面內振動的主要原因。

由圖8所示振動曲線來看，振動幅值較大且系統衰減周期(約為15 s)較長。這就意味著，當前一發彈引起的振動尚未結束時，后一發彈已經開始發射，繼而引起后續彈發射精度的下降。此外，從圖8、圖9所示曲線分析來看，發射架在高低平面和回轉平面內的振動頻率分別為1.3 Hz和1.4 Hz，與表1所示的火箭炮固有振動頻率測試值非常接近，極易引起系統的共振而導致發射精度的下降。為改變上述狀況，必須要選擇一個最佳的射擊周期。理論和實踐表明連發射擊的最佳射擊周期應為單發射擊炮口振動的顯著衰減周期(幅值從最高點衰減到最大幅值的20%所需時間)。由圖8所示的第三枚發射后的振動曲線分析來看，本系統等時隔連續發射擊的最佳射擊周期約為6 s左右。

圖9 發射架在回轉平面內的角速度

由圖9所示振動曲線來看，振動曲線呈現無規律、不順滑特征：在發射第一枚、第三枚及第七枚火箭彈時，發射架在回轉平面內的角速度幅值較小且衰減較快；而在發射第六枚火箭彈時，產生了整個發射過程中的最大幅值且衰減較慢。由此可見，該火箭炮的射序不盡理想，存在著進一步優化的可能。

圖10、圖11所示為火箭彈發射過程中發射架在高低平面和回轉平面內的動載變化曲線。由變化曲線可知，發射過程中發射架在高低平面內的最大動載荷約為420 kN，出現在第一枚火箭彈飛出定向管的瞬間，此后最大動載荷逐漸減小，通過分析可知，造成這種現象的主要原因在于：隨著火箭彈的發射，燃氣射流的迎風面積逐漸減小；而在回轉平面內的最大動載荷約為175 kN，也出現在第一枚火箭彈飛出定向管的瞬間，此后最大動載荷也逐漸減小，通過分析可知，造成這種現象的主要原因在于：隨著火箭彈的發射，發射箱中的載彈重量逐漸減小。

圖10 發射架在高低平面內的動載曲線

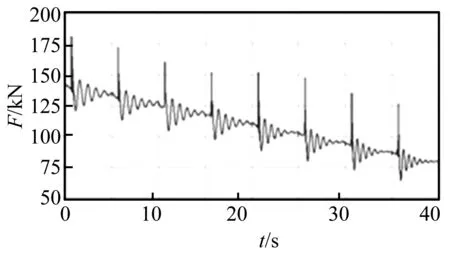
圖11 發射架在回轉平面內的動載曲線

此外，從圖10、圖11所示曲線來看，動載曲線光滑無跳躍，表明發射架在發射過程中運行平穩。由此可以說明，發射架與回轉平臺間的液壓回路的設計是合理的，液壓元件型號的選取也是合適的。

4 結 論

本文全面的建立了某型火箭炮的發射動力學模型并開展了相應的仿真研究，得到了一些有用的結論。

(1) 從全文的研究過程和最后的仿真結果可以表明，所采用地建立多態耦合的火箭炮發射動力學模型方法是可行的，利用該模型不僅可以全面細致地對系統開展力學特性研究還可以通過反復調整參數實現機械系統與液壓系統的最佳匹配。

(2) 火箭彈在發射過程中，燃氣射流沖擊力是引起發射架在高低平面內振動的主要原因，而火箭彈陸續發射后所引起發射箱重心位置的幾何偏置是引起發射架在回轉平面內振動的主要原因。

(3) 仿真結果表明，文中所建立的火箭炮系統模型采用等時隔連續射擊的最佳射擊周期約為6 s左右；表明火箭炮存在著進一步優化的可能。

(3) 發射過程中發射架在高低平面內和回轉平面內的最大動載荷分別為為420 kN和175 kN，均出現在第一枚火箭彈飛出定向管的瞬間。因此，在進行系統結構優化時應重點考察高低平面內動載荷的影響。

[1]馮勇, 馬大為, 薛暢, 等. 多管火箭炮剛柔耦合多體發射動力學仿真研究[J].兵工學報,2006,27(3):545-548.

FENG Yong, MA Da-wei, XUE Chang, et al. Simulation studies of coupled rigid and flexible multi-body dynamics for multiple launch rocket systems[J]. Journal of Acta Armamentari I, 2006,27(3):545-548.

[2]任杰，秦偉，馬大為，等. 某多管火箭炮車炮剛柔耦合極限路況行駛動力學研究[J]. 振動與沖擊,2011,30(3):199-204.

REN Jie，QIN Wei，MA Da-wei，et al. Driving dynamics of vehicle combined with rocket launcher under extreme conditions of road surface by applying the method of coupled rigid and flexible bodies[J]. Journal of vibration and shock, 2011,30(3):199-204.

[3]徐振欽,樂貴高,馬大為. 機液耦合多管火箭發射系統動力學仿真[J]. 彈箭與制導學報,2005,25(4):179-181.

XU Zhen-qin,LE Gui-gao, MA Da-wei. Simulation of launch dynamics coupled with mechanism-liquid model for multiple launch rocket system[J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2005,25(4):179-181.

[4]馮勇,馬大為,宋曉峰,等.某箱式火箭炮電液伺服系統交互式仿真研究[J].兵工學報,2006,27(2),363-366.

FENG Yong, MA Da-wei, SONG Xiao-feng,et al.Interactive simulation of electronic and hydraulic servo system about clustered canister rocket launching platform[J]. Journal of Acta Armamentari I, 2006,27(2):363-366.

[5]洪嘉振. 多體系統動力學-理論、計算方法和應用[M]. 上海 :上海交通大學出版社, 1992 .

[6]劉延柱,洪嘉振,楊海興. 多剛體系統動力學[M]. 北京 : 高等教育出版社, 1980.

[7]馮勇，徐振欽. 基于發射動力學仿真的某履帶戰車改優研究[J].系統仿真學報,2009,21(15),4896-4899.

FENG Yong, XU Zhen-qin. Improvement study of track chariot basing on launch dynamics simulation[J]. Journal of System Simulation, 2009,21(15):4896-4899.