氣流偏角對不同形狀復合材料壁板熱顫振特性的影響

高 揚，楊智春，谷迎松

(西北工業大學 航空學院，西安 710072)

壁板顫振是高超音速飛行器壁板結構在空氣動力、慣性力和彈性力的相互耦合作用下產生的一種氣動彈性不穩定現象，是一種自激振動。影響壁板顫振的因素有很多，比如材料、邊界條件、幾何尺寸和氣流偏角等，國內在這些方面已經開展了一系列研究。苑凱華等[1]建立了考慮熱效應的復合材料壁板顫振的非線性有限元模型，計算了壁板的顫振臨界速壓并分析了其非線性顫振特性。葉獻輝等[2]用迦遼金方法建立了三維壁板熱環境下顫振方程，分析討論了兩種溫度分布和幾何尺寸對系統穩定性的影響。周秀芳等[3]研究了超音速氣流中二維壁板的熱顫振，將wash out 濾波器技術與Normal Form直接法相結合，設計了控制器的線性、非線性增益，有效地降低了顫振極限環的幅值。楊超等[4]建立了氣動熱、氣動彈性雙向耦合高超音速二維曲面壁板顫振分析方法。楊智春等[5-6]建立了考慮熱效應的復合材料壁板顫振分析模型，給出了頻域和時域的顫振方程求解方法，結果表明在超音速的壁板顫振分析中必須考慮熱效應的影響，且壁板形狀也是影響顫振邊界的一個重要因素，并提出了一種分步求解的方法進行了復合材料壁板的熱顫振分析，結果指出鋪層方式是影響壁板顫振臨界速度的一個重要的可設計因素。

然而，目前研究的壁板顫振問題都是針對矩形壁板的，對于其他形狀壁板還鮮有研究。相同面積下采用其他形狀壁板是否會帶來更好的顫振特性還是一個未知的問題，因此研究其他形狀壁板的顫振特性對高超音速飛行器的防顫振設計有重要意義。對于飛行器來說，由于偏航角的存在，氣流方向并不總是沿飛行器軸線方向，因此氣流偏角也是影響壁板顫振特性的重要因素。上世紀六十年代末和七十年代初，氣流偏角對超音速氣流中各向同性材料和正交各向異性材料矩形板顫振臨界速壓的影響得到了研究。Korders等[7]和Bohon[8]研究了任意氣流偏角對簡支邊界條件下各向同性材料和正交各向異性材料矩形板顫振特性的影響。Durvasula[9-10]應用瑞利-李茲法分別研究了簡支邊界和固支邊界下氣流偏角對矩形各向同性材料壁板顫振臨界速壓的影響。Kariappa等[11]和Sander等[12]應用有限元方法(FEM)研究了氣流偏角對于各向同性材料平行四邊形壁板顫振的影響。Shyprykevich等[13]和Sawyer[14]從理論和實驗方面研究了顫振臨界速壓對氣流偏角和柔性支持邊界的依賴性。Cheng等[15]用有限元方法研究了氣流偏角和熱載荷共同作用下矩形壁板的穩定性邊界問題。王曉慶等[16]建立了考慮氣流偏角的壁板熱顫振方程，進行了不同氣流偏角下的壁板熱顫振分析及多目標優化設計。同矩形壁板一樣，氣流偏角對不同形狀壁板顫振特性也會產生影響，因此，本文在進行不同形狀復合材料壁板的顫振特性研究時同時考察了氣流偏角和熱載荷的影響。

本文首先建立了同時考慮氣流偏角和熱載荷影響的層合復合材料壁板顫振分析的有限元模型，應用分步求解復合材料壁板熱顫振速度的方法，針對面積相同而形狀不同的壁板進行了顫振分析，考察了氣流偏角對不同形狀壁板熱顫振特性的影響。

1 考慮氣流偏角的復合材料壁板熱顫振有限元模型

在壁板的熱顫振分析中通常采用三個簡化假設：①壁板結構的變形不影響溫度場；②顫振響應的時間尺度遠小于溫度變化的時間尺度，因此在壁板的熱顫振分析中可以將溫度場看作是穩態的；③在溫升不太高的情況下忽略溫度對材料特性的影響。

考慮復合材料層合壁板的熱顫振問題，由von Karman非線性應變位移關系，壁板總應變為中面位移產生的應變、考慮大變形時撓度引起的面內附加應變和彎曲產生的應變的和：

(1)

橫向剪切應變為

(2)

其中，u0，v0，w0為中面位移，θx和θy為中面分別繞x軸和y軸的轉角。

令ε0=εm+εmb，則層數為NL的復合材料層合板的內力表達式可寫為：

(3)

其中

(4)

假設氣流平行于壁板表面，流速為V，氣流方向與x軸的夾角為Λ，考慮氣流偏角的一階活塞理論的氣動力表達式[15]為

pa=p∞-p=

(5)

根據虛功原理可以得到考慮氣流偏角的復合材料壁板熱顫振有限元方程：

(6)

式中mb為質量矩陣,ca，ka分別為氣動阻尼矩陣和氣動剛度矩陣，kb，km，kbm，αsks組成了小變形下的彈性剛度矩陣,kNm為面內位移在板彎曲自由度上產生的附加剛度，kΔT為熱應變產生的附加剛度，PmΔT，PbΔT為溫度場引起的載荷。

對于具有對稱鋪層的復合材料壁板，有kbm=0，當溫升沿板的厚度方向均勻分布時，有PbΔT=0。

因而，式(6)可以寫成解耦的形式

(7)

式(7)是由一個靜力學方程和一個動力學方程組成的。本文采用一種分步求解的方法[5]，即先求解壁板面內的結點位移wm，進而獲得面內附加剛度kNm和熱附加剛度kΔT，第二步將第一步求解得到的熱效應剛度kNm-kΔT帶入動力學方程中，就能夠對定常溫度場下壁板的顫振特性進行分析。

2 考慮氣流偏角的復合材料壁板熱顫振分析

為了驗證本文考慮氣流偏角熱顫振分析方法的有效性，針對文獻[14]中給出的壁板熱顫振分析算例，求解其顫振邊界，并與其結果進行對比。算例中矩形復合材料壁板的幾何尺寸為38.1×30.5×0.122cm，邊界條件為四邊固支，氣流偏角分別為Λ=0°,15°,30°,45°。

為了直接與參考文獻[14]的結果進行對比，對壁板溫升進行了無量綱化處理，即以壁板的絕對溫升值ΔT與壁板屈曲溫升ΔTcr的比ΔT/ΔTcr來度量壁板的溫升。同時對壁板的顫振速壓進行無量綱化處理，無量綱速壓定義為：

(8)

式中q=ρv2/2，D110是復合材料的鋪層角度全部為零時彎曲剛度的第一項。

求解出該壁板無量綱顫振臨界速壓隨無量綱溫升的變化關系與文獻[14]的結果對比如圖1所示。

圖1 本文結果與參考文獻[14]的對比

由圖1可見，本文計算所得無量綱顫振臨界速壓隨無量綱溫升的變化趨勢與參考文獻[14]完全一致，且誤差在3%以下，可見本文分析方法對壁板屈曲溫度以下考慮氣流偏角的熱顫振分析有著較高的準確性。

3 氣流偏角對不同形狀壁板熱顫振特性的影響

本節研究如圖2所示具有相同面積的矩形壁板、梯形壁板和三角形壁板的熱顫振特性。壁板厚度均為0.762 mm，鋪層方式為[0/45-45/90]s，由石墨/環氧材料制成，材料主方向沿x軸正方向，材料的性能參數見表1。邊界約束方式為周邊固支。氣流方向與x軸正方向夾角為氣流偏角，逆時針為正。

表1 石墨/環氧材料的力學性能參數表

圖2 面積相等的矩形壁板、梯形壁板和三角形壁板

圖3 不同形狀壁板顫振臨界速壓隨溫升變化

圖4 不同形狀壁板顫振臨界速壓隨氣流偏角變化

不同溫升下三種不同形狀壁板的顫振臨界速壓隨氣流偏角Λ的變化情況如圖4所示。

(3)在氣流偏角Λ=0°～180°的變化范圍內，相同溫升下，三角形壁板的顫振臨界速壓高于梯形壁板，梯形壁板高于矩形壁板。

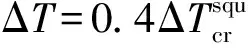
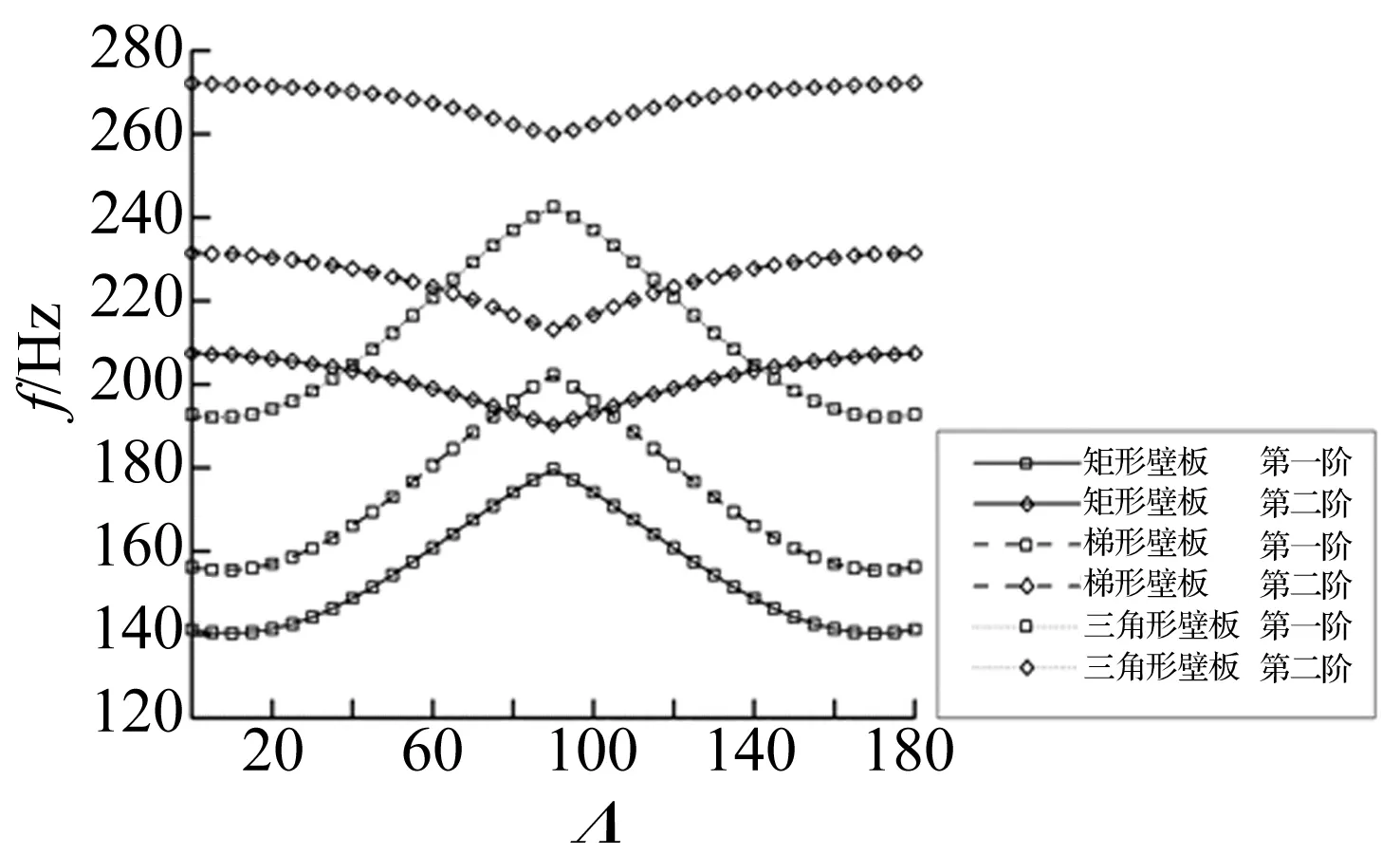
圖5 不同形狀壁板氣動彈性模態頻率隨氣流偏角變化規律

由圖5可見，三塊不同形狀壁板第一階氣動彈性模態的頻率在氣流偏角Λ=0°～90°和Λ=90°～180°的變化范圍內隨著氣流偏角的增大先減小再增大，在氣流偏角為Λ=5°～10°時和Λ=170°～175°時分別達到最小值，在氣流偏角為Λ=90°時達到最大值。第二階氣動彈性模態的頻率隨著氣流偏角的增大先減小后增大，當氣流偏角為Λ=90°時達到最小值。由圖可見，三塊不同形狀壁板的前兩階氣動彈性模態的頻率差在氣流偏角為Λ=0°～90°和Λ=90°～180°的變化范圍內隨著氣流偏角的增大先減小再增大，在氣流偏角為Λ=5°～10°時和Λ=170°～175°時分別達到最大值，在氣流偏角為Λ=90°時達到最小值。由于三塊不同形狀壁板的顫振都是由其第一階和第二階氣動彈性模態發生耦合而產生的，根據顫振頻率重合理論，發生耦合的這兩階模態的頻率越接近，顫振越容易發生。由此可以解釋在圖4中Λ=5°～10°時和Λ=170°～175°時三塊壁板的顫振速度達到極大值的原因。

4 結 論

本文建立了同時考慮氣流偏角和熱載荷影響的顫振分析有限元模型，通過對三塊面積相同形狀不同的復合材料壁板進行顫振分析，得到了三塊復合材料壁板的顫振臨界速壓隨氣流偏角和溫升變化的曲線，研究表明：

(1)氣流偏角為零時，不同形狀壁板的顫振臨界速壓隨溫升的升高而近似呈線性下降；在不同溫升時三角形壁板的顫振臨界速壓高于梯形壁板，梯形壁板高于矩形壁板，且溫升對三角形壁板顫振速壓的影響最大，對梯形壁板的影響最小。

(2)在氣流偏角Λ=0°～90°和Λ=90°～180°的變化范圍內，矩形壁板、梯形壁板和三角形壁板的顫振臨界速壓都呈現出先增大后減小的規律，且在氣流偏角為Λ=5°～10°和Λ=170°～175°時都分別達到最大值，在氣流偏角為Λ=90°時達到最小值。

(3)在所考察的氣流偏角情況下，三角形壁板的顫振臨界速壓高于梯形壁板，梯形壁板高于矩形壁板。

對于面積相同形狀不同的復合材料壁板，熱載荷和氣流偏角對顫振邊界的影響不同。熱載荷降低了壁板的顫振臨界速壓，不同的氣流偏角對壁板有不同的影響，若結合壁板形狀的可設計性進行顫振優化設計，則可有效提高壁板的顫振臨界速壓，改善復合材料壁板的熱顫振特性。

[1]苑凱華,邱志平.高超音速氣流中復合材料壁板熱顫振分析[J].南京航空航天大學學報,2010,42(3):313-317.

YUAN Kai-hua, QIU Zhi-ping. Flutter analysis of composite panels in hypersonic flow with thermal effects [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010,42(3):313-317.

[2]葉獻輝，楊翊仁.三維壁板熱顫振分析[J].振動與沖擊，2008，27(6)：55-59.

YE Xian-hui, YANG Yi-ren. Thermal flutter analysis of a three-dimension panel [J].Journal of Vibration and Shock, 2008，27(6)：55-59.

[3]周秀芳，曹樹謙. 用Normal Form直接法研究壁板的熱顫振與控制[J].振動與沖擊，2012，31(11):54-56.

ZHAO Xiu-fang, CAO Shu-qian. Thermal flutter and control of a panel using normal form direct method[J].Journal of Vibration and Shock,2012,31(11):54-56.

[4]楊超，李國曙，萬志強.氣動熱-氣動彈性雙向耦合的高超聲速曲面壁板顫振分析方法[J].中國科學，2012,42(4)：369-377.

YANG Chao, LI Guo-shu, WAN Zhi-qiang. Aerothermal-aeroelastic two-way coupling method for hypersonic curved panel flutter [J]. Scientia Slnica Technologica,2012,42(4):369-377.

[5]楊智春，夏巍，孫浩.高速飛行器壁板顫振的分析模型和分析方法[J].應用力學學報，2006,23(4)：537-542.

YANG Zhi-chun, XIA Wei, SUN Hao. Model and analysis of panel flutter of high speed vehicle [J]. Chinese Journal of Applied Mechanics, 2006,23(4):537-542.

[6]楊智春，譚光輝，夏巍.鋪層方式對復合材料壁板熱顫振特性的影響[J]. 宇航學報，2008,29(3):1047-1052.

YANG Zhi-chun,TAN Guang-hui, XIA Wei. Effects of stacking sequence on thermal flutter speed of composite panel [J]. Journal of Astronautics,2008, 29(3):1047-1052.

[7]Korders E E and Noll R B. Theoretical flutter analysis of flat rectangular panels in uniform coplanar with arbitrary direction[R]. NASA TN D-1156, Edwards California: NASA Flight Research Center, 1962.

[8]Bohon H L. Flutter of flat rectangular orthotropic panels with biaxial loading and arbitrary flow direction[R]. NASA TN D-1949, Hampton Virginia: NASA Langley Research Center, 1963.

[9]Durvasula S. Flutter of simply supported, parallelogrammic, flat panels in supersonic flow [J].AIAA Journal, 1967, 5(9): 1668-1673.

[10]Durvasula S. Flutter of clamped skew panels in supersonic flow [J]. Journal of Aircraft, 1971, 8(6):461-466.

[11]Kariappa V, Somashekar B R, Shah C G. Discrete element approach to flutter of skew panels with In-plane forces under yawed supersonic flow[J]. AIAA Journal, 1970, 8(11): 2017-2022.

[12]Sander G, Bon C, Geradin M. Finite element analysis of supersonic panel flutter [J]. International Journal for Numerical Methods in Engineering, 1973, 7(3): 379-394.

[13]Shyprykevich P, Sawyer J W. Orthotropic panel flutter at arbitrary yaw angles-experiment and correlation with theory [C]. AIAA, 11th Aerospace Sciences Meeting, Washington DC, 1973:192-202.

[14]Sawyer J W. Flutter of elastically supported orthotropic panels including the effects of flow angle[R]. NASA TN D-7491, Hampton Virginia: NASA Langley Research Center, 1974.

[15]Cheng G F, Mei C, Lee Y Y. Flow Angle, Temperature and aerodynamic damping on supersonic panel flutter stability boundary[J].Journal of Aircraft, 2003, 40(2): 248-255.

[16]王曉慶,韓景龍,張軍紅.不同氣流偏角下的壁板熱顫振分析及多目標優化設計[J].航空學報，2010，31(11):2195-2201.

WANG Xiao-qing, HAN Jing-long, ZHANG Jun-hong. Thermal flutter analysis of panel and multi-objective optimization design considering variations of flow yaw angle[J]. Acta Aeronautica et Astronautica Sinica11，2010，31(11):2195-2201.

[17]Ashley H, Zartarian G. Piston theory-a new aerodynamic tool for the aeroelastician [J], Journal of Aeronautical Science, 1956, 23(10): 1109-1118.