大型液壓離心振動臺的耦合特性分析

羅中寶，楊志東，叢大成，張 兵

(哈爾濱工業大學 機電工程學院，哈爾濱 150001)

為了研究地震環境下的土動力學特性、地基液化、邊坡穩定性、泥土-地基-結構間的耦合關系，發達國家相繼建成了一系列大型離心振動臺，這些離心振動設備在其本國土工領域發揮著舉足輕重的作用[1]。鑒于中國嚴峻的地震形勢和土工領域研究的迫切需求，中國地震局工程力學研究所聯合哈爾濱工業大學，正在研制國內第一大、世界第二大單軸離心振動臺[2]。

土工巖土材料，其動態特性都具有很強的非線性，這些特性與巖土應力、巖土應力歷史密切相關。離心機可以提供一個離心加速度場來補償物理原型的自重應力。通過對巖土自重應力的補償，可利用小比尺物理模型來精確模擬實際工程原型在地震激勵下的響應。與此同時，離心振動試驗也提供了解釋巖土變形、結構失效等問題的試驗數據，這些數據可以為巖土動力學模型的推導及修正提供依據。因此，離心振動臺被認為是當今世界土工抗震領域最先進、最有效的試驗設備之一。

世界上已建成的土工離心振動臺約有25臺，國外最具代表性的研究機構包括美國加州大學戴維斯分校、美國科羅拉多大學和美國倫斯勒工學院；國內最具代表性的研究機構包括南京水利科學研究院、清華大學和香港科技大學[3]。相比而言，國內振動臺在振動負載、振動加速度、振動頻寬等方面，與國外先進水平有較大差距。而國外的振動臺研制時間較早，現階段的工作重心已從振動臺的研制轉移到土工離心實驗上來，所以國內外關于大型離心振動臺研制的可用資料相對較少。總的來說，離心振動臺相比普通振動臺而言，受以下兩方面因素的影響：① 受離心機裝機容量的限制，振動臺基礎的質量和剛度有限；② 受離心振動復合環境的影響，振動臺中液壓元件的動態特性發生改變。鑒于上述影響因素，在離心振動臺的研制過程中需著重解決以下三方面問題：① 輕柔基礎、液壓執行機構、巖土模型的耦合特性分析；② 離心振動復合環境對液壓元件的影響，特別是對三級電液伺服閥動態特性的影響；③ 離心振動臺控制策略的研究。針對以上三方面問題，國內外學者已進行一些研究。

目前，三級伺服閥在離心力振動復合環境下的特性分析研究，幾乎處于空白。但前人關于兩級伺服閥在離心力環境下的特性分析經驗值得借鑒。賀云波根據伯努利方程和流體沖量定理，分析了兩級電液伺服閥在離心工作環境下的輸入電流與閥芯位移間的關系。文中指出當伺服閥順臂安裝時，離心加速度與伺服閥的零偏電流近似成正比[4]。董云雷也對該問題也進行了深入研究，并分析了離心力場下的油液傳輸特性，提出了離心液壓的概念[5]。

由于離心振動實驗的持續時間非常短，一般采用三狀態控制的伺服控制策略來提高位置閉環系統的頻寬，采用離線迭代的振動控制方法來校正振動臺的驅動信號。Ketcham等[6]提出了這種對驅動信號的校正算法，用以提高離心振動滑臺對高頻加速度信號的復現能力。Mason等[7]闡述了UCD-CGM實驗中心最近一系列土工離心實驗中所使用參考信號的選擇方法及對應的過濾過程。Mason也采用離線迭代頻響函數的方法來校正驅動信號，實驗表明該方法可使振動臺輸出信號與參考信號近似達到一致。

相比問題②、③而言，輕柔基礎、執行機構、巖土模型的耦合特性是研究②、③問題的基礎，是現階段離心振動臺研究最需解決的問題。Fiegel等[8-9]定性評價了小比尺模型、模型箱和振動臺之間的耦合關系。Ketcham[10]在研制科羅拉多的離心振動滑臺時，也發現了在滑臺運動時，吊籃響應具有低、高頻共振的特點。此后，Ilankatharan[11]定量分析了離心振動臺中液壓執行機構、巖土模型和輕柔基礎間的動態耦合，并采用Opensees工具對該耦合關系進行仿真。但是，前人研究都沒能準確建立起輕柔基礎、執行機構、巖土模型的耦合數學模型。本文將集中解決該問題，詳細推導并分析輕柔地基、執行機構、巖土模型的耦合關系。

1 離心振動系統簡介

圖1是香港科技大學離心振動系統(HKUST)的結構示意圖。如圖所示，離心振動系統大致可分為以下6部分：① 吊籃及振動臺系統；② 轉臂；③ 平衡配重；④ 驅動電機；⑤ 變速箱；⑥ 離心機主軸。驅動電機帶動離心機主軸旋轉，主軸的旋轉速度受變速箱調控；離心機主軸經轉臂支撐帶動轉臂旋轉，使振動臺上的巖土模型處于離心力場中，達到補償物理原型自重應力的目的。振動臺系統隨吊籃一起做離心運動，可以不停機地連續觸發多次地震波。

如圖2所示，圖中為哈工大與中國地震局工程力學研究所聯合研制的單軸離心振動臺，其離心機的裝機容量為300 gt，最大離心加速度為100 g，最大振動負載1 500 kg，最大振幅12 mm，最大水平加速度為30 g，最大振動頻率為350 Hz。該離心振動臺包括以下6部分：① 吊籃；② 伺服閥及液壓缸；③ 上平臺；④ 剪切軸承；⑤ 支撐板；⑥ 蓄能器。各部分的詳細情況如下。

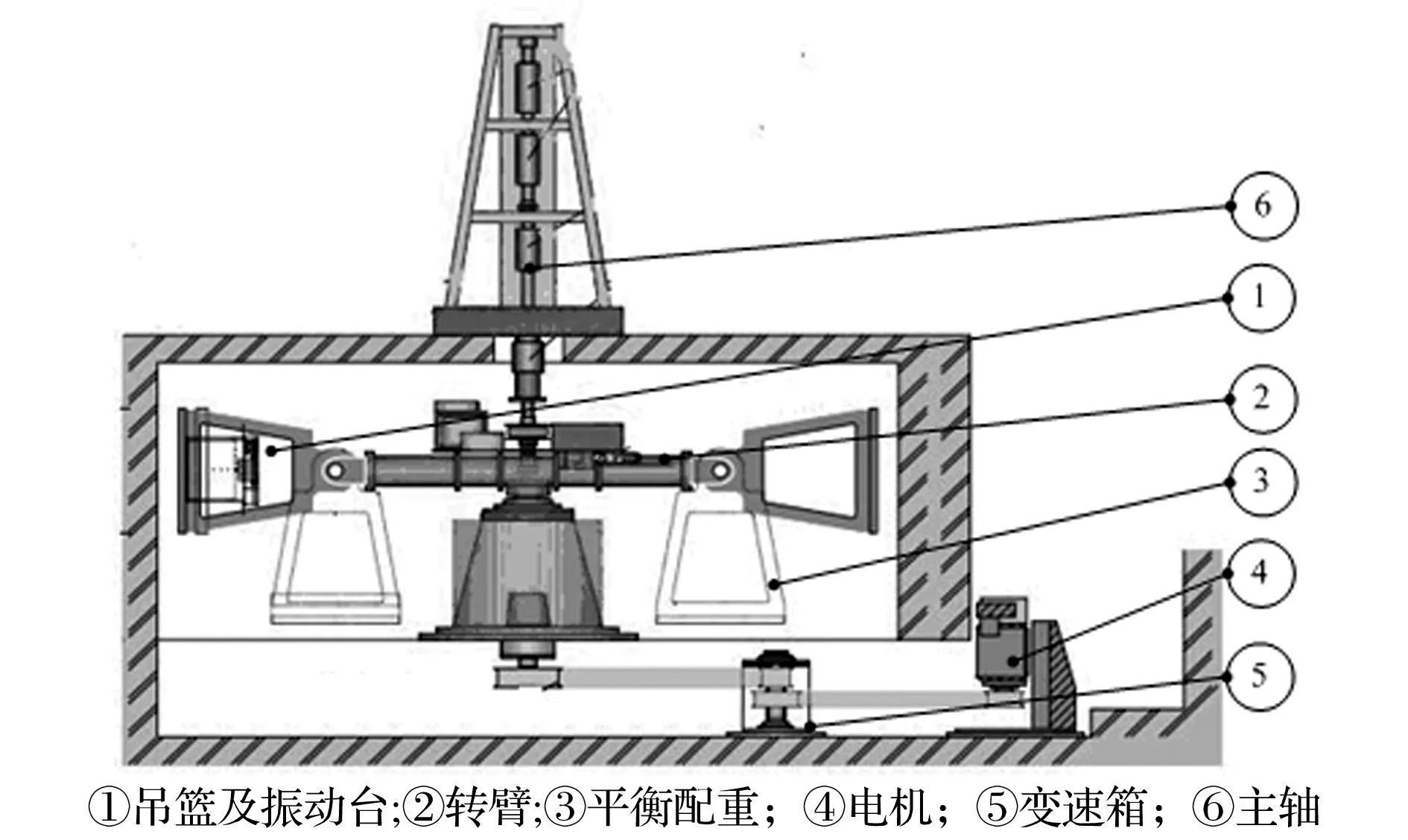
圖1 離心振動系統示意圖

圖2 哈工大、中國地震工程力學研究所聯合研制的離心振動臺

① 吊籃：吊籃的材質為Q345，包括2個吊耳和1個底座；吊籃通過2個吊耳與離心機臂相連，底座的內部做成柵格狀，以減少底座重量。

② 支撐板：支撐板固定在吊籃上，用以安裝蓄能器、液壓缸、伺服閥和剪切軸承；在支撐板內部鉆有油孔，用以整個液壓系統的供油和回油。

③ 蓄能器：離心振動臺配備了4臺蓄能器，作為短時間激振的油源使用；這種供油方式相比通過地面油源供油而言，減少了離心力對液壓系統的影響。

④ 剪切軸承：支撐板與上平臺間安裝了28個橡膠剪切軸承，用來支撐上平臺、巖土模型的離心負載。

⑤ 液壓缸與伺服閥：離心振動臺所采用的伺服閥是哈爾濱工業大學自行研制的大型三級伺服閥，液壓缸采用兩條非對稱液壓缸做一條對稱液壓缸使用，原理圖如圖3所示。另外，液壓缸與上平臺之間添加凹形運動塊，允許上平臺繞幾何中心做小幅轉動。

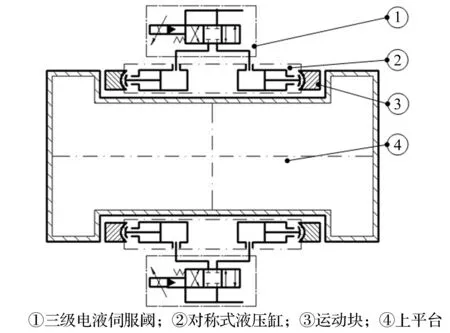
圖3 離心振動臺中使用的液壓缸和伺服閥

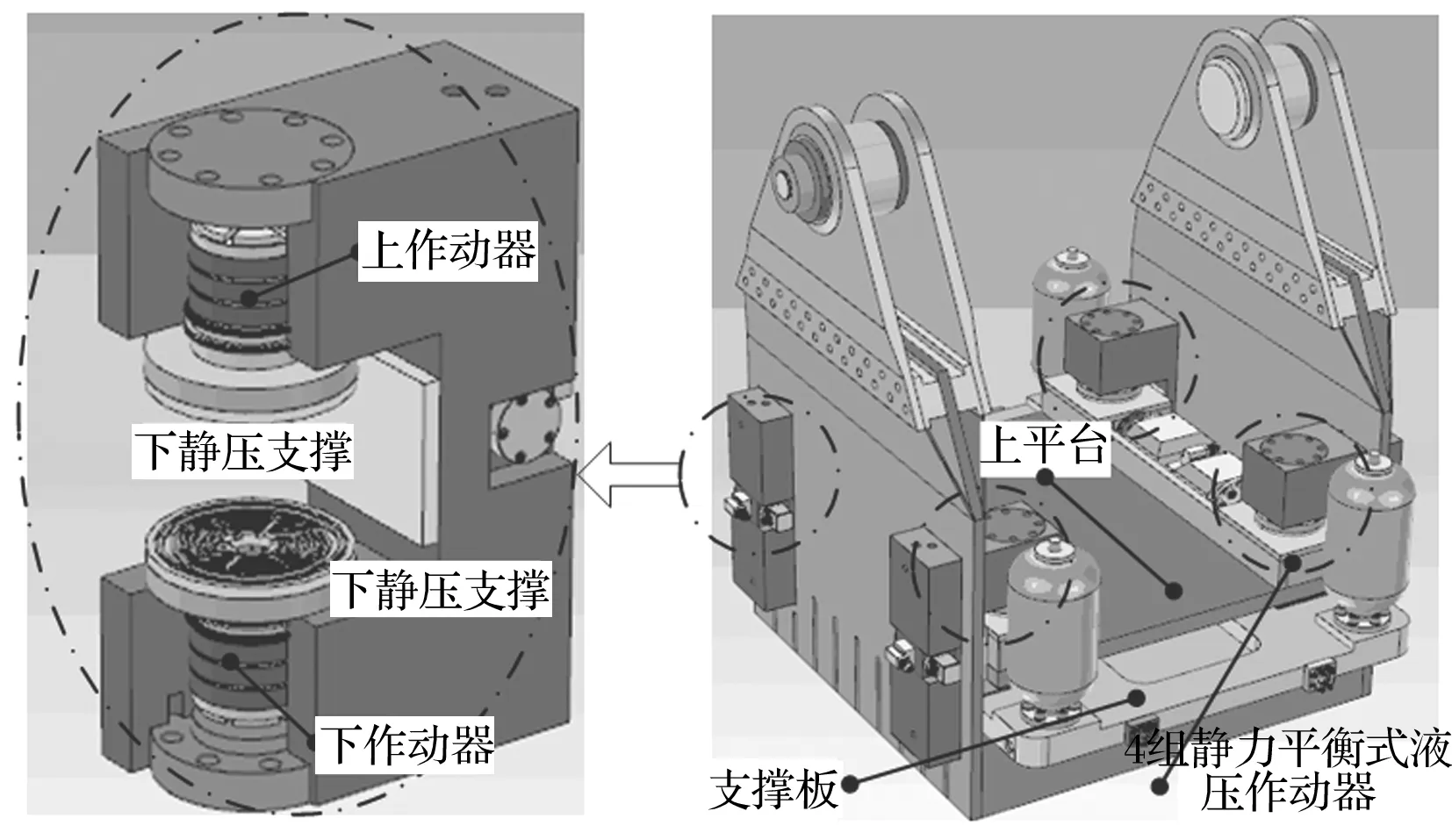
圖4 離心振動臺中使用的靜力平衡式液壓作動器

除此之外，由于剪切軸承在大位移運動時的水平向彈性力非常大，嚴重影響了離心振動臺波形復現的精度。哈爾濱工業大學正在研制靜力平衡式液壓作動器來代替橡膠剪切軸承，其三維實體模型如圖4所示。文中的靜力平衡式液壓作動器由一組不完全平衡型靜壓支撐和一組液壓作動器構成。通過控制作動器的出力差，達到抵消離心力的目的。由于不完全平衡型靜壓支撐的摩擦系數僅為0.002 5～0.003，因此該支撐方式還可大大減小上平臺運動過程中的摩擦力。對于一個靜壓支撐而言，上平臺與靜壓支撐緊密配合，作動器出力的90%由支撐中的高壓油膜支撐，10%由支撐的密封圈承受。總的來說，通過在離心振動臺中引入靜力平衡式液壓作動器可抵消離心力，并減小水平激振過程中的摩擦力。此外，該支撐方式也可以作為垂向激振使用，為單軸離心振動臺向水平、垂直雙向離心振動臺的改造提供條件。

2 輕柔基礎動態特性的等效

為了理論推導的方便，將輕柔基礎簡化為連續質量彈簧；由于離心振動臺中包含兩套執行機構，每套執行機構所對應輕柔基礎的質量為整個吊籃質量的一半，上平臺質量也為振動臺臺面質量的一半。如圖5所示，液壓缸缸筒固定在輕柔基礎上，缸筒隨輕柔基礎的變形而產生位移。連續質量彈簧在液壓缸反力(F1,F2)的作用下，會產生與上平臺振動方向相反的加速度，并發生一定量的彈性變形。為了便于系統傳遞函數的推導，希望將輕柔基礎的動態特性等效成圖5中所示的一維質量-彈簧-阻尼系統。在等效過程中需遵循以下三點原則：① 等效質量-彈簧-阻尼系統的固有頻率與連續質量彈簧的一階固有頻率保持一致；② 等效質量-彈簧-阻尼系統中輕柔基礎的加速度方向與上平臺的振動方向相反，加速度大小與基礎質量成反比；③ 激振頻率保持一致，對于圖2中的離心振動臺而言，動態激振力主要為剪切軸承變形引起的彈性力。在下面的內容中，將詳細敘述該等效模型的推導過程。

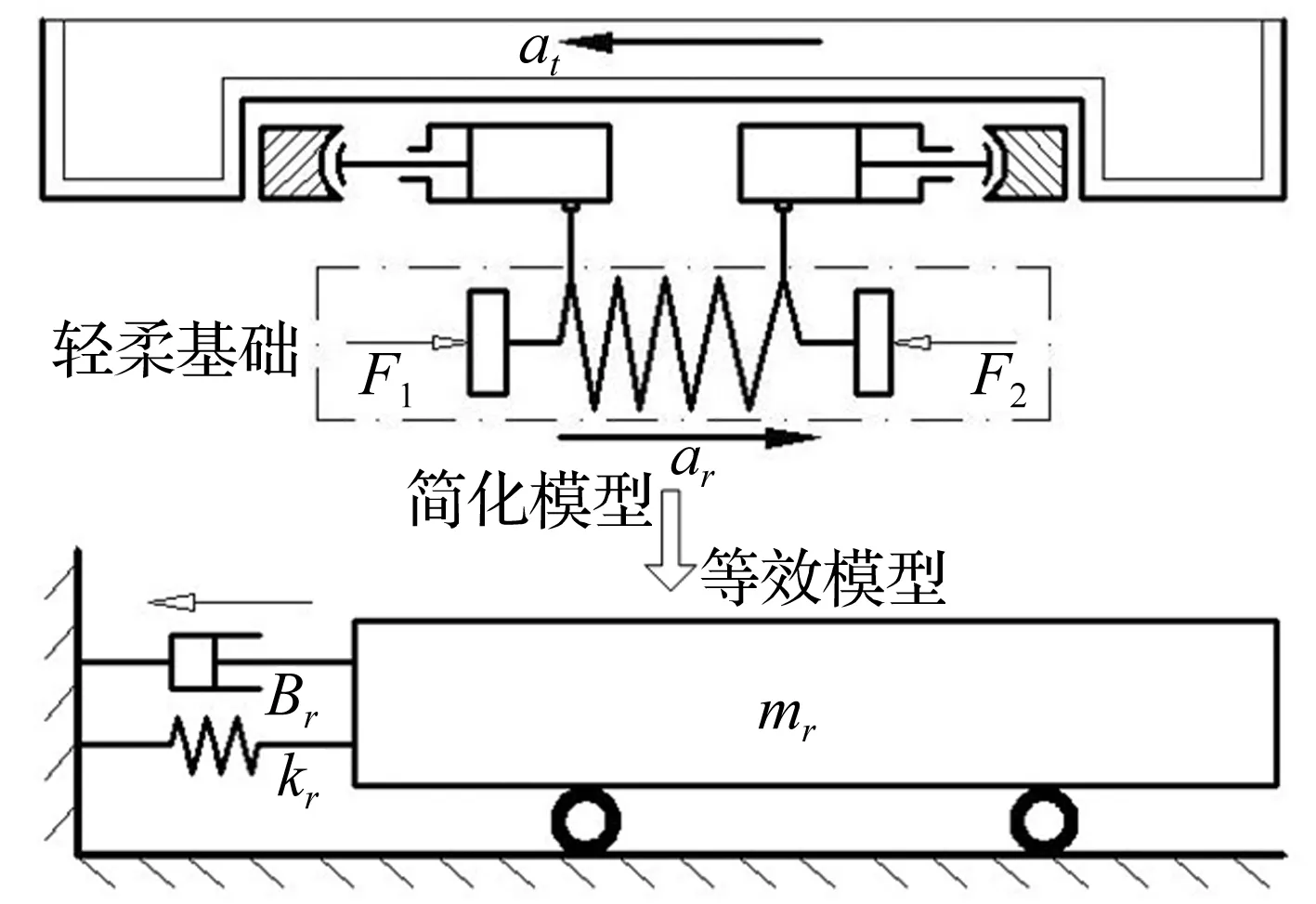
圖5 輕柔基礎與液壓執行機構的耦合關系

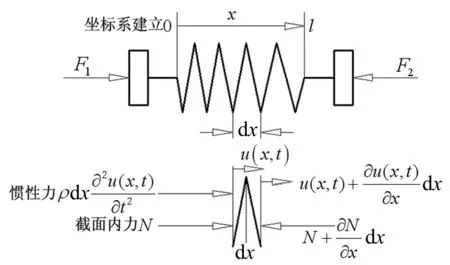
圖6 連續質量彈簧的受力分析

僅考慮連續質量彈簧在水平方向上的變形，建立如圖6所示的坐標系。任取一小微元作為研究對象，根據達朗貝爾原理可得(令F1>F2)：

(1)

式中，ρ表示連續質量彈簧的線密度；u(x,t)表示位置x處質點的運動；N表示彈簧截面處的內力。

化簡上式可得：

(2)

其中，截面內力N可根據胡克定律進行計算：

(3)

式中，k表示連續質量彈簧的整體剛度；l表示彈簧的長度。

因此，將式(3)代入式(2)，可得連續質量彈簧的運動控制方程：

(4)

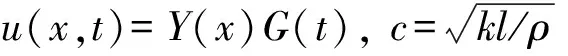
(5)

令等式兩邊都等于-(ω/c)2，可得：

(6)

上述常微分方程的通解可以表示為：

G=Csinωt+Dcosωt

A,B,C,D由邊界條件和初始條件所確定。文中的連續質量彈簧，滿足以下三個邊界條件。

(1) 左端點的力邊界條件

(2) 右端點的力邊界條件

(Csinωt+Dcosωt)

又因為F1+F2=PsAp，其中Ps表示油源壓力，Ap表示活塞的有效作用面積。因此可得：

然后上式兩端分別對時間求導數：

(7)

(3) 中間點的力邊界條件

同樣，等式兩邊同時對時間求倒數，可得：

(8)

聯立式(7)、式(8)便可求得系統的固有頻率。觀察式(7)、式(8)，在B=0的情況下，系統的固有頻率可表示為：

i=0,1,2,…

(9)

如前所述，系統的激振力主要是剪切軸承變形引起的彈性力。由于離心振動臺中安裝了28個剪切軸承，振動時每個剪切軸承的變形量也不同，因此很難準確估算系統各個激振力的大小，但各激振力的頻率是可近似估算的。眾所周知，彈性力與上平臺、輕柔基礎間的相對位移成正比，液壓缸出力卻與上平臺的絕對加速度成正比。據此，剪切軸承變形引起的彈性力的頻率與液壓缸出力的頻率近似相同。因此，在等效模型中使用液壓缸出力作為激振力，來模擬輕柔基礎在外載荷激勵下的響應。表面上看來，如此等效激振力并不是非常精確，但從本質上來說這種等效方式卻準確模擬了輕柔基礎共振時的極限情況。當液壓缸出力的頻率與輕柔基礎任一固有頻率重合時，在彈性力的作用下，輕柔基礎發生共振，輕柔基礎上任一點的位移都近似無窮大，此時激振力的大小并不重要，激振力的頻率起主導作用。因此，相比準確等效激振力的大小而言，準確模擬激振力的頻率顯得更為重要。

3 耦合傳遞函數的推導

(1) 滑閥的流量方程

假設：滑閥為理想零開口四通滑閥，四個節流窗口是匹配、對稱的；節流窗口處的流動是紊流，流體壓縮性在閥內予以忽略；油源壓力恒定不變，回油壓力近似為0。此時，滑閥的流量方程可表示為式(10)：

qL=kqxv-kcpL

(10)

式中，qL表示滑閥的負載流量；kq表示滑閥的流量增益；xv滑閥的閥芯位移；kc滑閥的流量-壓力系數；pL負載壓降。

(2) 流量連續性方程

假設：液壓缸每個工作腔內各處壓力相同，油液溫度和體積彈性模量認為是常數；液壓缸的內、外泄漏為層流流動。此時，流量連續性方程表示為式(11)：

(11)

式中，Ap表示液壓缸活塞的有效作用面積；xt表示上平臺的絕對位移；xr表示輕柔基礎的絕對位移；ctp表示總泄漏系數；Vt表示總壓縮體積；βe表示油液的體積彈性模量。

(3) 力平衡方程

假設：忽略模型箱的動態特性，忽略巖土模型與模型箱間的摩擦力；上平臺與剪切軸承之間的摩擦力也忽略不計。 此時，分別以輕柔基礎、上平臺和巖土模型的整體、上平臺為研究對象，根據牛頓第二定律，建立式(12～14)的力平衡方程。

脈巖多呈北西向及北東向產出，主要類型有細粒花崗巖脈、花崗斑巖脈、閃長玢巖脈、安山玢巖脈、英安玢巖脈等。

首先，以輕柔基礎為研究對象，進行受力分析，可得式(12)：

(12)

式中，mr表示輕柔基礎的質量(包括缸筒質量)；xr表示輕柔基礎的位移；Br表示等效模型的阻尼；kr表示等效模型的剛度。

然后，以上平臺和巖土模型的整體為研究對象，進行受力分析，可得式(13)：

(13)

式中，mt表示上平臺的質量；ms表示巖土模型的質量；xs表示巖土模型在上平臺上的相對位移。

最后，單獨以上平臺為研究對象，進行受力分析可得，可得式(14)：

(14)

式中，Bs表示巖土模型的阻尼；ks表示巖土模型的剛度。

(4) 幾何補充方程

實際系統中，位移傳感器的兩端分別固定在缸筒和上平臺上，其測量的是輕柔基礎與上平臺之間的相對位移，因此位移傳感器的輸出位移y滿足式(15)中的幾何關系：

y=xt+xr

(15)

將式(10)～式(15)進行拉普拉斯變換，利用其變換結果便可得到考慮輕柔基礎、液壓執行機構、巖土模型耦合特性的系統傳遞函數，其方框圖如圖8所示。為了便于公式的推導，定義如下變量：

總的流量-壓力系數：kce=kc+ctp；

經詳細推導，位移傳感器輸出y與閥芯位移xv間的傳遞函數，最終可表示為如式(16)所示：

(16)

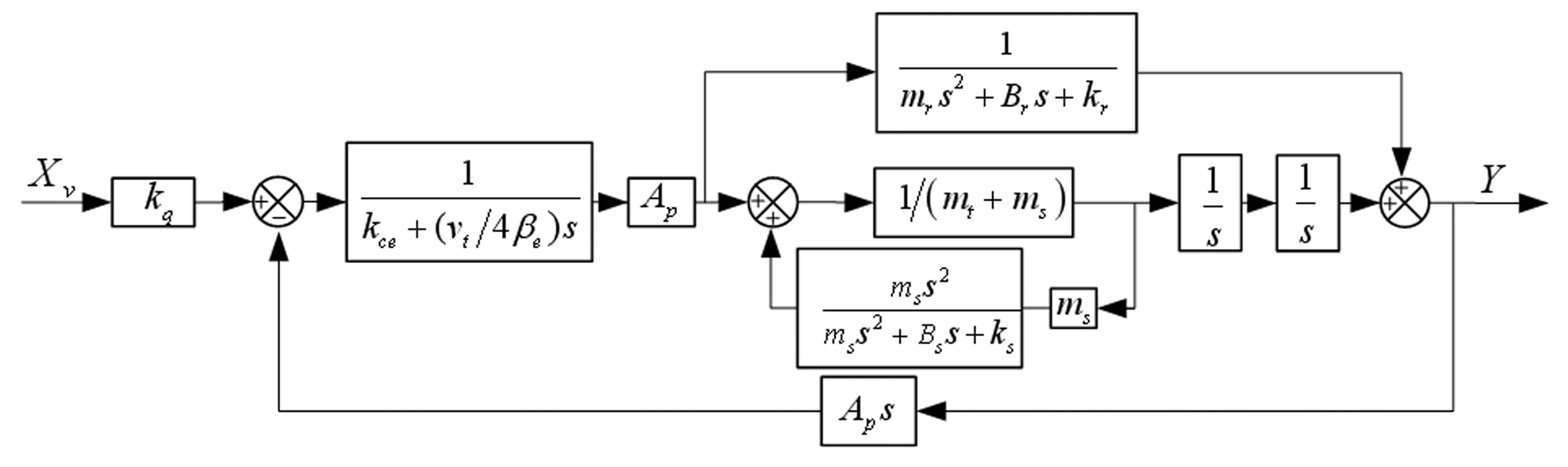
圖8 耦合系統的傳遞函數

式中ωrts、ξrts、ωrts′、ξrts′由方程組式(17)確定。根據式(16)和式(17)，當滿足mr遠大于(mt+ms)、kr→∞的邊界條件時，W(s)=W′(s)，系統的傳遞函數可簡化為僅有慣性負載時理想對稱閥控制對稱缸的傳函形式。

(17)

4 耦合傳遞函數的仿真分析

根據文中第二部分輕柔基礎動態特性的等效方法，求取了等效一維質量-彈簧-阻尼系統的固有頻率、阻尼比。再結合實際離心振動臺中液壓執行機構的實際參數，對系統的耦合特性進行仿真，仿真參數如表1所示，所有仿真參數已經過一定圓整。

在不考慮伺服閥動態特性的情況下，伺服閥輸入電壓與閥芯位移xv成正比，位移傳感器輸出y與伺服閥輸入電壓之間的傳遞函數如圖9所示。如圖9，系統的幅頻、相頻特性都具有明顯的波峰波谷。如曲線1所示，在低頻段(10～100 Hz)，耦合系統的幅頻特性近似按照-20 dB/dec下降，與理想積分環節類似。原因如下：如式(16)所示，耦合系統包括7個極點、4個零點。低頻段的兩對零、極點，距離非常接近，具體來說，極點-17.7±296i與零點-13.6±304i距離很近；極點-9.64±622i與零點-9.63±623i幾乎可以完全抵消。因此，在低頻段，耦合系統特性與理想積分環節類似；另外，在高頻段(100～1 000 Hz)，耦合系統的諧振頻率為363 Hz，遠大于不考慮耦合特性的液壓固有頻率(187 Hz)。另外，比較曲線1和曲線2可得：當巖土模型的固有頻率發生改變時，曲線2在(45～100 Hz)范圍內，幅頻特性變化劇烈，不能近似等效為積分環節。這也從側面說明巖土模型動態特性對耦合系統特性有較大影響。在實際的地基液化實驗中，巖土模型的剛度(或固有頻率)在實驗過程中逐漸降低，耦合系統的動態特性也隨之發生改變。

表1 耦合系統的仿真參數

在不考慮伺服閥動態特性的情況下，上平臺絕對位移xt與閥輸入電壓間的傳遞函數如圖10所示。相比于不考慮耦合關系時液壓執行機構的傳遞函數，考慮耦合關系的傳遞函數的幅頻、相頻特性具有明顯的波峰波谷。如圖10所示，幅頻特性在50 Hz和100 Hz處，幅度突然增大，這說明傳遞函數分子包含兩個固有頻率分別為50 Hz和100 Hz的二階微分環節，相比圖9中曲線1的傳遞函數而言，上平臺絕對位移xt與閥輸入電壓間的傳遞函數中又引入了一組不可對消的零極點。

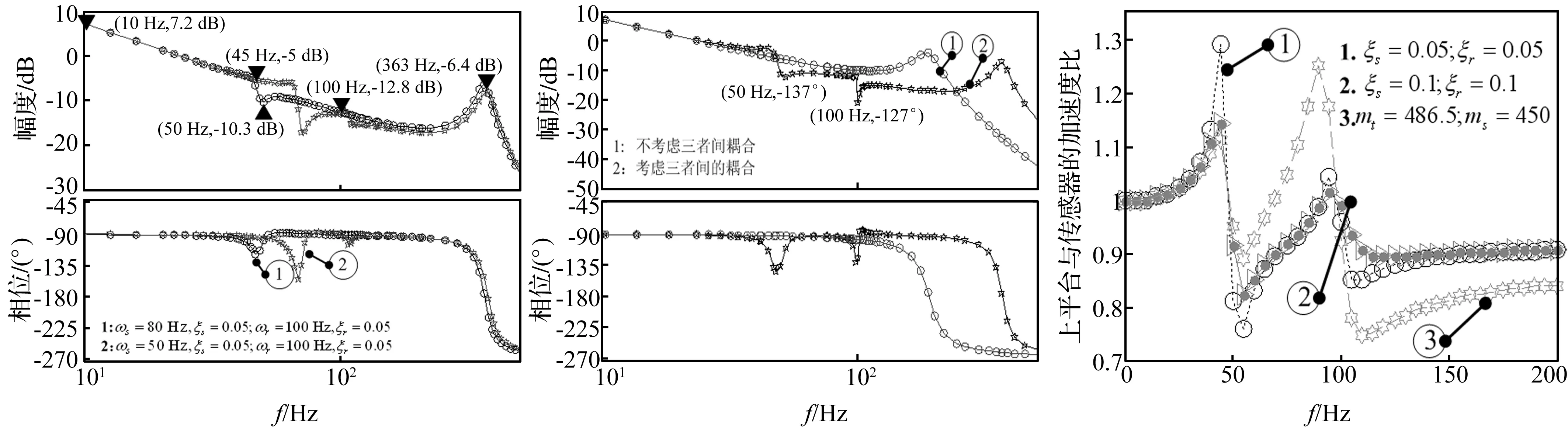
圖9 耦合系統的傳遞函數

離心振動臺是通過位移傳感器進行位置閉環，而實際控制量是上平臺的絕對加速度，因此需要研究上平臺絕對加速度與位移傳感器二階微分之間的關系。為敘述的方便，將位移傳感器輸出的二階微分定義為傳感器的加速度。如圖11所示，上平臺、傳感器的加速度比與頻率密切相關，上平臺加速度at(s)與傳感器加速度a(s)間的傳遞函數可表示為式(18)所示：

(18)

由傳遞函數可得，在ωs、ωr頻率附近，二者加速度比達到極小值，此結論在圖11中也得到了驗證。文中從能量角度來解釋該現象：從能量的角度來講，在巖土模型和輕柔基礎的固有頻率附近，巖土模型和輕柔基礎發生共振，其運動占據了系統的大部分能量，此時上平臺的所占能量相對較少，因此此時加速度比到達極小值。同理，在耦合固有頻率ωrts、ωrts′處，二者加速度比達到最大值，此時上平臺達到共振，其運動占據了系統大部分能量。與此同時，從圖11中還可以看出：巖土模型、輕柔基礎的阻尼比對二者加速度比的影響較大，阻尼比越小二者加速度比變化越激烈；另外，在150 Hz以上的高頻段，二者加速度比趨于恒定值。當mt=286.5 kg、ms=650 kg時，二者加速度比值為0.918；當mt=486.5 kg、ms=450 kg時，二者加速度比值為0.868。該結論可以通過式(18)來進行驗證，當ω→∞時，二者之間的比值與上平臺的質量成反比，上平臺的質量越大，二者加速度比值越小。為了在上平臺上精確復現加速度信號，應該盡量減小上平臺的質量，使上平臺加速度與傳感器加速度更加接近。此時，通過傳感器的位置閉環，便可以使上平臺的加速度滿足要求。

5 離心振動臺伺服控制策略的研究

如圖12所示，離心振動臺的伺服控制策略主要包括以下四部分：① 自由度分解與自由度合成；② 前置濾波器；③ 三狀態反饋；④ 順饋控制器。下面將對上述四部分的作用及設計原則作簡要說明，詳細信息見文獻[12]。

(1) 自由度分解、合成矩陣。自由度分解矩陣是將自由度位置偏差信號轉換為兩個單系統的偏差信號，驅動相應的激振器運動。自由度合成矩陣是將兩個單系統的反饋信號(位置、速度和加速度信號)轉化為自由度反饋信號。對于圖2中的離心振動臺而言，包括以下兩個自由度：① 沿水平方向上的平動；② 沿上平臺中心的轉動。在振動臺工作時，僅希望振動臺沿水平方向平動，不允許平臺繞中心轉動，繞中心轉動自由度的參考信號始終為0。離心振動臺的自由度分解Hf、合成矩陣Hh可表示式(19)所示。

(19)

(2) 前置濾波器。前置濾波器分為兩部分：① 利用高通濾波器對低頻加速度信號進行濾波；② 利用積分環節將加速度信號轉換為位置信號。本文前置濾波器的轉折頻率設定為10 Hz，其傳遞函數如下式所示：

(20)

式中ar、xr分別表示振動臺的加速度、位置參考，ω0=62.8 rad/s、ξ0=0.5。

(3) 三狀態反饋。三狀態反饋控制器引入加速度反饋來提高系統的阻尼比，通過對阻尼比的補償，可以進一步提高系統增益，從而達到提高系統頻寬的目的。引入速度反饋也可以提高系統頻寬，但速度反饋會降低系統的阻尼比。文中離心振動臺的三狀態反饋參數如下：加速度反饋系數ka=0.002 7，速度反饋系數kv=0.05，位移反饋增益kv=0.666 7，閉環前置增益ku=7.6。加入三狀態反饋前后，傳感器加速度與參考加速度間的傳遞函數如圖13所示。加入三狀態反饋以后，系統液壓固有頻率處的阻尼比顯著增大，諧振峰幅值顯著減少。另外，系統的頻寬也從45 Hz左右提升至液壓固有頻率附近(190 Hz)。

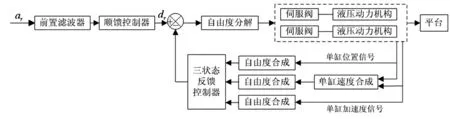
圖12 伺服控制策略的原理簡圖

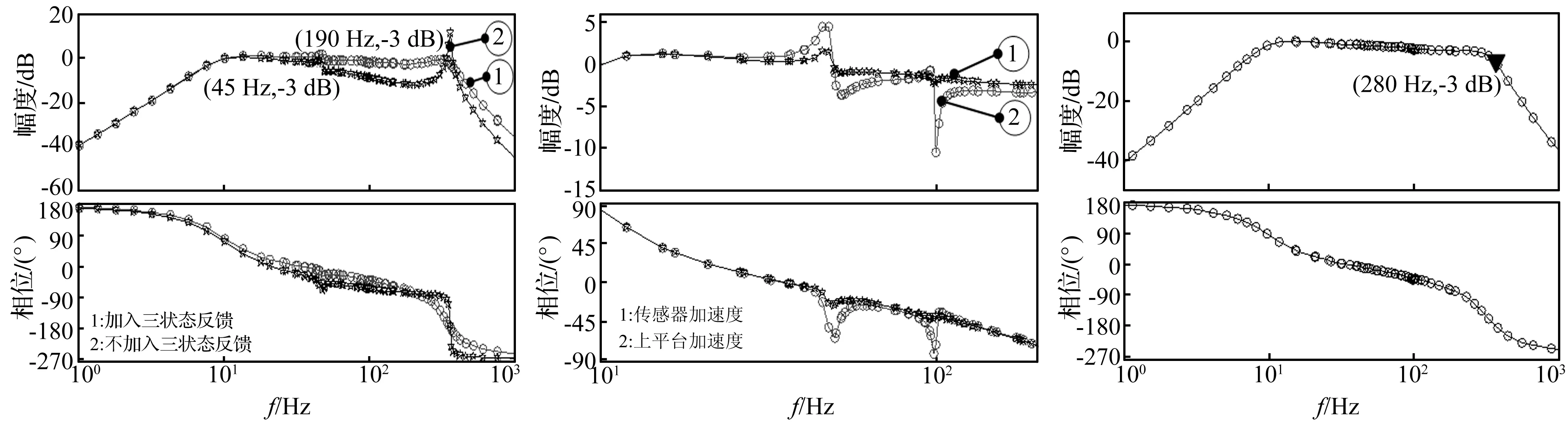
圖13 三狀態反饋對系統性能的影響

(4) 順饋控制器。順饋控制器的目的是對消閉環系統的主導極點，達到提高系統頻寬的目的。在離心振動臺中，控制目標是上平臺的加速度，而不是位移傳感器的加速度，上平臺、傳感器加速度在10～200 Hz范圍內的對比圖如圖14所示。從圖14中可以看出，由于零極點沒有完全對消，嚴重影響了系統的頻寬。通過辨識系統閉環傳遞函數，設計順饋控制器來對消頻寬范圍內的零極點，順饋控制器GFF如式(21)所示。

(21)

經過前饋控制器對消零極點后，上平臺加速度與參考加速度間的傳遞函數如圖15所示。如圖15所示，系統的頻寬提高到10～280 Hz。

6 結 論

文中研究了離心振動臺中輕柔基礎、液壓執行機構、巖土模型的耦合關系，完成了以下三方面的工作：① 將輕柔基礎簡化為連續質量彈簧，推導了輕柔基礎固有頻率的估計方法，并給出了輕柔基礎動態響應的等效方法；② 推導輕柔基礎、液壓執行機構、巖土模型的耦合數學模型，給出了位移傳感器輸出與伺服閥閥芯位移間的傳遞函數；③ 研究了離心振動臺的伺服控制策略，通過前置濾波器、三狀態反饋、順饋控制器的設計，可使離心振動臺復現頻寬范圍內的高頻加速度參考信號。

雖然文中已經得到一些有用的結論，但是離心振動臺中還存在諸多亟待解決的問題：

(1) 離心振動復合環境對液壓元件的影響。本文在研究輕柔基礎、液壓動力機構、巖土模型的耦合關系時，沒有考慮離心振動復合環境對液壓元件的影響。由于振動臺振動方向與離心力方向垂直，因此離心力在液壓缸上產生附加負載較小，應主要考慮離心力對三級電液伺服閥的影響。文中將電液伺服閥簡化為一個比例環節，與實際情況不符。因此，下階段應重點研究在離心振動復合環境下三級電液伺服閥垂臂安裝時的動態特性。

(2) 輕柔基礎固有頻率的估計。文中為了理論推導的方便，將輕柔基礎等效為連續質量彈簧。但實際輕柔基礎為減少質量，做成了柵格狀，很難通過理論推導得到輕柔基礎的固有頻率。從文中的推導也可以看出，輕柔基礎的動態對系統性能有較大影響。因此，希望在后續研究中，能夠引入實驗模態分析的方法來辨識輕柔基礎的固有頻率。

(3) 順饋控制器的設計。文中順饋控制器的設計依賴于對系統閉環傳遞函數零極點的準確辨識。在實際情況中，離心振動臺系統由于巖土模型的變形、蓄能器壓力降低等原因，本身就是一個非線性時變系統，因此很難完全通過順饋控制抵消掉頻寬內的零極點。在實際的研制過程中，還需引入魯棒控制策略來保證在一定系統參數變化范圍內，系統能夠穩定并達到一定性能。

[1]張建民, 于玉貞, 濮家騮, 等. 電液伺服控制離心機振動臺系統研制[J]. 巖土工程學報, 2004, 26(6): 843-845.

ZHANG Jian-min, YU Yu-zhen, PU Jia-liu, et al. Development of a shaking table in electro-hydraulic servo-control centrifuge[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 843-845.

[2]王永志. 振動離心機系統工作原理與初步設計[D]. 哈爾濱: 中國地震局工程力學研究所, 2010.

[3]Wilson D W, Boulanger R W, Feng X, et al. The NEES geotechnical centrifuge at UC DAVIS[C]// 13th World Conference on Earthquake Engineering. Vancouver:Prentice-Hall, 2004.

[4]He Y B, Chua P S K, Lim G H. Performance analysis of a two-stage electrohydraulic servovalve in centrifugal force field[J]. Journal of Fluids Engineering, 2003, 125(1): 166-170.

[5]董龍雷. 離心力-振動復合力學環境的模擬與控制[D]. 西安: 西安交通大學, 2004.

[6]Ketcham, Ko H Y, Sture S. Performance of an earthquake motion simulator for a small geotechnical centrifuge[C]// Centrifuge 91. Rotterdam:Balkema, 1991.

[7]Mason H B, Kutter B L, Bray J D, et al. Earthquake motion selection and calibration for use in geotechnical centrifuge[C]// ICPMG 2010. Rotterdam:Balkema, 2010.

[8]Fiegel G L, Idriss I M, et al. Effect of model containers on dynamic soil response[C]// Centrifuge 94. Rotterdam:Balkema, 1994.

[9]Narayanan. Modeling the seismic response of stratified soil (Graduate Dissertation)[D]. Davis: UC Davis, 1999.

[10]Ketcham. Development of an earthquake motion simulator for centrifuge testing and the dynamic response of a model sand embankment(Doctoral Dissertation)[D]. Boulder: University of Colorado, 1989.

[11]Ilankatharan M. Centrifuge modeling for soil-pile-bridge system with numerical simulations accounting for soil-container-shaker interaction(Doctoral Dissertation)[D]. Davis: UC Davis, 2008.

[12]馬軍輝. 吊籃剛度對離心機振動臺控制特性的影響[D]. 哈爾濱: 哈爾濱工業大學, 2011.