以三角形為背景的高考試題歸類解析

●

(馬寅初中學 浙江嵊州 312400)

●施哲明

(嵊州市教研室 浙江嵊州 312400)

三角形是最簡單的封閉幾何圖形．從小學、初中到高中，數學學習與三角形的聯系越來越緊密和頻繁，在數學的各種學習內容、各類試題背景中成為最活躍的幾何圖形之一．這個小小的三角形中充滿了無限的奧秘和變化：從最基本的3條線段、3個角的組成來看就包含著許多優美的性質，既有邊長關系，又有角度關系，還有邊角合一的正弦定理、余弦定理等等；若涉及中線、角平分線、垂線等，那更是到了一個神奇的三角王國；若再把它隱藏到某一些幾何圖形中，如圓錐曲線中的特征三角形、立體幾何中的線面角和面面角等，那更顯得豐富多彩，真可以說是三角、代數、幾何、圖形的百川交匯．正由于它在平凡中充滿著無窮的魅力，因此得到高考命題者的青睞．本文例舉若干以三角形為背景的試題，展現它在試題命制中的不同側面，供大家欣賞和參考．

1 定理為先，“邊角”互通

在高中數學中，三角形性質的代數化表達中，最重要的就是正弦定理和余弦定理，它們溝通了三角形的邊角關系，也提供了邊角相互轉化的工具．因此高考中有關三角形的試題最直接、最常見的就是應用正弦定理、余弦定理解決三角形中的有關度量問題．

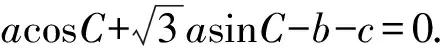
(1)求A；

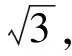
(2012年新課標全國數學高考試題第17題)

分析(1)由已知條件及正弦定理得

因為B=π-A-C，所以

得

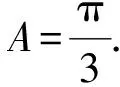
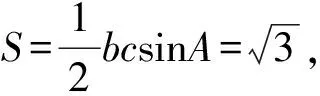
評析正弦定理和余弦定理是解決有關斜三角形邊角問題的2個重要定理，利用這2個定理可將邊角關系達到統一．本題第(1)小題求角，故需把邊轉化為角；第(2)小題求邊長，故需選用含3個邊長變量的余弦定理．在研究較復雜的三角形問題時，常需正、余弦定理綜合使用，甚至反復使用．

2 向量為“橋”，運算為“梁”

從向量進入高中數學后，三角形的幾何性質就可以用向量的形式來表現．既具代數表達形式又具非凡魅力的幾何意義的向量，在解決許多以三角形為背景的高考試題中，成為一道亮麗的風景線．

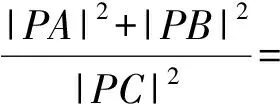
A．2 B．4 C．5 D．10

(2012年江西省數學高考試題第7題)

分析1以C為原點、CA，CB所在直線為x，y軸建立直角坐標系.設A(a,0)，B(0,b),則

從而 |PA|2+ |PB|2=

故選D．

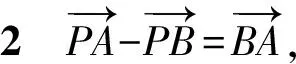
故選D．

分析3由平行四邊形性質得

故選D．

評析此題以直角三角形為背景呈現，初看似乎與平面向量無關，但倘若運用代數方法來解決此題會覺得無從入手，但一旦看清此題考查的真正意圖，再合理運用平面向量的運算，就能迎刃而解．真所謂是“不識廬山真面目，只緣身在此山中”．

( )

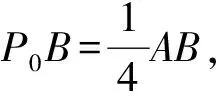
A．∠ABC=90° B．∠BAC=90°

C．AB=ACD．AC=BC

(2013年浙江省數學高考理科試題第7題)

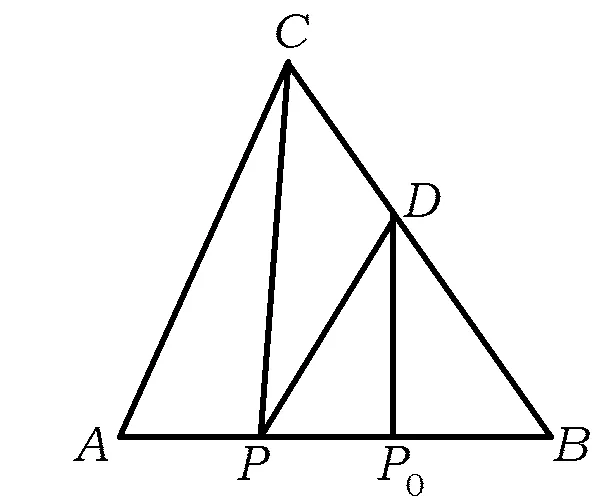
圖1

分析如圖1，在△ABC中，設BC的中點為D，則

同理可得

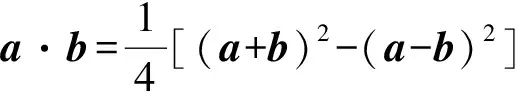
3 多“管”齊下，精彩紛呈

在高中數學中，涉及到三角形性質的試題，其表現形式往往是代數形態.而解決的主要手段，也是借助于三角、代數的方法．但在實際問題中，我們常常結合幾何圖形采用多種方法，從不同角度加以解決，這也恰好反映了三角形在高中數學中的魅力所在．

例4在△ABC中，AB=4，M為BC的中點，且AM=1，則∠BAC的最小值為______．

(2013～2014學年第一學期浙江省嵊州市高三期末檢測試題)

解法1(以所求∠BAC為目標)如圖2，由余弦定理得

a2=16+b2-8bcos∠BAC,

(1)

由式(2)，式(3)得

a2=4-16bcos∠BAC,

(4)

由式(1)，式(4)得

故∠BAC≥150°．

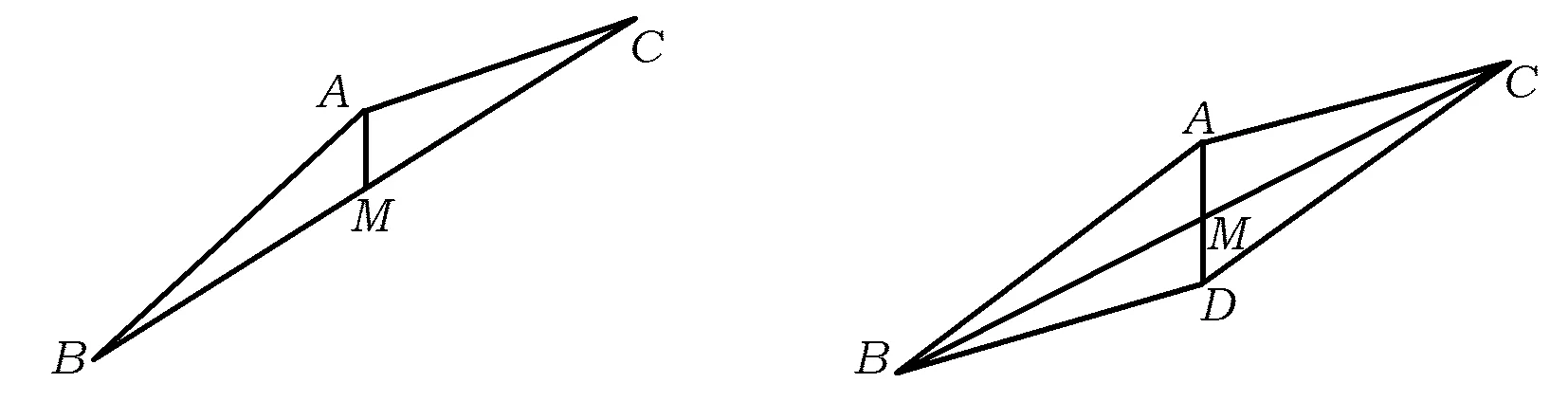
圖2 圖3

解法2(以所求角的補角∠ABD為目標)如圖3，延長AM到點D，使得AM=MD，聯結BD,CD.設∠ABD=θ，BD=x，則由余弦定理得

4=16+x2-8xcosθ，

即

故θ≤30°，從而∠BAC≥150°．

解法3在△ABD中，由正弦定理得

即

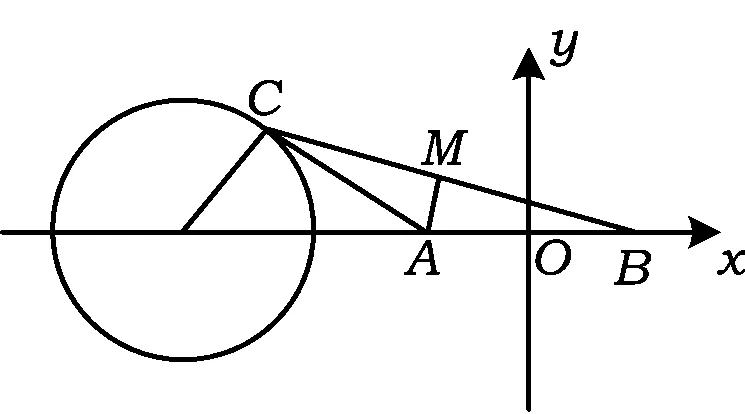
圖4

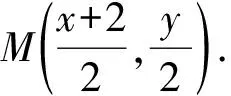
(x+6)2+y2=4，

這就是點C的軌跡．當AC與圓相切的時候，∠BAC的最小值為150°．

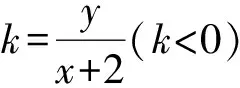
故∠BAC的最小值為150°．

解法6如圖5，延長BA到點Q，使得BA=AQ.因為點M為BC的中點，所以AM為QC的中位線，從而QC=2，即點C的軌跡是以Q為圓心、半徑為2的圓．故當AC與圓Q相切時，∠BAC的最小值為150°．

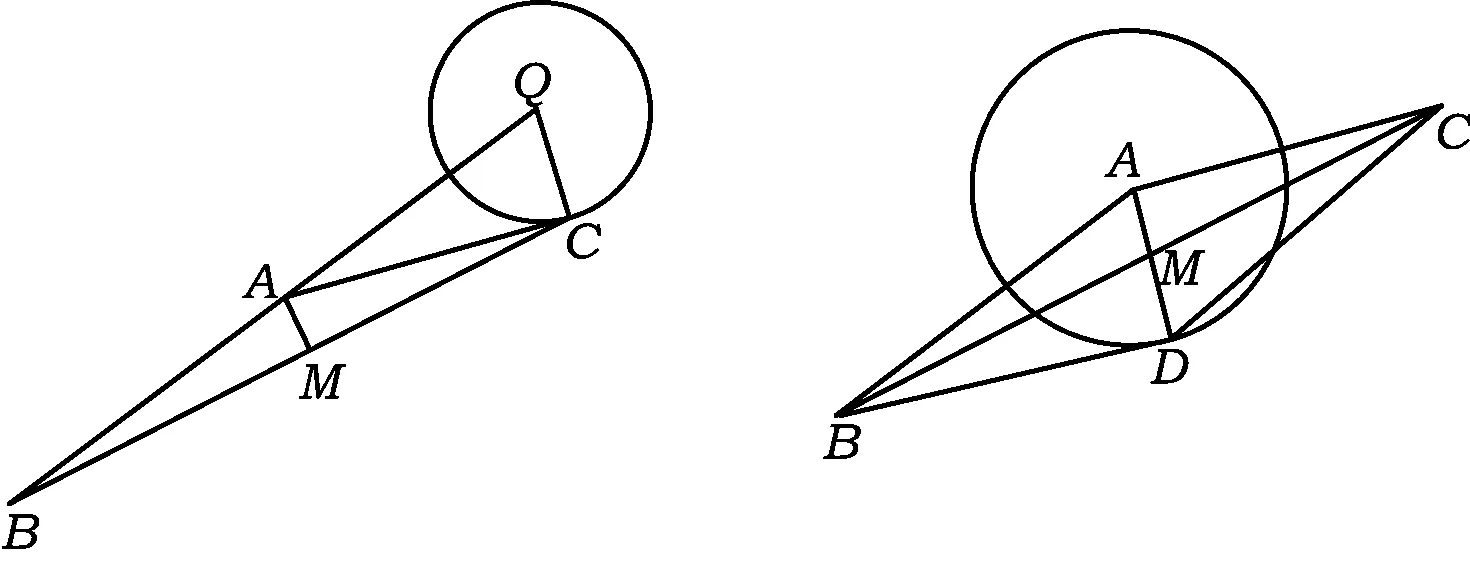
圖5 圖6

解法7(以中點M的軌跡為目標)如圖6，延長AM到點D，使得AM=MD.因為AD=2，所以點D在以A為圓心、半徑為2的圓上，當BD與圓相切時，∠ABD最大，從而∠BAC的最小值為150°．

評析運用三角、向量的代數運算和幾何運算、解析幾何、數形結合等多種數學方法，緊緊圍繞解題目標，展開了不同的解法，充分展示了三角形命題在高中數學中的復雜性和解法的多樣性、綜合性.本題無論從試題的命制，還是解法的呈現，都讓人賞心悅目，余味無窮．

4 置之于“形”，百花齊放

正如前面所述，三角形是最簡單也是最基本的平面封閉圖形,許多試題往往將它“鑲嵌”于其中，并以它作為背景、有機地融合了各方面的知識進行考查，形成了一批內涵豐富、立意新穎的試題．

( )

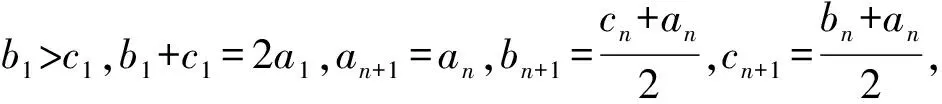
A．{Sn}為遞減數列

B．{Sn}為遞增數列

C．{S2n-1}為遞增數列，{S2n}為遞減數列

D．{S2n-1}為遞減數列，{S2n}為遞增數列

(2013年全國數學高考試題第12題)

分析通過邊長的遞推關系，得

結合an+1=an，可知點An在以Bn，Cn為焦點的橢圓上，且

故邊BnCn上的高逐漸增大.又因為|BnCn|=a1，所以{Sn}為遞增數列．

評析此題將三角形的頂點以遞推數列的動態形式給出，隱含圓錐曲線定義于其中，也不是通過簡單的高的變化來反映三角形的面積，而是通過相鄰2條邊的長度之間的關系來體現三角形的面積變化.在領略不凡新意的同時，對學生的邏輯思維能力和數學想象能力給予了深度的考查．

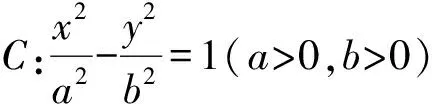
(2013年浙江省金華市高三月考試題第16題)

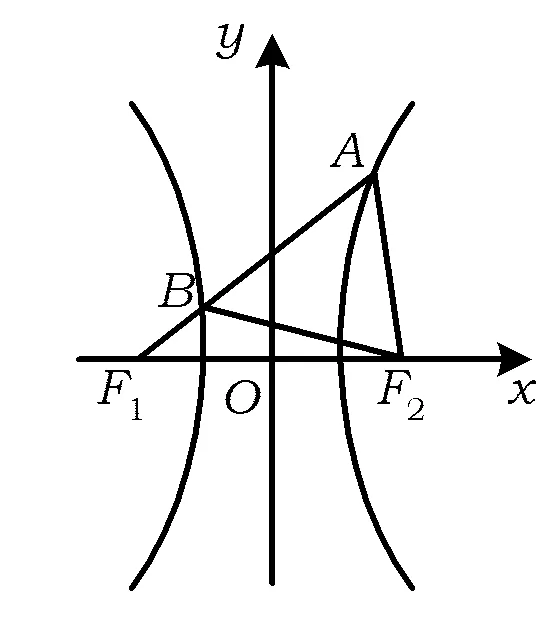
圖7

分析如圖7，依題意有

|BF1|= |AF1|-|AB|=

|AF1|-|AF2|=2a.

因為|BF2|-|BF1|=2a，所以

|BF2|=4a，

故

|AF2|=4a,|AF1|=6a.

又∠F1AF2=60°,|F1F2|=2c,由余弦定理得

4c2=36a2+16a2-2×6a×4a×cos60°=28a2，

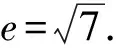
隨著學習階段的提升，有關三角形的試題的變化，表現特征為從幾何圖形及幾何性質向代數形式轉變，從單一的知識向綜合性知識轉變，從簡單背景向復雜背景轉變．這就需要教師在教學中，抓住三角形幾何性質的不同表現形式，綜合運用各種方法，靈活應用幾何結論，方能簡捷高效地解決新形式的三角形問題．