回歸教材 突出本質 注重核心 強調探究
——近3年福建省數學高考理科圓錐曲線綜合題分析及啟示

●

(連江第一中學 福建連江 350500)

圓錐曲線作為解析幾何的核心內容,一直是高考的重點與熱點,多以中、高檔題的形式出現,考查學生的分析問題與綜合解決問題的能力.縱觀近3年福建省數學高考理科圓錐曲線試題,平凡但不平淡,簡約而不簡單,強調數學本質,突出解析幾何的核心內容、基本思想及教育價值,充分發揮對中學數學教學的正確導向作用.本文試以高考圓錐曲線綜合題為例作些分析,期望對高三的復習教學有所幫助.

1 高考真題分析

1.1 眾里尋它千百度——驀然回首,那“題”卻在“教材”處

高考命題“源于教材,高于教材”,許多考題我們似曾相識,緣于其“根源”隱匿于教材例、習題當中,2013年福建省數學高考理科試題第18題就是一個典范.

例1如圖1,在正方形OABC中,O為坐標原點,點A的坐標為(10,0),點C的坐標為(0,10).分別將線段OA和AB十等分,分點分別記為A1,A2,…,A9和B1,B2,…,B9.聯結OBi,過Ai作x軸的垂線與OBi交于點Pi(其中i∈N*,1≤i≤9).

(1)求證：點Pi(其中i∈N*,1≤i≤9)都在同一條拋物線上,并求該拋物線E的方程；

(2)過點C作直線l與拋物線E交于不同的2個點M,N,若△OCM與△OCN的面積比為4∶1,求直線l的方程.

(2013年福建省數學高考理科試題第18題)

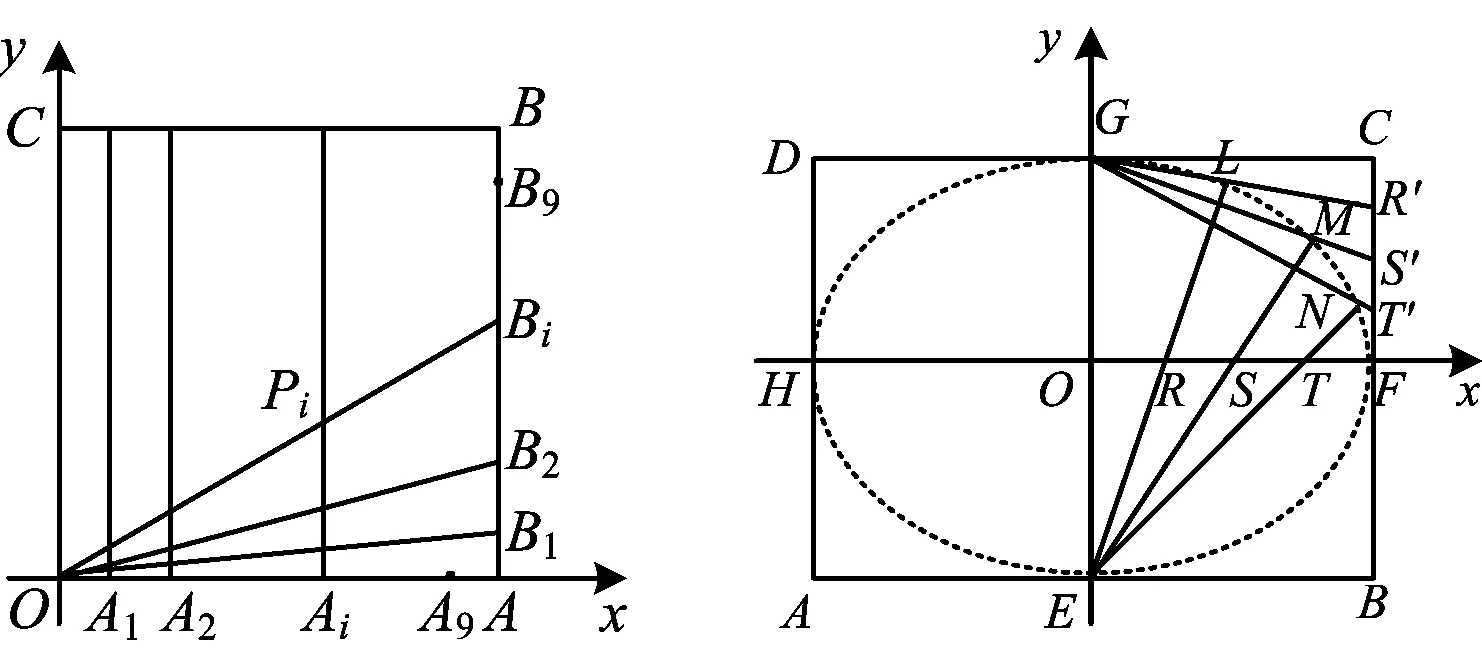
圖1 圖2

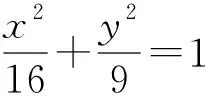
1.2 “知識”與“思想”齊飛——立足本質,滲透思想,強調教育價值

高考命題力求立足數學本質,從數學各分支的核心內容、學科思想以及相關分支的教育價值入手設置試題,合理地檢測學生的基本數學素養.其中解析幾何突出其“坐標法”的本質,要求考生將幾何問題代數化,并合理地運用代數手段解決幾何問題,體現解析幾何的基本思想,強調解析幾何的教育價值.

(1)求橢圓E的方程.

(2)設動直線l:y=kx+m與橢圓E有且只有一個公共點P,且與直線x=4相交于點Q.試探究：在坐標平面內是否存在定點M,使得以PQ為直徑的圓恒過點M？若存在,求出點M的坐標；若不存在,請說明理由.

(2012年福建省數學高考理科試題第19題)

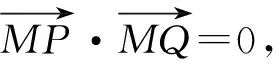
圖3 圖4

1.3 不畏浮云遮望眼——揭本探源,延伸拓展

高考探索性問題,往往隱藏著深刻的背景根源,只有深入研究,撥開“遮眼”的“浮云”,透過現象看本質,才能洞悉其中的“玄機”,領略美妙的意境.

(1)求雙曲線E的離心率.

(2)如圖4,O為坐標原點,動直線l分別交直線l1,l2于點A,B(A,B分別在第一、四象限),且△OAB的面積恒為8,試探究：是否存在總與直線l有且只有一個公共點的雙曲線E？若存在,求出雙曲線E的方程,若不存在,說明理由.

(2014年福建省數學高考理科試題第19題)

分析本題背景深刻,內涵豐富,這個“動中有定”、“變與不變”和諧共存的優美結論其實具有一般性,將試題結論推廣到一般情形,并研究其逆命題,可得如下結論：

圖5

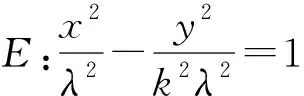
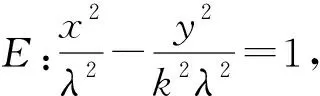
2 啟示

2.1 要實現從真正意義上回歸教材

教材是一種豐富的課程資源,是課堂教學中師生互動的橋梁,為教師的教和學生的學提供了大量有一定彈性的知識素材,更是學生開展思維活動、發展思維能力的主要載體.教材中的例題和習題都是經過專家反復考量的,具有很強的基礎性、示范性和可遷移性,并且內容豐富,題型多樣,反映相關數學知識的本質特征,蘊涵著豐富的思想方法和創新意識.高三復習教學不能摒棄教材而完全依賴于某些教輔用書,要實現從真正意義上回歸教材,以研究者的眼光,將一些看似簡單、入口較低而實際背景深刻、內涵豐富的例題和習題進行適當改編、延伸和拓展,開展探究性教學,以提高學生的思維探究水平和綜合解題能力,培養學生的創新意識,提升數學素養.

2.2 突出本質,注重核心,體現價值

“坐標法”作為解析幾何的本質,滲透了函數與方程、數形結合、分類討論、化歸轉化等重要思想.《普通高中數學課程標準(實驗)》指出解析幾何的核心內容包括幾何圖形的代數表示——點、直線、圓錐曲線的代數表示；常見幾何圖形、幾何性質的代數表示；利用代數研究直線、圓錐曲線及直線與圓錐曲線的關系與性質.其教育價值在于通過坐標法下幾何與代數統一性的認識,幫助學生建立普遍聯系的辯證觀念,發展學生的運算求解能力,拓展學生分析、解決問題的能力.因此,高三數學復習教學,必須貫徹課標理念,突出數學本質,關注學科各分支的核心內容,滲透重要的思想方法,并充分挖掘其教育價值,才能爭取較高的效益.

2.3 關注過程,重視探究

高考作為選拔性考試,著力于學生學習潛能與學科素養的考查,故經常設置一些開放性、探索性的試題,考查創新意識和探究精神.因此,高三教學要重視學生探究能力的培養,可以通過有目的地創設探究性問題情境,合理引導學生進行自主合作、交流探究活動,使學生親身經歷知識的發生與發展過程,體會蘊涵在其中的思想方法,領悟數學問題的本質,提高學生自主探究的能力,發展創新意識.

3 2個典型案例

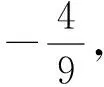
(人教版數學選修2-1第41頁例3)

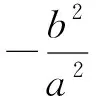
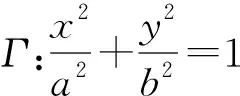
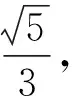
①求橢圓的方程；

②過點P(2,1)的2條直線分別與橢圓Γ交于點A,C和B,D,若AB∥CD,求直線AB的斜率.

(2)設P(x0,y0)為橢圓Γ內一定點(不在坐標軸上),過點P的2條直線分別與橢圓Γ交于點A,C和B,D,且AB∥CD,類比第(1)小題的第②小題直接寫出直線AB的斜率(不必證明).

(2014年福建省南平市高中畢業班適應性考試理科數學第19題)

圖6

分析本題第(1)題中第②小題涉及2條動直線及它們與橢圓相交得到的4個動點,顯得“變幻莫測”.常規思路通過聯立直線與橢圓的方程難以奏效.命題人提供的解法是先設出4個動點的坐標,再利用向量共線進行轉化,采用設而不求的思想求解,其中的整體代換及化歸思想的技巧性較強,運算相當繁瑣,難度較大.如果利用上述結論,則輕松獲解.如圖6,設點M,N分別是AB,CD的中點,則

由已知kAB=kCD,故kOM=kON,即點O,M,N共線.由平面幾何知識易證點P也在MN上,故kOP=kOM,從而

案例2已知直線y=x-2與拋物線y2=2x相交于點A,B.求證：OA⊥OB.

(人教版數學選修2-1第73頁第6題)

問題1(探究原題的一般性結論)直線l過點(2p,0),且與拋物線y2=2px(其中p>0)交于點A,B(異于坐標原點O),求證：OA⊥OB.

問題2(探究原題的逆命題)已知直線l與拋物線y2=2px(其中p>0)交于點A,B(異于坐標原點O),且OA⊥OB,求證：直線l恒過點(2p,0).

問題3(進一步推廣探究)已知點M是拋物線上任意的一個已知點,直線l與拋物線y2=2px(其中p>0)交于點A,B(異于點M),若MA⊥MB,試探究直線l是否恒過定點.

應用已知雙曲線C的中心在原點且經過點D(2,0),m1={2,1},m2={2,-1}分別是2條漸近線的方向向量.

(1)求雙曲線C的方程；

(3)雙曲線C或拋物線y2=2px(其中p>0)是否也有類似第(2)小題的結論？若是,請選擇一個曲線寫出類似結論(不要求書寫求解或證明過程).

(2014年福建省福州市高三模擬試卷第19題)

分析上述案例通過對2道教材例、習題進行縱向挖掘和橫向拓展,推廣得到一系列有用的一般性結論,不僅使一些高考模擬題輕松獲解,而且開拓了學生的視野,激活了學生的思維,培養了學生的自主探究能力,提高了學生的創新意識.

4 結束語

數學教育家弗賴登塔爾和克萊因極力倡導教師通過對教材進行“再創造”激發學生的學習動機,使學生積極主動地參與數學知識的發現,親身經歷數學創造的過程.通過本文,筆者認為,高三教師要將教材視為復習用題的“根據地”,加強對教材例題、習題的整合歸類、挖掘提升、變式拓展,以充分發揮其教育功能；研究高考試題,努力探尋考題在教材中的原型,實現高考試題與教材的無縫對接,徹底摒棄脫離教材的“題海戰術”,實現高效的復習教學活動.

參 考 文 獻

[1] 陳中峰.體現解析幾何核心內容及教育價值的高考試題賞析[J].中學數學(高中版),2013(6)：92-95.

[2] 李鋒.2013年高考福建理科數學第18題賞析[J].福建中學數學,2014(1/2)：17-20.

[3] 中華人民共和國教育部制訂.普通高中數學課程標準(實驗)[M].北京:人民教育出版社,2003.