一道數學高考試題的多元透析

●

(嘉興高級中學 浙江嘉興 314031)

1 問題的提出

2014年浙江省數學高考文科試題第16題，條件簡潔,問題清楚，但學生普遍感覺比較“難”，或無從下手，或因思路不清、計算困難等半途而廢.本文試圖從不同的視角出發，列舉學生采用的幾種常規解法進行障礙診斷、評析與題源探究，同時，給出高觀點下的再審視，提出幾點教學反思與改進.

例1若實數a,b,c滿足a+b+c=0，a2+b2+c2=1，則a的最大值為______.

(2014年浙江省數學高考文科試題第16題)

2 常規解法

2.1 函數的視角

解法1由條件a+b+c=0，得

c=-(a+b)，

代入a2+b2+c2=1，整理得

(1)

由求根公式解得

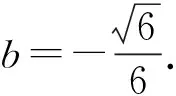
2.2 方程的視角

解法2由解法1的分析，得

即

從方程的視角，此式可看作是關于b的一元二次方程，因方程有解，故Δ≥0，即

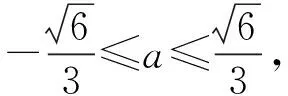
2.3 不等式的視角

結合不等式(b+c)2≤2(b2+c2)，得

a2≤2(1-a2)，

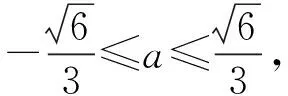
3 診斷、評析與探究

3.1 障礙診斷

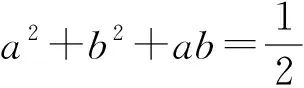
因感覺離目標很遙遠而止步，殊不知，在此基礎上，運用基本不等式，消去b和c，便有如下的解法：

將b+c=-a代入得

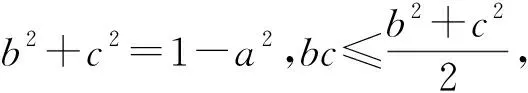
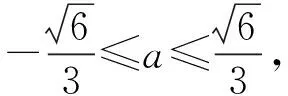
至于解法3，很多學生也會想到用基本不等式去解，但他們的經驗往往是會解決只含有“二元”、直接用基本不等式即可解決的問題，如例2和例3.

例2若實數x,y滿足x2+y2+xy=1,則x+y的最大值為______.

(2011年浙江省數學高考文科試題第16題)

例3若正實數x,y滿足2x+y+6=xy,則xy的最小值為______.

(2010年浙江省數學高考文科試題第15題)

從本質上看，例2、例3和例1是相同的，均是已知2個或3個變量間的關系，求其中1個變量(或2個變量的組合)的最值.

可見，學生感到此題“難”，是因為所給的條件a+b+c=0，a2+b2+c2=1中所含的變元有3個，而平時常見的變元只有2個.究其原因，還是沒有領會好“消元”這一最基本的思想方法.

3.2 評析

以上3種解法，都基于一種最自然、最樸素的思想方法，即消元，以達到減少變元、化繁為簡、化多為少的目的.視角1通過消元，化“三元”為“二元”,化“二元”為“一元”，最終將問題化歸為一元函數的最值問題，雖道路曲折，但目標明確.視角2通過消元，抓住方程的定義(即含有未知數的等式)，將問題化歸為一元方程的有解問題.視角3借助不等式，通過整體消元，將問題化歸為一元不等式的求解問題，簡潔明了.可見，函數、方程、不等式等是解決此題的基礎知識，但要成功解決，還需理清題意，抓住本質，運用消元的思想方法.

3.3 題源探究

探究發現，消元的思想方法在浙江省歷年高考卷或模擬卷中屢見不鮮，在各大名校的自主招生考試中也時常出現，比如：

例4若正數x,y滿足x+3y=5xy,則3x+4y的最小值為

( )

(2012年浙江省數學高考文科試題第9題)

解法1(“1”的代換)

由x+3y=5xy，得

故

展開并結合基本不等式，得

教學時，教師常常局限于這種“高技巧”的展示，卻忽視了最基本的思想方法.其實，例4和例1有相似的地方，仍可用上面2個“樸素”的方法解決.

解法2(函數的視角)

從函數的視角，z=3x+4y為二元函數，通過消元，轉化為一元函數.由x+3y=5xy，得

從而

解法3(方程的視角)

從方程的視角，x+3y=5xy為二元方程，通過消元，轉化為一元方程.令3x+4y=t,得

代入方程，化簡整理得

15x2-(5+5t)x+3t=0.

此方程可看作是關于x的一元二次方程，方程有解，故Δ≥0，即

(5+5t)2-180t≥0，

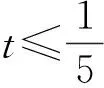
(3x+4y)min=5.

4 高觀點下的再審視

對于例1,還在如下的解法:

4.1 參數方程的視角

解法5由解法2的分析，知

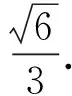
解法6由a2+b2+c2=1，得

b2+c2=1-a2.

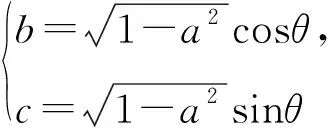
a=-(b+c)，

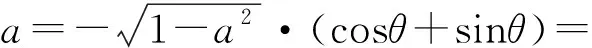
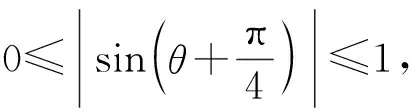
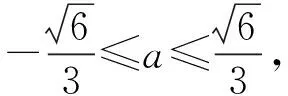
4.2 非線性規劃的視角

解法7由解法1的分析，知

令a=-x-y，b=x-y,代入得

2x2+6y2=1.

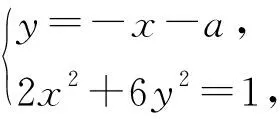
8x2+12ax+6a2-1=0，

令Δ=0，得 (12a)2-32(6a2-1)=0，

4.3 柯西不等式的視角

解法8由解法7的分析，知

2x2+6y2=1，

由二維柯西不等式，得

即

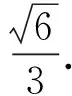
4.4 平面解析幾何的視角

解法9由解法3的分析，知

即

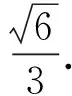
4.5 空間解析幾何的視角

代入化簡得

2z2+2tz+2t2-1=0，

令Δ=0，得

4t2-8(2t2-1)=0，

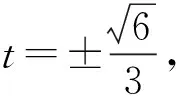
5 教學反思與改進

一道所謂的難題，經過不同視角下的透析與再審視，其實問題簡潔，解法自然，讓人回味，發人深省.同時也激勵我們反思自己的數學課堂教學，改進教師的教學行為和學生的學習習慣.

5.1 重結果、更重過程

新課程理念強調“學生的積極參與，重視學生的體驗，關注知識的發生、發展過程”.如學生在學習“基本不等式”時，不僅要知道它的結論，更要理解它的推導過程，關注它所蘊含的幾何意義、產生的背景以及簡單應用.又如在解題教學中，教師不僅要關注學生解題結果的正確與否，還要關注他們的思維過程.特別是在那些學生易錯、易漏、不嚴謹、欠規范或對知識的理解出現偏差或錯誤的要害處，更要讓學生去體驗，引導他們去交流、討論，在思維的碰撞中，讓錯誤充分暴露，甚至有時可以將錯就錯、以錯糾錯，自然地達到“示錯、知錯、改錯”的目的.必要時，教師可以加以點撥或評價，幫助學生認識各種思路的優劣，解法的長短，和學生一起探求最優解.這樣，學生在“動腦、動手、動口”的積極參與中得到體驗、感悟.

5.2 重知識、更重能力

新課程理念強調“注重提高學生的數學思維能力”.對學生而言，有用的不僅是數學知識，更重要的是數學思維能力.因此在教學中不僅要重視知識的形成過程，還要在數學知識發生時，重視挖掘它所蘊含的思想方法，提高學生分析問題、解決問題的能力.重知識，主要表現在重知識間的邏輯聯系，如基本不等式與柯西不等式間的聯系，不等式與函數、方程的聯系等.這樣，通過內部的聯系，把握知識的本質，并從中培養學生類比、抽象、概括等思維能力.

5.3 輕技巧、重通性通法

高考是對學生學習過程和水平的檢驗，現行的高考試卷計算量較大，要求在規定時間內完成，對有些學生來說是有一定困難的，掌握一定的解題技巧也是有必要的.但是，技巧往往有一定的局限性，有時難以想到，沒有普適性.因此，在平時的解題教學中，我們更應引導學生去分析思維的起點與突破口.注重知識間的邏輯聯系，講“套路”，更講“套路”背后所蘊含的最基本的數學思想方法(如本題中所涉及到的消元的方法、函數與方程的思想、化歸的思想、數形結合的思想等)，讓通性通法成為學生解題的“家常菜”.

5.4 尊重差異、關注個性

新課程理念倡導“建立新型的師生關系，教師要尊重學生間的差異，關注學生個性的發展”.如果說例1中的前4種是“大眾化”的常規解法，可以讓所有學生都“吃得飽”，那么，后6種“高觀點”下的解法，則可以讓優秀學生“吃得好”.這些“高觀點”下的視角和解法，有些是必修內容的拓展，有些是選修內容，還有些涉及到高等數學的有關內容，對大多數學生可不作要求，但對于那些感興趣的學生可以適當“加餐”，或根據他們自己的愛好和需求，鼓勵他們來點“自助餐”.

浙江省新一輪課改加強了選修課程的地位，也正是基于“提供多樣課程，適應個性選擇”這一理念，我們何不借課改的春風，讓必修課程校本化多一點，讓選修課程特色化多一點，讓必修、選修課程一體化多一點呢？例如，針對那些喜愛數學或者今后想在理工科有關專業發展的學生，是不是可以嘗試開設“高觀點下的高中數學”、“奇思妙想的數學世界”等選修課呢？這樣，學生的興趣才能得以提高，個性才能得以彰顯，思維能力才能得以發展，我們的教學才能為學生的“終身學習、終身發展”奠定堅實的基礎.

6 結束語

羅增儒教授曾說：“數學解題無禁區，數學教學有講究”.我們在數學教學中，有意積累知識環、方法鏈，讓知識環環相扣、方法鏈鏈相連，學生才可以做到舉一反三、觸類旁通，唯有如此，我們的教學才能減負.重知識的建構，更重思維的提升和能力的培養，引領學生積極參與，把握知識的本質，體味其蘊含的思想方法，唯有如此，我們的教學才能“增效”.關注學生學習數學的水平，更關注他們在活動中所表現出來的情感、態度和價值觀的變化，唯有如此，新課程理念才能落到實處.筆者認為，這正是新形勢下數學教師應努力追求的.

參 考 文 獻

[1] 王劍明.方程思想與判別式法[J].中學教研(數學),2013(3):9-12.

[2] 李金興.2013年數學模擬卷(二)[J].中學教研(數學),2013(2):46-47.

[3] 中華人民共和國教育部.普通高中數學課課程標準(實驗)[M].北京：人民教育出版社，2004.

[4] 羅增儒.數學解題學引論[M].西安：陜西師范大學出版社,2001.