別樣風景
——中考尺規作圖題新探
●
(湖州市第五中學教育集團 浙江湖州 313000)
《課程標準(2011年版)》(以下簡稱《課標》)指出:“在尺規作圖題中,了解作圖的道理,保留作圖的痕跡.”這就是說要讓學生了解尺規作圖中作法的來龍去脈,其意義在于使學生更好地理解幾何語言,提升邏輯推理能力,積累數學活動的經驗,培養空間觀念.正如史寧中在《義務教育數學課程標準(2011年版)解讀》中指出:“作圖也要做到有根有據……這種要求有助于發展學生的理性精神,應當予以重視.”2013年和2014年的中考題中關于尺規作圖的命題呈現出不少的“新意”和“深意”.為釋其意,筆者舉例如下,并嘗試從教學的角度提出針對性建議,不當之處請同仁斧正.

圖1
1 命題形式與賞析
1.1 不給作法,按要求作圖并利用所作圖形計算
例1實踐操作如圖1,△ABC是直角三角形,∠ACB=90°,利用直尺和圓規按下列要求作圖,并在圖中標明相應的字母(保留作圖痕跡,不寫作法).
(1)作∠BAC的角平分線,交BC于點O;
(2)以O為圓心、OC為半徑作圓.
綜合運用在你所作的圖中,
(1)AB與⊙O的位置關系是______(直接寫出答案);
(2)若AB=13,BC=12,求⊙O的半徑.
(2013年江蘇省鹽城市數學中考試題)
點評此題作圖并不難,難點在于如何利用所作圖形解答綜合運用中的2個小題,考查了直線與圓的位置關系、勾股定理和面積法.
賞析1本題一改過去只要求學生根據要求動手作圖的單一命題思路,而是先作圖再結合圖形進行推理運算.縱觀近2年來的中考尺規作圖題,此類先作圖后計算的題型為數不少,體現了“四基”中提出的“基本數學活動經驗”.這里考查尺規作圖倒是其次,更重要的是體現了以形引數的命題思路,真可謂“醉翁之意不在酒”.
1.2 給出作法和圖形并保留痕跡,依據所得圖形證明
例2如圖2,小紅在作線段AB的垂直平分線時,是這樣操作的:分別以點A,B為圓心、大于線段AB長度一半的長為半徑畫弧,相交于點C,D,則直線CD即為所求.聯結AC,BC,AD,BD,根據她的作圖方法可知,四邊形ADBC一定是
( )
A.矩形 B.菱形
C.正方形 D.等腰梯形
(2014年浙江省麗水市數學中考試題)
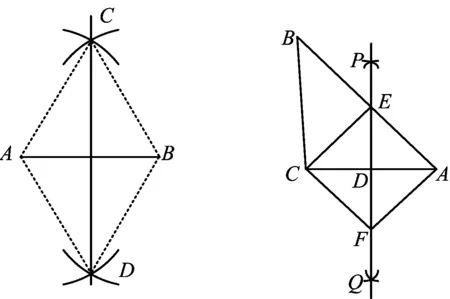
圖2 圖3
例3如圖3,已知△ABC,按如下步驟作圖:

②作直線PQ,分別交AB,AC于點E,D,聯結CE;
③過點C作CF∥AB交PQ于點F,聯結AF.
(1)求證:△AED≌△CFD;
(2)求證:四邊形AECF是菱形.
(2014年新疆維吾爾自治區數學中考試題)
點評同樣是垂直平分線的尺規作法,以上2個例子的命題形式卻迥然不同.不禁讓人聯想到一題多解、一圖多用,上述2個例子可謂“一法多題”.
賞析2以上2個例子將尺規作圖與幾何證明“雙劍合璧”,主要考查學生認識與理解作法.利用作圖結論進行幾何演繹推理的能力,為近2年來中考尺規作圖題命題思路之主旋律,此種命題方式給人以“珠聯璧合,相得益彰”之感.
1.3 給出作法和圖形并保留痕跡,依據所得圖形推理計算
例4如圖4,以△ABC的頂點A為圓心、以BC長為半徑作弧;再以頂點C為圓心、以AB長為半徑作弧,2條弧交于點D;聯結AD,CD.若∠B=65°,則∠ADC=________.
(2013年吉林省長春市數學中考試題)

圖4 圖5
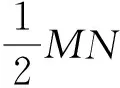
( )
A.a=bB.2a+b=-1
C.2a-b=-1 D.2a+b=1
(2013年湖北省咸寧市數學中考試題)

圖6 圖7
例6小敏在作⊙O的內接正五邊形時,先做了如下幾個步驟:
①作⊙O的2條互相垂直的直徑,再作OA的垂直平分線交OA于點M,如圖6;
②以M為圓心,BM長為半徑作圓弧,交CA于點D,聯結BD,如圖7.
若⊙O的半徑為1,則由以上作圖得到的關于正五邊形邊長BD的等式是
( )

(2013年浙江省紹興市數學中考試題)
點評以上3個例子以尺規作圖為背景知識,或建立圖形推理運算,或融合坐標、方程等數學思想,考查學生綜合運用所學知識解決數學問題的能力,具有一定的區分度.
賞析3由上3個例子可見中考尺規作圖命題逐漸向對作法的理解與綜合運用的思路上轉變,已成為近2年來的一種命題趨勢.上述3個例子一般都給出大段作法,直至讀到最后才理清整個題目的概貌(如例6),可謂“千呼萬喚始出來”.
1.4 給出作法和圖形并保留痕跡,依據作法判斷結論正誤

( )
A.射線OE是∠AOB的平分線
B.△COD是等腰三角形
C.點C,D關于OE所在直線對稱
D.點O,E關于CD所在直線對稱
(2013年云南省曲靖市數學中考試題)

圖8 圖9
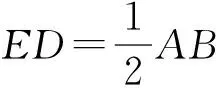
( )
A.①②③ B.①②④
C.①③④ D.②③④
(2014年浙江省湖州市數學中考試題)
點評同樣是給出作法和保留痕跡,上述2個例子的命題思路并不拘泥于推理運算和演繹證明,而是給出多種關于所作圖形的結論,考查學生明辨作法是非的能力.尤其是例8,并不是完整的中垂線尺規作圖,實質上卻作出了BC的中垂線PD,這就需要學生有理解作法的數學本質結構的能力.
賞析4這類題型從一些基本作圖出發,但并不僅僅停留在基本作圖層面,而是圍繞這些基本作圖進行改頭換面.比如例7添加一條線段CD,例8只呈現基本作圖的部分作法步驟.不得不說,這里似乎呈現出一種“似曾相識燕歸來”的命題取向.
1.5 給出保留痕跡的圖形,推斷某些作法或依據

( )

圖10
A.以點B為圓心、OD為半徑的圓
B.以點B為圓心、DC為半徑的圓
C.以點E為圓心、OD為半徑的圓
D.以點E為圓心、DC為半徑的圓
(2013年江蘇省南通市數學中考試題)
點評該例直接考查學生對“作一個角等于已知角”的某一步作法的理解,應該說難度不大,但若未深入學習、理解,則易出錯.
賞析5由于《課標》弱化了對作圖的理論證明且不要求寫出作法,此類題型在近幾年的尺規作圖題中不多見,大都來自于《課標》規定的基本作圖.這類題型考查尺規作圖作法的依據,呈現出一種反璞歸真的命題取向,真可謂“問渠哪得清如許,為有源頭活水來”.
1.6 給出多種作法,按要求判斷作法正誤
例10已知:線段AB,BC,∠ABC=90°.求作:矩形ABCD.
以下是甲、乙2位同學的作業:
甲: (1)以點C為圓心、AB長為半徑畫弧;
(2)以點A為圓心、BC長為半徑畫弧;
(3)2條弧在BC上方交于點D,聯結AD,CD,四邊形ABCD即為所求(如圖11).
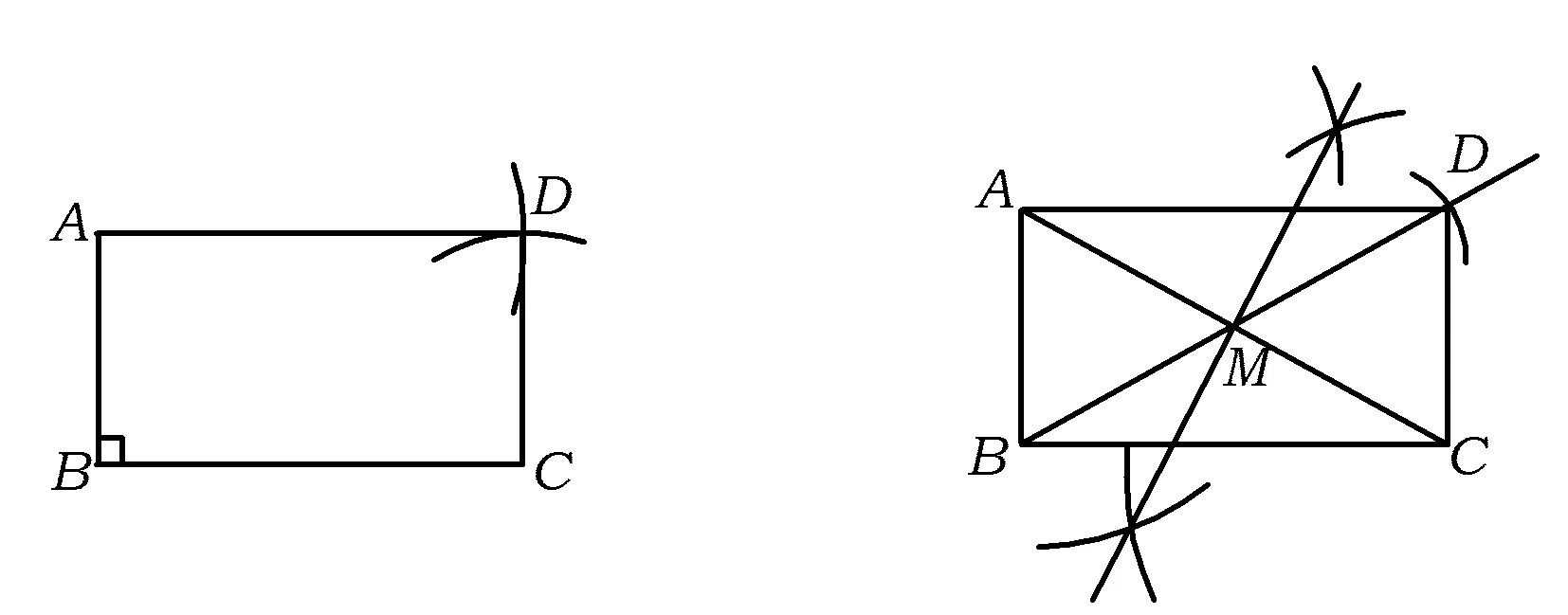
圖11 圖12
乙:(1)聯結AC,作線段AC的垂直平分線,交AC于點M;
(2)聯結BM并延長,在延長線上取一點D,使MD=MB,聯結AD,CD,四邊形ABCD即為所求,如圖12.
對于甲、乙的作業,下列說法正確的是
( )
A.兩人都對 B.兩人都不對
C.甲對,乙不對 D.甲不對,乙對
(2013年河北省數學中考試題)
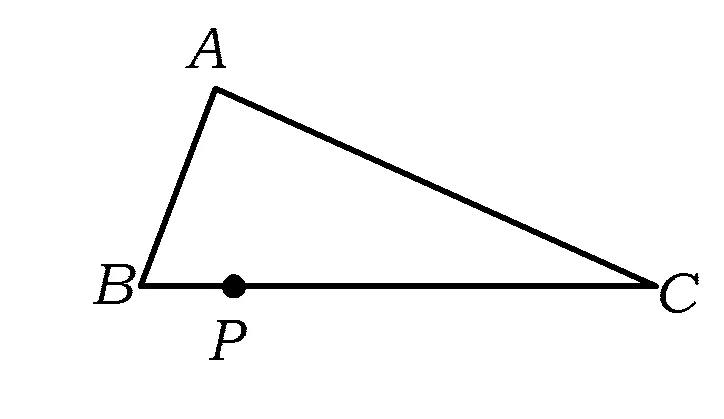
圖13
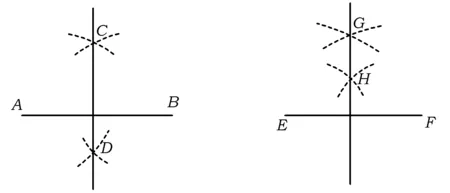
例11如圖13,已知△ABC(AC ( ) A. B. C. D. (2014年河北省數學中考試題) 點評例10詳細地給出了2種不同的作法,把作法的正確性問題拋給學生,就是要求學生在平時的學習中要“了解作圖的道理”,理解作法中的語言并運用.例11則直接給出了4個保留痕跡圖,要求學生按要求依據圖中所保留的痕跡來識別選擇一種正確的方法,可謂匠心獨運. 賞析6這2道例題同出河北,一改過去只要求學生能夠掌握基本作圖并深諳其道地運用解作圖題的命題思路.現在的命題減少了要求學生作圖的部分,而直接給出多種保留痕跡的圖,要求學生根據作法來推斷、證明,這種尺規作圖的命題趨勢值得注意.如果沒有對尺規作圖作法的深刻認識和其他幾何知識的獨到理解,這樣的題目對學生來說也并不輕松.這類題型讓作法本身成為考查手段,命題方式給人無限遐想空間,似有意境幽遠之感,真可謂“曲徑通幽處,禪房花木深”. 課改至今關于尺規作圖的教學要求也幾經變遷,相對2005年的課標,2011年版的課程標準對尺規作圖提出了更高的要求,具體如下:(1)進一步完善了基本作圖的要求,增加了過一點作已知直線的垂線;(2)增加了直角三角形的作圖;(3)提高了與圓有關的作圖要求;(4)明確規定尺規作圖的要求——弱化了作圖的理論證明,只需保留作圖痕跡,不要求寫出作法. 誠然,我們平時教學中不強調寫作法而只求保留痕跡,看似降低了要求,學生在作業中的表現也不錯,但在遇到上述題型時卻往往差強人意,筆者以為這與沒有充分理解作法的本質不無關聯.因此,在教學中教師應當創造機會讓學生說作法、想作法、議作法.對于基本作法應進行一定的板演、示范,甚至應當考慮在教基本作圖時要求學生寫出作法.這就好比書法入門者必先從基本的一筆一畫和熟讀顏、柳、趙、王等各種名家字帖學起一樣,待到可以將字形的體態、結構和筆法熟諳于心時方可做到運用自如乃至力透紙背、行云流水. 教師在平時的教學中注重作圖技能教學的同時,更應注重教學生理解作法的數學本質.也就是說,教師不僅要教作圖的技能,而且要教對作法的理解、闡釋與運用,讓學生懂得一種作法的數學本質結構及其聯系,以點帶面形成體系,從而貫通整個初中平面幾何.如作一條線段的中點,一方面,這個基本作圖同樣可用于作一條線段的中垂線、一個三角形的中線、過一點作已知直線的垂線、已知2條線段作以這2條線段為對角線的菱形等;另一方面,作線段中點本質上來說是依據中垂線定理逆定理作圖的,因此,又能產生一些非常規的作法,如圖14和圖15.尺規作圖中像這樣能夠揭示數學本質結構的例子還有許多.波利亞曾說:“一個專心、認真備課的老師往往能夠拿出一個有意義但又并不復雜的題目,去幫助學生挖掘問題的各個方面,使得通過這道題,就好像通過一道門,把學生引入一個完整的理論領域.”這樣看來尺規作圖教學就猶如那道題,而整個平面幾何領域就是那個“完整的理論領域”. 圖14 圖15 近讀有關數學慢化教育的文章,如《中學數學教學參考》2014年第1~2期刊登了2篇題為《人文學習時代下的數學慢教育——“圖形的平移”教學設計與思考》、《拉長過程慢中求真——“求根公式”的案例設計》,并向全國征稿討論.筆者以為在尺規作圖的教學中急需這樣的慢教育,現行課標雖不要求寫作法,但增加了“了解作法的道理”,這對教師的教學提出了更高的要求,那些只傳授怎么做,而不講明其中原由和不講解其他作法的尺規作圖教學時代將一去不返,取而代之的是注重學習過程的經歷,注重作法的理解與運用,注重學生操作、體驗和感悟,注重“再發現”、“再創造”的教學大行之道. 參 考 文 獻 [1] 劉芳.對尺規作圖教學的三個思考[J].中學數學雜志,2009(10):11-13. [2] 高波.明理得法 水到渠成——以“作一個角的平分線”為例淺析初中尺規作圖教學[J].中學數學,2013(1),18-20.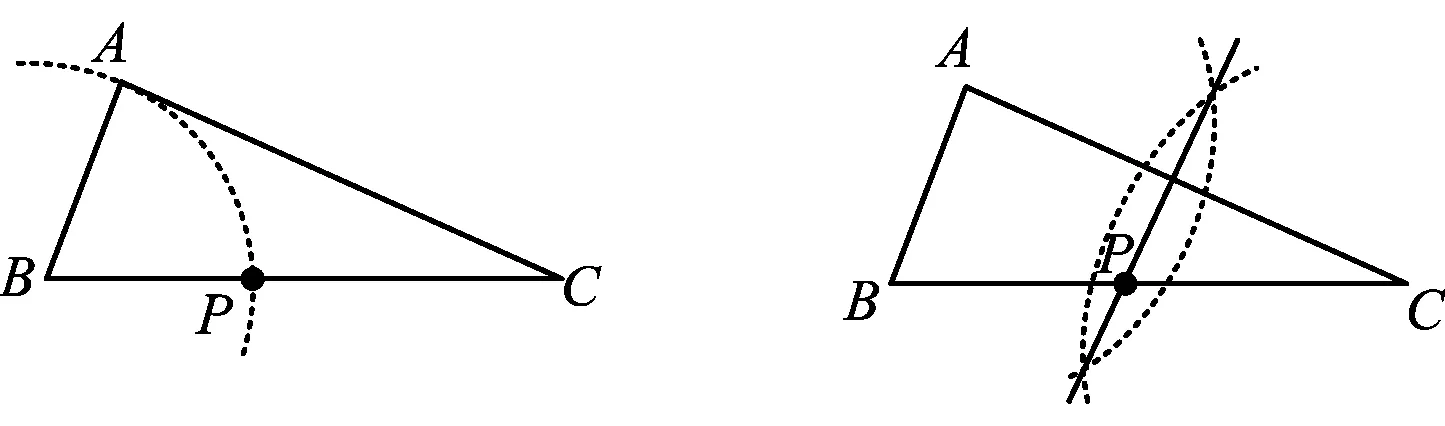
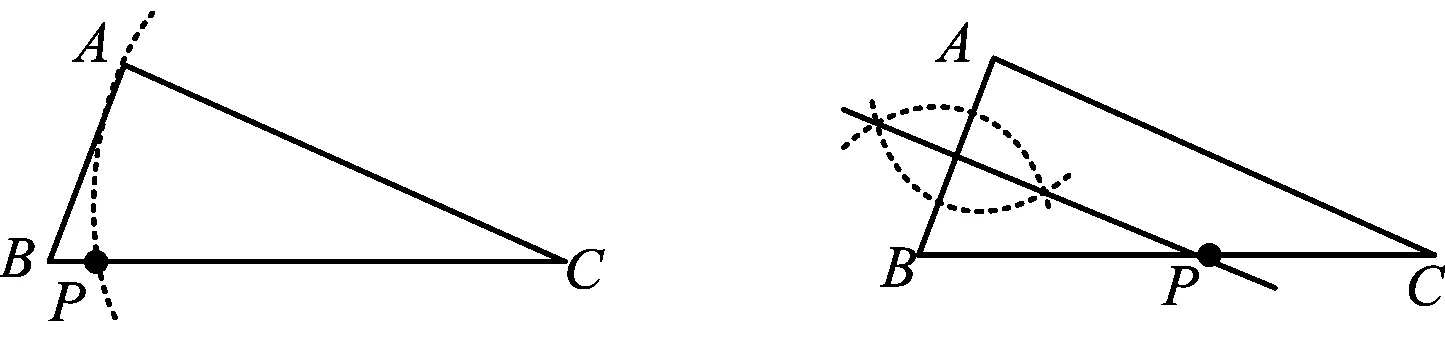
2 對教學的啟示
2.1 對作法的教學建議
2.2 對數學本質結構教學的啟示
3 寫在最后

