三人行 必有我師
——同伴互助式數學教師專業發展

●

(寧波中學 浙江寧波 315100)

●楊樟松

(衢州第二中學 浙江衢州 324000)

俗話說:“要給學生一杯水，教師得有一桶水.”可見教師自身的專業素養的重要性.那么如何提高教師的專業素養呢？為此學校、教育局每年都為教師提供各種各樣的培訓．但要從根本上提高教師的專業素養還是要靠日積月累，反思日常教學中的點點滴滴.波斯納提出“教師的成長=經驗+反思”，就是一條教師的專業成長之路．教師的專業發展需要教師成為反思型、學習型、創新型人才，而同伴互助、相互交流，是實現這個目標的一條好途徑．

1 提出問題,直觀解答

在解決數學問題和數學教學過程中我們總會遇到一些困惑，而這些困惑在大家的討論中總可以得到解決，我們也能從中得到啟迪．在同伴互助的過程中,教師的專業素養得到了發展．

某一天，教師A提出了一個關于空間軌跡的問題．

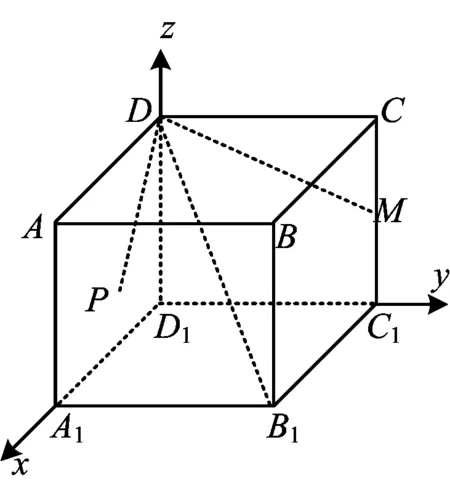
圖1

問題如圖1，已知正方體ABCD-A1B1C1D1，點M是棱CC1的中點，P是平面ABB1A1內的點，且滿足∠PDB1=∠MDB1，則點P的軌跡是

( )

A．圓 B．橢圓

C．拋物線 D．雙曲線

教師X的想法是：當截面與圓錐的一條母線平行時，截得的曲線是拋物線．因為滿足∠PDB1=∠MDB1的點P的軌跡在以DB1為軸、軸截面頂角為2∠MDB1的圓錐面上，又點P在平面ABB1A1內，所以點P的軌跡是平面截圓錐所得的曲線．又因為DM∥ABB1A1，所以點P的軌跡是拋物線．

2 得出矛盾，另辟蹊徑

然而參考答案是D，即軌跡是雙曲線．于是教師J也來參與這個問題的討論．

教師J采用空間向量的方法解決了它．如圖1，建立空間直角坐標系D1-xyz，設正方體棱長為2，且P(2,x,y)，則

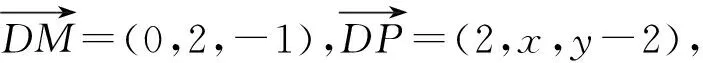
由于∠PDB1=∠MDB1，由向量夾角公式得

代入坐標得

整理得

2x2+5xy+2y2-20x+2y-4=0,(1)

對于方程Ax2+Bxy+Cy2+Dx+Ey+F=0，當Δ=B2-4AC<0時，方程代表的曲線是橢圓；當Δ=B2-4AC>0時，方程代表的曲線是雙曲線；當Δ=B2-4AC=0時，方程代表的曲線是拋物線．而方程(1)中

Δ=52-4×2×2=9>0，

因此點P的軌跡是雙曲線．當然也可作旋轉變換

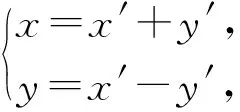
代入整理得點P的軌跡方程為

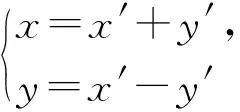
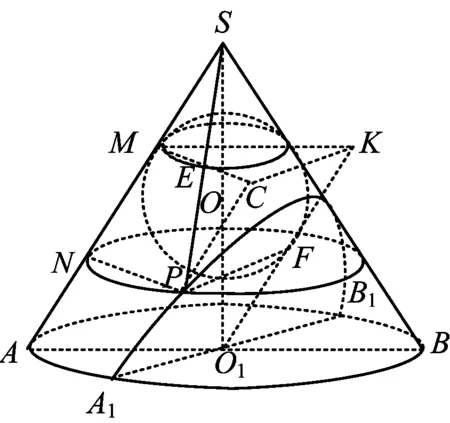
圖2

3 生疑釋疑，再得矛盾

由此得出了2個矛盾的答案，但是好像都找不到各自解題的破綻．于是教師C也加入這個研究行列．教師C首先肯定了教師X的想法，并給出了如下結論：

結論如圖2，已知A1B1⊥AB，O1K∥母線SA，A1B1與O1K構成的截面設為α，可證平面α截圓錐所得曲線為拋物線．

證明設P為截線上一點，在圓錐內部放1個球O，使得它與圓錐側面和截面α相切，球O與截面α切于點F，與母線SA切于點M，作MK∥AB交O1K于點K，過點M作平行于底面的平面交SP于點E，過點P作平行于底面的平面β交母線SA于點N，在平面α內作CK⊥O1K，K是垂足，過點P作CK的垂線，交CK于點C，聯結MC，則PC∥O1K∥SA．因為A1B1⊥AB,A1B1⊥SO1，所以A1B1⊥平面SAO1，從而A1B1⊥SA.又因為O1K∥SA，得A1B1⊥O1K，又CK⊥O1K，所以CK∥A1B1，從而平面MCK∥底面，所以平面MCK∥平面β．平面MNPC與平面MCK、平面β分別交于MC,NP，從而MC∥NP，于是四邊形MNPC是平行四邊形，故MN=PC．

又因為MN=PE(圓臺的母線長相等)，PE=PF(球外一點的切線長相等)，從而PF=PC，即曲線上任意一點P到定點F和定直線CK的距離相等，所以點P的軌跡是拋物線．

經過反復檢查后我們肯定教師J的解法是正確的，但教師C的證明似乎又是合理的，那么問題到底出在哪里呢？

4 尋根究源，解決問題

第2天，我們接著討論．找到有關圓錐面被平面截得交線方面的書籍，仔細研讀后，終于發現了問題所在.

我們知道，用一個垂直于圓錐的旋轉軸的平面截圓錐，截得的曲線是圓．用不垂直于圓錐的旋轉軸的平面截圓錐，當截面與旋轉軸的夾角不同時，可以得到橢圓、雙曲線、拋物線．教材第42頁的探究與發現中“為什么截口曲線是橢圓”證明了為什么一個平面截圓錐所得曲線是橢圓，但是沒有說明滿足什么條件的平面截得的曲線是橢圓．于是我們開始研究：一個平面以什么樣的角度去截圓錐，可以使所得曲線分別為圓、橢圓、雙曲線、拋物線？

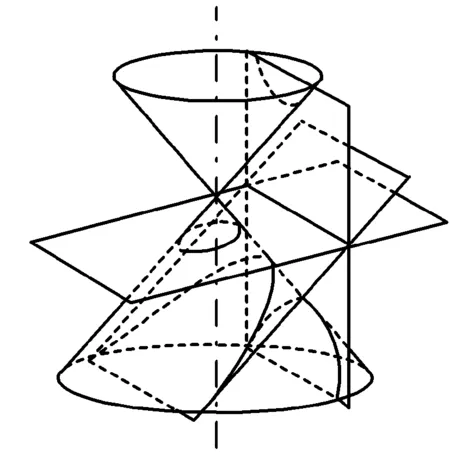
圖3

經過共同努力，我們查證到文獻[1]中記載：拋物線、橢圓和雙曲線統稱為圓錐曲線，因為它們都可以用不經過圓錐頂點的平面去截圓錐面得到．如圖3,設圓錐面的半頂角為α，截面和圓錐面的旋轉軸所夾的角為θ，則

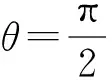
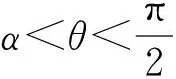
(3)當θ=α時，截得的交線為拋物線；

(4)當0≤θ<α時，截得的交線為雙曲線．

在教師C的證明過程中，雖然截面平行于某一母線，但因為截面α與平面SAO1垂直，所以截面α與圓錐軸的夾角正好等于半頂角，從而截口為拋物線．而問題中的截面與軸的夾角為∠DB1A，顯然小于半頂角∠B1DM，由此可得點P的軌跡確實是雙曲線．

教師X，J起初顯然沒有從截面與旋轉軸的夾角上來考慮，而是從平面與母線是否平行來考慮，他們認為：當截面與軸截面的2條母線相交時，截得的交線為橢圓；當截面與旋轉軸平行時，截得的交線為雙曲線；當截面與旋轉軸垂直時，截得的交線為圓；當截面與母線平行時，截得的交線為拋物線.因為這個結論是從教材的章首圖像中直觀得出的，并沒有作過深入的研究，從而導致了對其認識的片面性．

5 舉一反三，探究規律

為了讓學生能充分掌握這個問題，經共同研究后將上面的問題作了如下變式：

變式1如圖4，已知正方體ABCD-A1B1C1D1，平面ABB1A1內的點P滿足∠PDB1=∠C1DB1，則點P的軌跡是拋物線．

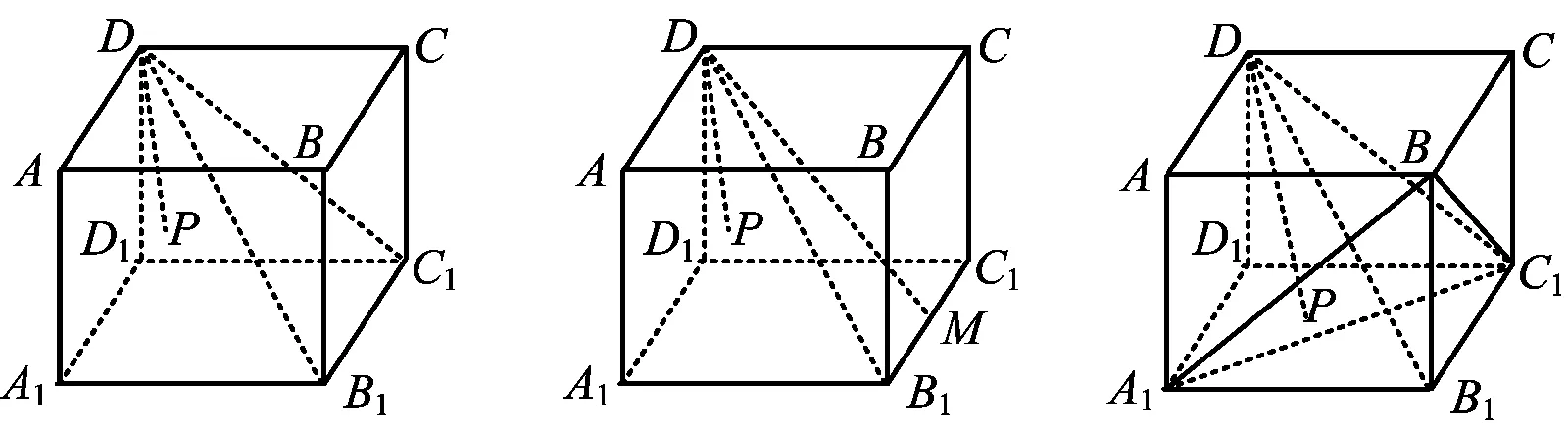
圖4 圖5 圖6

變式2如圖5，已知正方體ABCD-A1B1C1D1，點M是棱B1C1的中點，平面ABB1A1內的點P滿足∠PDB1=∠MDB1，則點P的軌跡是橢圓．

變式3如圖6，已知正方體ABCD-A1B1C1D1，平面A1BC1內的點P滿足∠PDB1=∠C1DB1，則點P的軌跡是圓．

6 反思

新課程改革更加注重提高教師的專業素養，浙江省的教師培訓、學校的校本培訓等等都是通過專家、名師的引領來提高教師的專業素養，為教師提供最新的教育理念、教育信息以及各種操作技能．他們的教學中蘊含著深刻的教育理念、深厚的文化底蘊、高超的駕馭技巧.故向他們學習是我們提高專業素養的途徑之一，但是這樣的學習機會并不多．因為在教學中接觸最多的是同伴，所以同伴互助是提高專業素養的另一途徑．同伴互助作為一種新的教學策略和學習方式，它適用于教師和學生；適用于數學及各個學科的教學和學習．通過同伴交流，解決問題，引起反思，共同分享經驗，進行專業切磋，可以不斷促進教師共同成長．

當然要實現同伴的交流，需要良好的研討氛圍，在教學過程中找到值得探究的問題，如數學問題，課堂的教學問題.提出一個問題就是一個研討的抓手，如教師C提出的問題：“學生熟練掌握了二次函數的平移，而對一次函數的左右平移卻經常出錯.”教師G提出的問題“為什么學生對解題的技巧重視程度大大超過對解題方法的重視程度？”對諸如此類的問題,我們都做過認真的研討，有時找學生，讓學生談談自己的思考過程和想法.有不明白的地方，找書籍、雜志等學習.這樣的討論既可以提高專業水平，也會帶來快樂.

新課改提倡要注重數學知識的實際背景，讓學生體驗知識的產生和發展的過程，教師在備課過程中深入了解概念，明白概念的來龍去脈,學習解決問題的方法，通過交流解決是再好不過的方式.當你把一個思想與他人交流時,有時可以得到2個思想,交流可以讓思想碰撞出火花.同伴互助不僅可以解決問題，也應成為教師的一種生活方式.

參 考 文 獻

[1] 周榮理．截得的交線是怎樣的圓錐曲線[J]．成功(教育),2008(6):55-58.

[2] 左璜,黃甫全．國外同伴互助學習的研究進展與前瞻[J]．外國教育研究,2010(4):53-59.

[3] 徐曼．教師同伴互助的問題及研對策研究[J]．科學咨詢(教育科研),2009:45-47.

[4] 朱蓮蓮．教師專業素養哪里來[J]．福建論壇(社科教育版),2008(3):67-68.