與三角形有關的競賽題分類探究

● (鎮海蛟川書院 浙江寧波 315201)

三角形是最基本的幾何圖形之一，平面幾何中的許多問題往往可歸結于三角形問題進行解決.三角形知識因其基礎性強、起點低、能夠靈活地融入到其他知識中去，一直受到命題者的青睞,因此熟練掌握三角形邊角關系、全等三角形與特殊三角形的性質和判定及應用，對于解決線角的相等、不等以及和差等數量關系，研究平行、垂直等位置關系很有必要.筆者以其在初中競賽中的常見類型進行分類，擬對這類問題的常見解法作一些探討.

1 三角形邊角關系的相關問題

三角形的3條邊相互制約，3個內角之和為定值，邊與角之間有密切的聯系，如三角形三邊關系定理及推論、三角形內角和定理及推論等，大角對大邊、大邊對大角等，它們在線段與角度的計算、圖形的計數等方面有廣泛的應用．

1.1 借助于三角形角的關系解題

例1已知銳角△ABC的3個內角A,B,C滿足：A>B>C，用α表示A-B，B-C以及90°-A中的最小者，則α的最大值為______.

解因為α=min{A-B,B-C,90°-A},所以

α≤A-B,α≤B-C,α≤90°-A,

從而 6α≤ 2(A-B)+(B-C)+3(90°-A)=

270°-(A+B+C)=90°,

于是

α≤15°.

當且僅當A=75°,B=60°,C=45°時滿足題設條件，此時α可取得最大值15°.

評注角是幾何中最活躍的元素，與角相關的知識十分豐富.在三角形中，內角和定理、內外角關系定理、等腰三角形2個底角相等，利用這些獨特的等量關系可以找到角與角之間的“和”、“差”、“倍”、“分”關系.

1.2 借助于三角形三邊關系解題

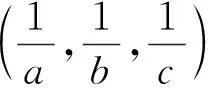
(2012年全國初中數學聯賽試題)

解依題意得

由式(1)得

b>c-a，

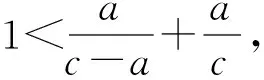
化簡得

a2-3ac+c2<0，

2邊同除以c2，得

從而

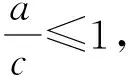
1.3 借助于邊角關系靈活解決綜合問題

例3閱讀下面的情景對話，然后解答問題：

老師：我們新定義一種三角形，2邊平方和等于第3條邊平方的2倍的三角形叫做奇異三角形．

小華：等邊三角形一定是奇異三角形！

(1)根據“奇異三角形”的定義，請你判斷小華提出的命題是真命題還是假命題？

(2)在Rt△ABC中，∠ACB=90°，AB=c，AC=b，BC=a，且b>a.若Rt△ABC是奇異三角形，求a∶b∶c.

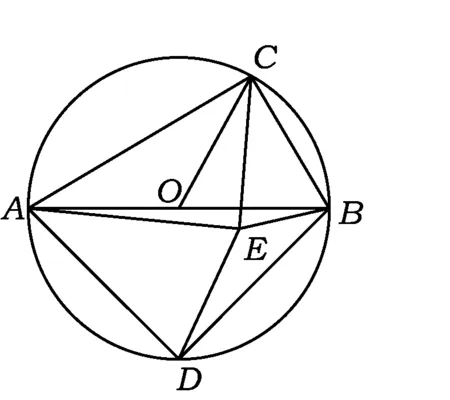
圖1

①求證：△ACE是奇異三角形；

②當△ACE是直角三角形時，求∠AOC的度數．

(2011年浙江省寧波市數學中考試題)

(1)真命題(過程略).

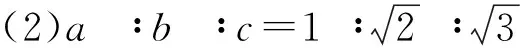
(3)①證明設⊙O的半經為R，因為AB是⊙O的直徑，所以

∠ACB=∠ADB=90°.

從而

又因為AC2+BC2=AB2，BC=CE,所以

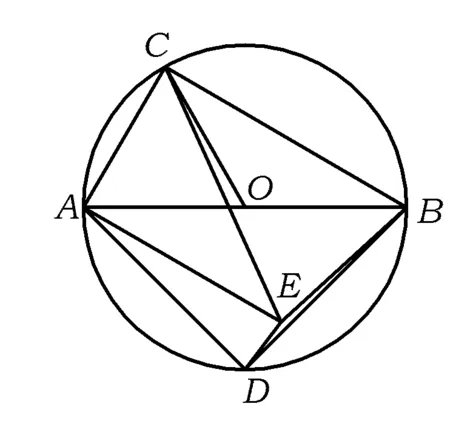
圖2

故△ACE是奇異三角形.

②解如圖2，△ACE是直角三角形.

若∠ACE=90°，則點E與點B重合，即點D與點B重合，不合題意.

若∠AEC=90°，則AE2+CE2=AC2.

當AC2+CE2=2AE2時，AE2=2CE2,從而

即

AB=2BC,

于是

∠BAC=30°，

因此

∠AOC=120°.

當AC2+AE2=2CE2時,CE2=2AE2,從而

即AB=BC，不合題意.

若∠CAE=90°，則AE2+AC2=CE2.

當CE2+AC2=2AE2時,AE2=2AC2,從而

即

AB=2AC，

于是

∠ABC=30°，

因此

∠AOC=60°.

當CE2+AE2=2AC2時,AC2=2AE2,從而

即AC=AB，不合題意.

綜上所述，∠AOC=120°或∠AOC=60°.

評注試題以新定義的“奇異三角形”為背景，成功地跳出勾股定理的局限.新穎活潑的對話情景將等邊三角形、直角三角形、圓等初中數學的核心內容巧妙地融合起來.問題解決從三角形邊和角的關系入口，綜合運用分類、代數的變形和銳角三角函數，起點低、落點高，學生經歷了模仿、辨析、應用3個環節，凸現了問題解決的全過程.

2 三角形“四心”的相關問題

三角形的內心、外心、垂心及重心(以下簡稱“四心”)是新頒發的《初中數學競賽大綱》特別加強的內容，與四心有關的幾何問題涉及知識面廣、難度大、應用的技巧性強、方法靈活，是考查學生邏輯思維能力和創造思維能力的較佳題型.

2.1 借助于垂心的性質解題

例4已知銳角△ABC的頂點A到垂心H的距離等于它的外接圓半徑，則∠A的度數是

( )

A.30° B.45° C.60° D.75°

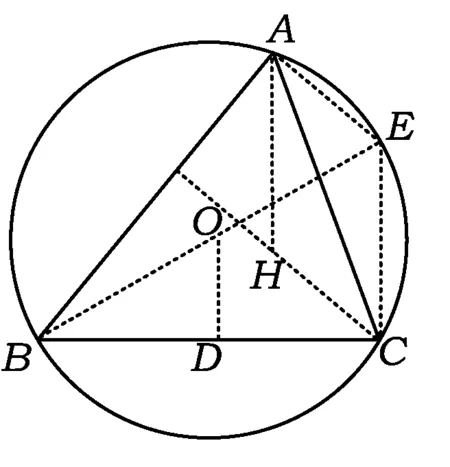
圖3

解如圖3，銳角△ABC的垂心H在三角形的內部，設△ABC的外心為O，D為BC的中點，BO的延長線交⊙O于點E.聯結CE,AE,從而CE∥AH,AE∥CH，則

OB=AH=CE=2OD，

于是 ∠OBD=30°，∠BOD=60°，

因此

∠A=∠BOD=60°.

故選C.

評注三角形3條高線所在直線的交點叫做三角形的垂心.由于垂足位置的不確定性，遇到高線時常用的思想方法是分類討論、構造相似三角形、四點共圓等.

2.2 借助于內心的性質解題

例5在△ABC中，AB=7，BC=8，CA=9，過△ABC的內切圓圓心I作DE∥BC，分別與AB，AC相交于點D，E，則DE的長為______．

(2013年全國初中數學聯賽試題)

解答過程參見本刊2014年第7期第15頁.

評注三角形3條角平分線的交點叫做三角形的內心，即內切圓圓心.由于角平分線的軸對稱性，遇到內心問題時的解法有構造對稱圖形、作高線、面積法等.

2.3 借助于重心性質解題

例6我們知道，三角形的3條中線一定會交于一點，這一點叫做三角形的重心.重心有很多美妙的性質，如有關線段比、面積比就有一些“漂亮”的結論，利用這些性質可以解決三角形中的若干問題.請你利用重心的概念完成如下問題：

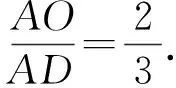
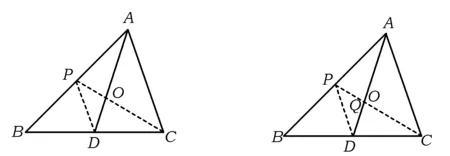
圖4 圖5

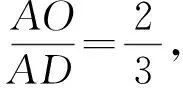
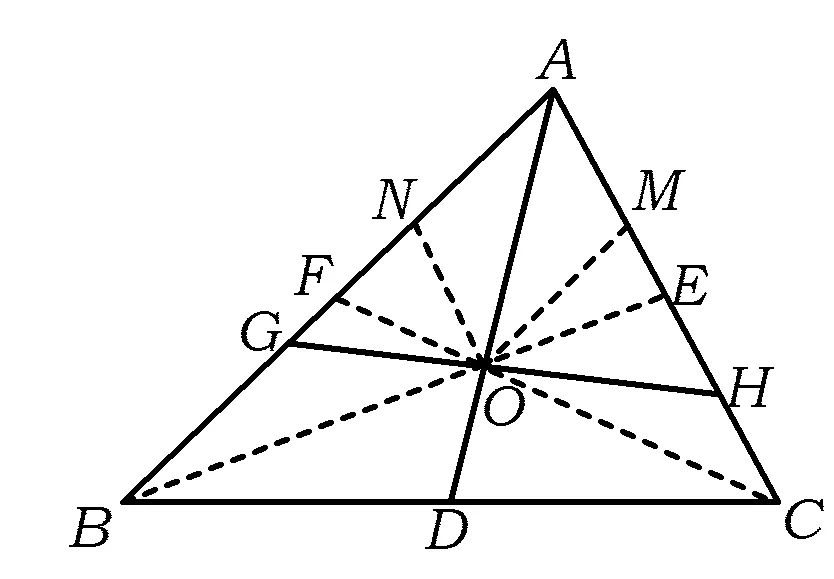
圖6

(2013年四川省綿陽市數學中考試題)

(1)證明由△OPD∽△OCA，得

從而

即

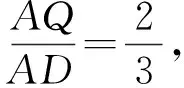
(3)解如圖6，聯結CO并延長交AB于點F，聯結BO并延長交AC于點E，過點O分別作AB,AC的平行線OM,ON，分別與AC,AB交于點M,N.因為點O是△ABC的重心，所以

在△ABE中，由OM∥AB知

即

同理可得

在△AGH中，由OM∥AG知

同理可得

從而

即

亦即

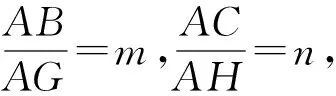
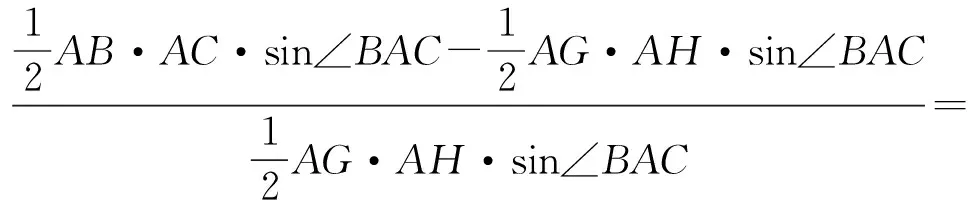
mn-1=(3-n)n-1=-n2+3n-1=

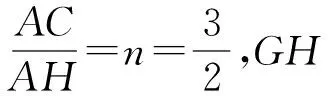
評注三角形3條中線的交點叫三角形的重心.解題時涉及到中線、比例、面積等多種知識，往往入口寬、方法多、綜合能力要求很高，在各類競賽中頻繁出現.

2.4 借助于外心性質解題

例7設△ABC的外心，垂心分別為O,H，若點B,C,H,O共圓，則對于所有的△ABC，求∠BAC所有可能的度數．

解答過程參見本刊2014年第7期第14頁.

評注三角形3條邊的垂直平分線(中垂線)的交點叫三角形的外心.外心問題常與中點、垂直相聯系，由于外心的位置與三角形的形狀有關，因此分類討論是常用的思想方法.本例從外心過渡到重心，很是自然.

3 與三角形面積相關的問題

平面幾何學的產生起源于人們對土地面積的測量，面積是平面幾何中一個重要的概念，聯系著幾何圖形中的重要元素——邊與角，而以三角形為載體的面積問題尤為常見.計算圖形的面積是幾何中一種常見的問題，求三角形面積的基本方法有：直接法、割補法、等積法、等比法等.

3.1 借助于方程模型直接解題

例8如圖7,△ABC的面積是1,AD=DE=EC,BG=GF=FC，求陰影四邊形MNFG的面積.

解(1)先求四邊形FNEC的面積.設S△FNC=x,S△ECN=y,則

S△BNC=3x,S△ANC=3y.

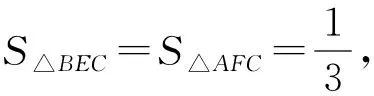
即

故

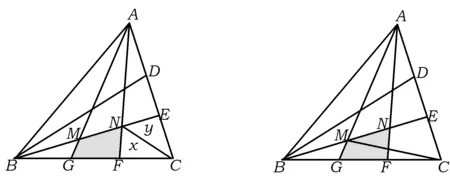
圖7 圖8

(2)再求△BGM的面積.如圖8，聯結MC.設S△BGM=u，S△MEC=v,則

S△CGM=2u，S△MAC=3v,

從而

式(5)×3-式(6)，得

即

故

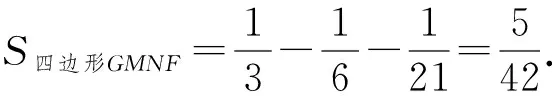
評注通過方程模型解決面積問題是一個銳利武器，一般思路為：設元，在圖形中找等量關系列方程并求解，從而使面積問題迎刃而解.

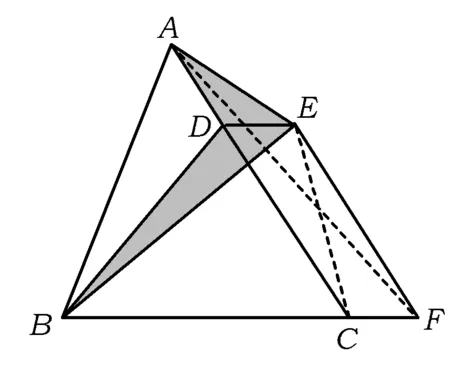
圖9

3.2 借助于等積模型解題

例9如圖9，已知△ABC的面積為24，點D在線段AC上，點F在線段BC的延長線上，且BC=4CF，四邊形DCFE是平行四邊形，則圖9中陰影部分的面積為

( )

A.3 B.4 C.6 D.8

(2013年全國初中數學聯賽試題)

解聯結CE，因為DE//CF，所以S△DEB=S△DEC，因此陰影部分的面積等于△ACE的面積．聯結AF，由EF∥CD，知S△ACE=S△ACF，又因為BC=4CF，所以S△ABC=4S△ACF．故陰影部分的面積為6．

評注常見等積模型：(1)等底等高的2個三角形面積相等；(2)2個三角形高相等，面積比等于它們的底之比，2個三角形底相等，面積比等于它們的高之比；(3)夾在一組平行線之間的等積變形，如圖10，若AB∥CD,則S△ACD=S△BCD，反之，若S△ACD=S△BCD，則AB∥CD．在利用等積模型時，如何選擇“中間橋梁”是關鍵.

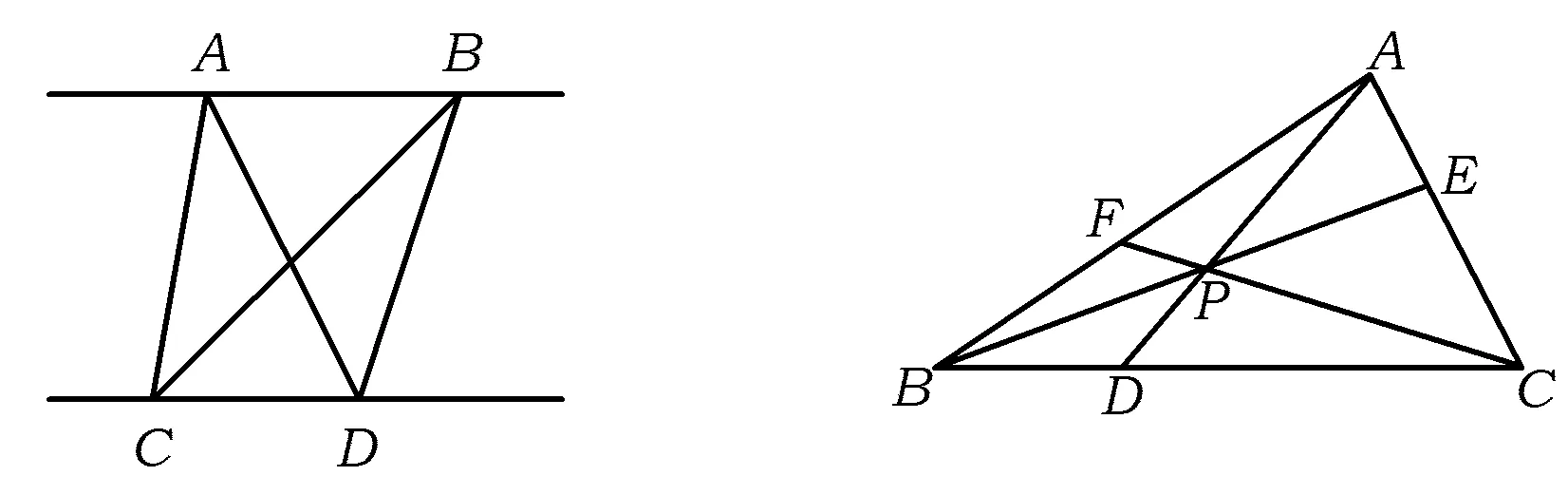
圖10 圖11

3.3 借助于等比定理解題

例10如圖11，P是△ABC內一點，BP，CP，AP的延長線分別與AC，AB，BC交于點E，F，D.考慮下列3個等式：

其中正確的有

( )

A．0個 B．1個 C．2個 D．3個

解(1)正確，理由：

(2)正確，理由：

(3)正確，理由：

故選D.

評注此例極為經典，囊括了燕尾定理、梅涅勞斯(Menelaus)定理(簡稱梅氏定理)等的探究過程，因涉及到的等比定理等知識均屬于初中數學的難點，適當拓展，很是有趣.

4 構造圖形解決三角形綜合性問題

4.1 構造全等三角形解題

例11如圖12，在△ABC中，∠B=90°，M為AB上一點，使得AM=BC，N為BC上一點，使得CN=BM，聯結AN,CM交于點P.試求∠APM的度數，并寫出推理證明的過程.

(2008年全國初中數學聯賽

天津賽區試題)

證明過點M作AB的垂線MD，使MD=CN，聯結DA,DN，則四邊形MDNC是平行四邊形，從而△DMA≌△MBC，于是DA=MC，而MC=DN，故DN=DA.因為∠ADN=90°，所以∠AND=45°，利用MC∥DN，得∠APM=∠AND=45°.

評注當現有圖形的任何2個三角形之間不存在全等關系時，則需要添置輔助線，構造全等三角形來研究平面圖形的性質.常見策略有：已知角平分線，可利用軸對稱構造全等三角形；已知中點，可利用中心對稱性構造全等三角形；已知特殊角度，可旋轉特殊角度構造全等三角形.

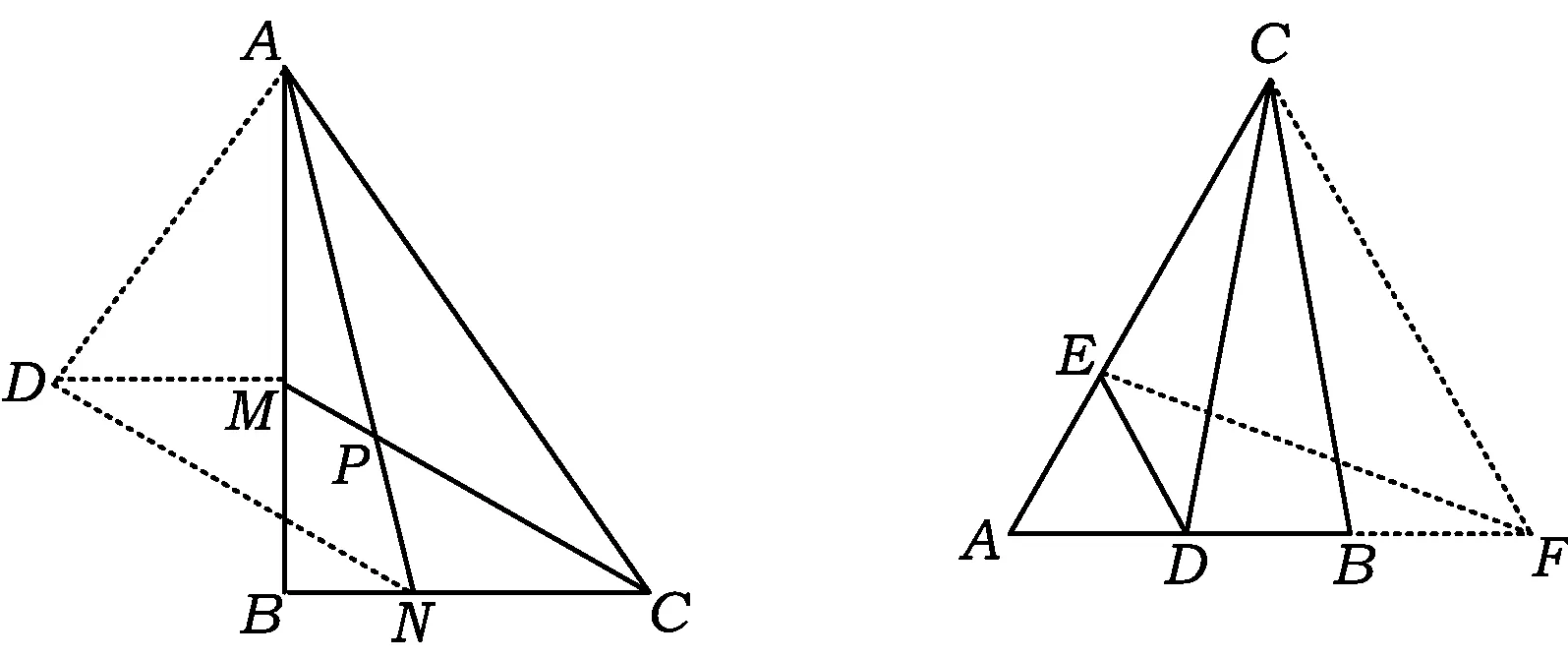
圖12 圖13

4.2 構造對稱圖形解題

例12在△ABC中，已知∠CAB=60°，D，E分別是邊AB，AC上的點，且∠AED=60°，ED+DB=CE，∠CDB=2∠CDE,則∠DCB=

( )

A．15° B．20° C．25° D．30°

(2010年全國初中數學聯賽試題)

解如圖13，延長AB到點F，使BF=ED，聯結CF，EF．因為∠EAB=∠AED=60°，所以

∠EDA=60°,∠EDB=∠CED=120°.

由AD=AE=ED=BF,知

CE=ED+DB=DB+BF=DF，

于是

AC=AF，∠ACF=∠AFC=60°.

又因為∠EDB=120°，∠CDB=2∠CDE，所以

∠CDE=40°,∠CDB=80°,

∠ECD=180°-∠CED-∠EDC=20°.

在△CDA和△CBF中，

CA=CF，∠CAD=∠CFB=60°，AD=BF，

從而

△CDA≌△CBF，

于是

∠FCB=∠ACD=20°．

故

∠DCB=60°-∠CDE-∠FCB=20°．

評注當證明相等的2條線段或2個角所在的三角形全等的條件不充分時，則需根據圖形的軸對稱性或其他對稱性質，先證明別的2個三角形全等以補足條件.

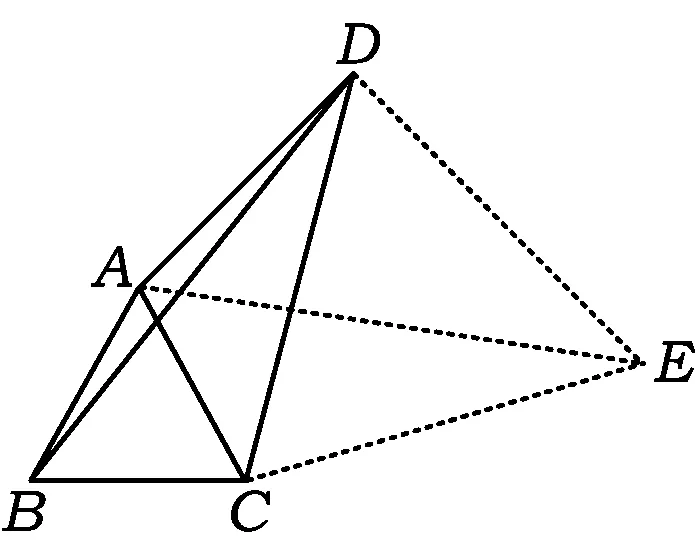
圖14

4.3 構造等邊三角形解題

例12如圖14，在四邊形ABCD中，AC，BD是對角線，△ABC是等邊三角形．∠ADC=30°，AD=3，BD=5，則CD的長為

( )．

(2012年全國初中數學聯賽試題)

解如圖14，以CD為邊作等邊△CDE，聯結AE，可得△BCD≌△ACE，從而BD=AE.因為∠ADC=30°，所以∠ADE=90°.在Rt△ADE中，AE=5,AD=3,故

所以

CD=DE=4.

評注對于某些幾何題，尤其是條件中出現或隱含著60°或120°的幾何題，利用構造等邊三角形的方法，可找到簡捷的解題途徑.

與三角形有關的競賽題類型多、難度大、思維要求高，但只要我們夯實基礎，拓寬思路，關注知識間的縱橫聯系，熟練運用分類討論、數形結合及轉化、化歸等思想和方法，必能有章可循.