浙江省近6年高考數學試題的深度解讀與展望

● (余杭高級中學 浙江杭州 311100)

在浙江、山東、廣東、江蘇、貴州等多地市就高考備考、課堂教學、教師專業發展等方面作學術講座、觀摩課幾十場次，在浙江電視臺教學相關欄目做2010年高考考前指導.主編(編審)《優化方案》、《三維設計》、《世紀金榜》等高三復習用書多本(部)，為多家雜志、報紙、一些地市的模擬考試編寫試題上百套，兼任多家報紙、雜志的特約撰稿、特約編審等.

2009年浙江省開始新課程下的高考，6年時間如白駒過隙，2015年起新一輪高考即將拉開帷幕，回顧近6年浙江省數學高考試題，相信對認識高考，特別是認識浙江特色的高考，搞好以后的數學教與學將大有裨益.

1 近6年高考數學試題解讀

1.1 穩中漸變，貼近學生實際

浙江省數學高考試題堅持“考查基礎知識的同時，注重考查能力”，充分體現“以能力立意”的指導思想，符合《考試說明》的各項要求，適合浙江省考生的實際水平，保持了命題的連續性、穩定性和創新性.

1.1.1 題型結構

從2007年始，浙江省數學高考試題在題型上一直保持“10+7+5”的形式，其中，解答題一般是一道題2個小題(以理科試題為例，只有2012年和2014年略有微調，其中，2012年第22題第(1)小題和2014年第19題第(2)小題都包含2個小題)，難度梯度遞進.經過實踐證明題量是合適的，題型搭配比較合理，選擇題、填空題照顧知識覆蓋，解題靈活，解答題深度考查、全面檢測綜合素質與能力.

1.1.2 難度結構

試題總體難度相對穩定，從表1可以看到，試題難度基本上穩定在0.6左右，理論上，大型選拔性考試難度在0.55左右會有較好的區分度，但是，考慮到現在的招生規模、學生減負、社會現實等因素，0.6左右是各方面都可以接受的一個難度水平；理科試卷的難度相對文科要大，這是文科、理科數學教學的現狀以及繼續學習的現實需要決定的.試題難度構成上大致按照3∶5∶2的比例，個別年份有些波動，一般在下一年會加以調整，如2009年理科試卷中容易題比例偏大(50%)，中檔題、難題比例偏低，在2010年的試卷中明顯得以調整.在試卷基本穩定的基礎上，上一年的統計數據也往往是下一年試卷難度調整的風向標.

整張試卷按照選擇題、填空題、解答題呈現3個難度層次，在每種題型內又各有難度臺階，整張試卷呈現“分題把關”模式，一般在選擇題的第9，10題，試題難度會提升一個層次；填空題第16，17題，有一部分考生會感覺比較難上手，特別是第17題；解答題最后2個題目基本在一個“難度平臺”上，共同起到“壓軸題”的作用.

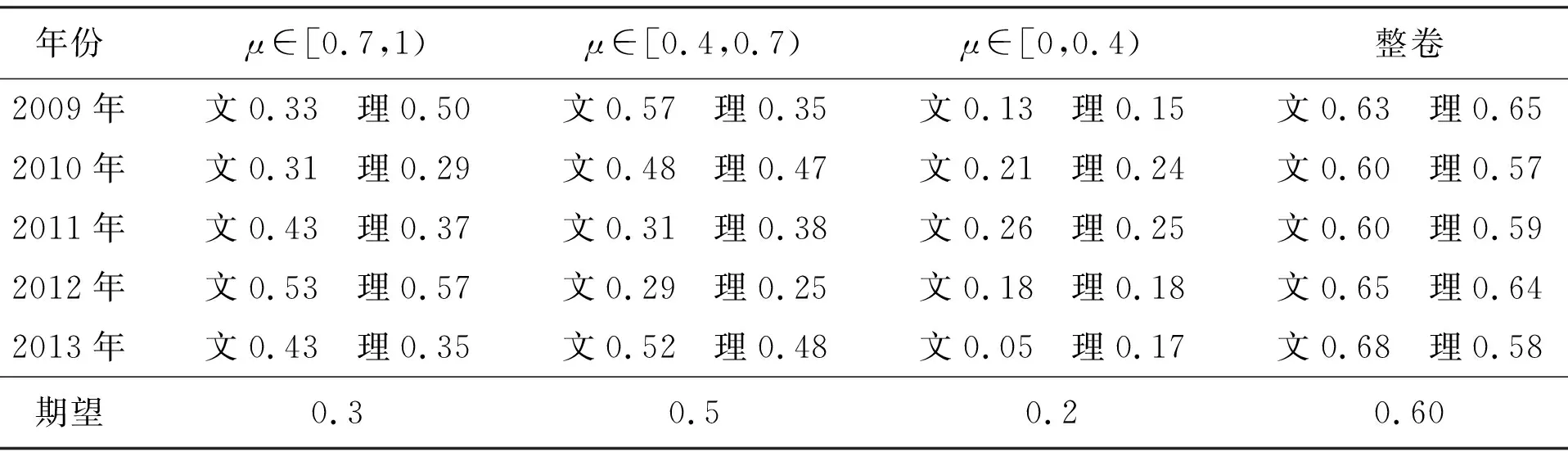
表1 2009～2013年浙江省數學高考試卷難度情況統計一覽表

表1中μ表示試題所占分數百分比.

1.2 全面考查，凸顯主干知識

從表2(為節省版面，此處只列出理科卷的考查內容分布)中可以看出，近幾年的高考試卷在《考試說明》要求的各個模塊上基本都有試題，具有較廣的覆蓋率，如復數、算法初步等內容每年都會有1道試題，體現出“學什么考什么”的導向；同時，對支撐高中數學的重點內容突出考查，凸顯主干知識，為考生將來的發展奠定良好的學科基礎，如理科的函數與導數、三角函數與解三角形、立體幾何、解析幾何、概率等.文科中數列代替理科的概率內容占有較大比重.

表2 2009～2014年浙江省數學高考理科卷考查內容分布

1.3 立足課本，倡導通性通法

( )

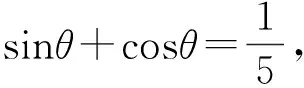
(2007年浙江省數學高考試題)

( )

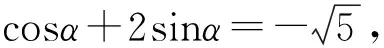
(2008年浙江省數學高考試題)

( )

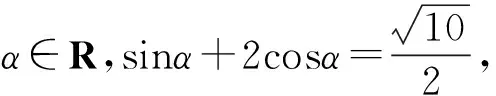
(2013年浙江省數學高考試題)

分析首先本案例是現行人教A版《必修4》第147頁復習題B組第8題的變式，“題在書外，根在書中”，顯示出高考命題規避復習資料、規避題型的命題導向，引導中學數學教學更好地利用課本，在“減負增效”上下功夫，減輕學生的負擔.同時，立足通性通法是浙江省數學高考命題一直延續的特點，引導“題不在多，理解則靈”，體現反對題海戰術的意圖.本案例都可以求解的方法有回歸定義、“齊次化”、等差代換、合一變形等，這些都是解決此類問題的“通法”.其中第2題還可以利用求導簡潔求解，顯示了“特技”的效果.造成這種區別的原因是“形同質異”，對于acosα+bsinα=c下求值，當a2+b2=c2時,“特技”就一定能使用，也就是說“特技”是一定條件下的“通法”，是問題“通性”下“個性”的充分挖掘、利用，是對問題本質的把握.所謂“通法”與“特技”是相對的，“通法”與“特技”不存在“鴻溝”，只是使用條件的差異、認識問題的程度不同.

1.4 體現方法，全面檢測能力

數學思想方法屬于數學知識范圍，是程序性知識，是“怎么做”的問題，較之事實性、概念性知識有更高的層次.數學思想方法的掌握情況既是數學知識素養的體現，又是能力強弱的表現之一，是中國數學教育特色之一.浙江省數學高考試題呈現以基礎為抓手，以思想方法為依托，全面考查數學能力的命題格調，命題手段不斷改進，體現出鮮明的浙江特色.主要考查的數學思想方法有函數與方程思想、數形結合思想、分類與整合思想、化歸與轉化思想等，這里選取2012年數學高考理科試題為例加以分析.

案例2設a∈R，若x>0時，均有[(a-1)x-1](x2-ax-1)≥0，則a=______．

(2012年浙江省數學高考理科試題第17題)

圖1

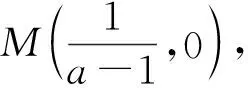
表3 2012年浙江省數學高考理科試題對數學思想方法考查的量化分析

由表3可以看出：(1)按出現頻數從高到低依次是化歸與轉化思想、函數與方程思想、數形結合思想、分類與整合思想等.(2)高考對數學思想方法的考查貫穿全卷.客觀題注重考查基礎知識、基本技能，同時又著眼于數學思想方法的考查;解答題在對數學思想方法考查的廣度與深度上都比客觀題更加突出.不同題型、不同位置的試題在考查思想方法類型與層次上明顯有層次、有梯度.(3)數學思想方法的考查以基礎知識為依托、以能力考查為目的.思想方法的考查和基礎知識的考查相結合，以思想方法指導知識的運用，解題的思路在思想方法的指引下明晰、完整，解題的過程在思想方法的引導下優化、流暢，或者簡化運算，或者明晰思路，或者化難為易、化繁為簡，使問題得到更快、更簡潔、更優美的解決.基礎題靠知識，中檔題靠思想，難題靠能力，數學思想方法掌握情況可以反映出考生對數學的理解程度，體現考生的能力層次.

1.5 關注本質，考查深度理解

數學本質是數學的基本問題，是高考數學命題的出發點之一.一般意義上，數學本質包含數學基本概念、數學思想方法、數學特有的理性思維方法以及數學美、數學精神等.浙江省自主命題一直關注數學本質的考查，不少試題注重從一個小問題出發，力求說明一個大觀點，體現一個大意境，引導中學數學教學關注數學本質的理解.

案例3已知e為自然對數的底數，設函數f(x)=(ex-1)(x-1)k(其中k=1,2)，則

( )

A．當k=1時，f(x)在x=1處取到極小值 B．當k=1時，f(x)在x=1處取到極大值

C．當k=2時，f(x)在x=1處取到極小值 D．當k=2時，f(x)在x=1處取到極大值

(2013年浙江省數學高考理科試題第6題)

分析數學是由概念、命題組成的邏輯系統，數學概念是現實世界中空間形式和數量關系及其屬性在思維中的反映，是數學地認識事物的思想精華，它蘊含了豐富的創新素材，是數學抽象性的基礎，是構建數學大廈的奠基石.正確理解數學概念是掌握基礎知識的前提，是學好定理、公式和掌握數學方法、提高解題能力的基礎.考題年年新，概念是其根，變的是形式，不變的一定有對概念的考查.

本題考查函數極值、極值點、零點的概念以及指數、一次、二次函數的性質，函數在某點取得極值的必要條件和充分條件，意在考查考生對概念的理解、函數方程思想、數形結合思想以及靈活運用知識的能力.當k=1時，f(x)=(ex-1)(x-1)，明顯地，x=1是函數f(x)的一個零點，當01時，f(x)>0，根據極值的概念，x=1處取不到極值，排除選項A,B；當k=2時，f(x)=(ex-1)(x-1)2的一個零點是x=1，當01時，都有f(x)>0，由極小值概念知在x=1處取到極小值.故選C.

涉及極值的問題，有些學生習慣性地利用導數運算，心中只有“數”，目中不見“形”，盲目運算的根源在于沒有概念指引，不能利用概念解題，其結果就是舍本逐末、事倍功半.掌握一個數學概念,不僅意味著文字、符號的記憶，更要理解概念的內涵、外延，理解概念發生、發展的過程，要把握它的數量特征,又要把握它的幾何特征,“豐滿的”概念才能優化解題思路,保證解題正確、快速.

1.6 關注差異，體現人文關懷

根據文、理科學生的實際學習水平，以及進一步學習、發展的需求，文、理科數學考試一直存在著差異.如解答題通常：“姊妹題”選材，難度差異也很大，相同試題的素材主要集中在思維層次較低的知識上，如集合運算、復數運算、三視圖、程序框圖；不同題，一方面是取自知識要求差異部分，比如理科的排列組合、二項式定理、隨機變量及其分布、空間向量與立體幾何等，另一方面是在相同知識載體上，設計不同思維層次、不同能力要求的試題，如圓錐曲線、函數與導數等.

2 2015年高考展望

2.1 穩定、創新是常態

從2004年浙江省開始自主命題，命題思路、指導思想、命題技術至今都已相當成熟，2015年的高考將遵循《(2012版)浙江省普通高中學科指導意見(數學)》的各項規定，依照《考試說明》實現平穩過渡，當然，有更多地創新值得期待，如壓軸題的命制，自選模塊中導數、概率等內容的重新定位與命制等.

2.2 調整各板塊分數，更加突出主干知識

各知識板塊所占分數是大家高度關注的問題之一.高考在各個知識板塊的分數分配有一個基本原則，就是該知識板塊所占的課時百分比，然后在合理的范圍內加以調整.根據2012版《浙江省普通高中學科教學指導意見》，相對2009～2014年的高考，各個知識板塊所占課時比都有較大變化，詳見表4、表5(※為選考或者選學不進入高考內容).

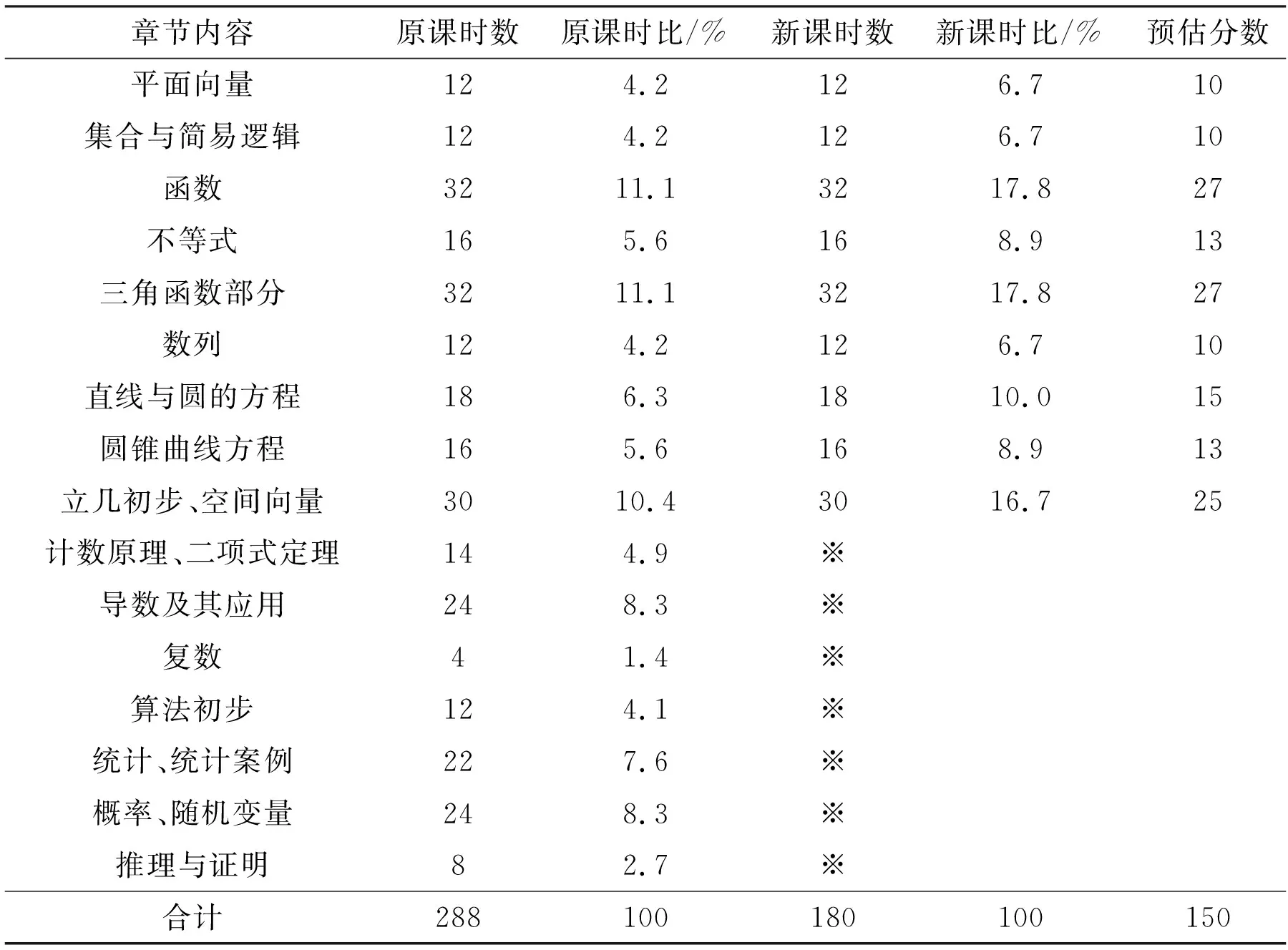
表4 2015年高考各知識板塊課時數、課時比情況對照(理科)

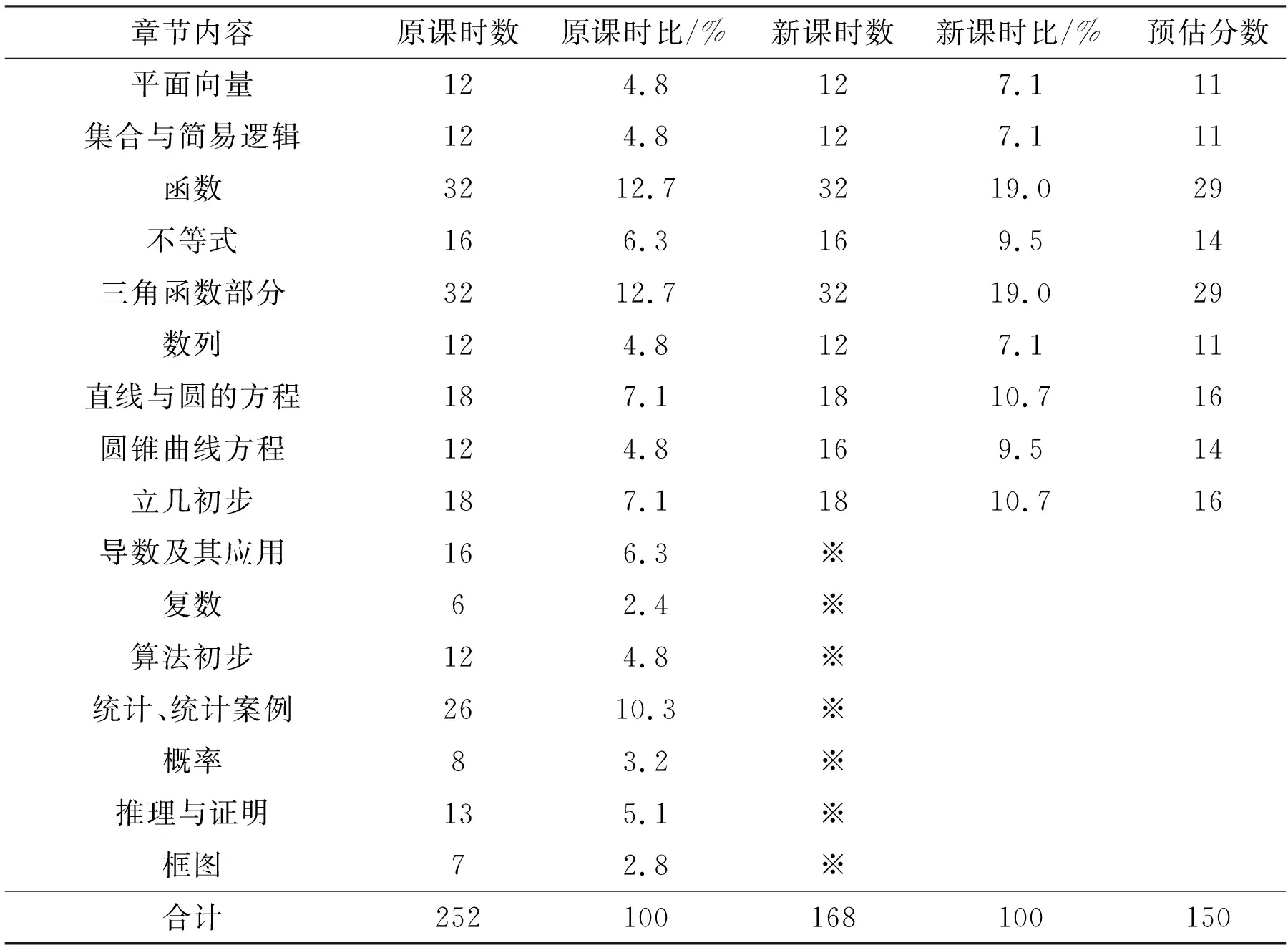
表5 2015年高考各知識板塊課時數、課時比情況對照(文科)

可以看出，調整后的考試內容更加集中，主干知識的考查會更加突出，如理科的函數、立體幾何、解析幾何(直線與圓、圓錐曲線)、三角函數部分，分數都應該在25分以上，再考慮到這些內容與其他知識的綜合，這些內容的掌握情況在很大程度上會決定數學學科的考試情況；而文科由于課時相對更少，函數、解析幾何(直線與圓、圓錐曲線)、三角函數部分的分數都可能會接近30分，立體幾何約占16分，掌握主干知識的重要性更加顯而易見.相信新的高考試題依然堅持“全面考查”的特色，主干知識考查的地位更加顯著.由于導數內容的退出，涉及函數部分的考查會更加強調函數的本質，在考查的形式及難度把握上相信會遵循考試說明要求，作為命題研究的一個重中之重，體現出新的特點.

2.3 淡化特殊技巧，提倡通性通法

在社會一直關注“減負”的大背景以及中學數學教學目標的指引下，高考肯定會更加注重“通性通法”，引導扎實基礎、熟練通法，充分發揮課本的效能，不出偏、難、怪的試題，引導規避“題海”、“題型”，給考生營造公平的競爭情境.

2.4 更加注重對數學本質的考查，體現思想方法的重要性，突出能力考查

近幾年的數學高考試題以基礎知識、基本技能的考查為載體，體現對數學思想方法的考查，體現能力立意，重在對數學本質的理解，反“題海”、反“套路”，為考生提供公平情境是浙江卷一貫的風格；試題具有較高的信度，既能有效考查學生的數學能力、心理品質，也能對數學教學產生正確的導向．倡導數學理解，倡導教與學的方式改進，對中學數學教學起到了很好的引導作用.教“題型”、授“套路”，可以“短、平、快”，在平時應試中也可能屢試不爽，不過在規避題型的高考中就會“失效”.

2.5 注重試題的切合性、科學性

高考數學試卷穩中求變是常態，試題變中求新理所當然，只有新才能更好地發揮選拔作用.不過，試題在求新的同時，也會更加注意到考生的現實可能.在2014年的試卷中有諸如以上特點的試題達6～7題，對學生的閱讀理解、運算求解勢必帶來極大障礙，影響不少考生的正常發揮；另如在2013年高考試題中出現的關于“線段”的爭議，在以后的命題中相信也會很好的規避.

2.6 增加應用性考查

2014年填空題最后一題出現了一道“準應用題”，追溯上一次考查應用題還是在2009年的填空題(峰谷電(分段函數)問題)，隨著課程改革的逐步深入，考查方式的靈活多變，必修內容知識點的減少，引導學生學會發現問題、提出問題并應用數學知識解決問題，應用題的考查也勢在必行.

參 考 文 獻

[1] 教育部考試中心.高考數學測量理論與實踐[M].北京：高等教育出版社，2005.2.

[2] 浙江省高考命題咨詢委員會.2009浙江省高考命題解析(理(文)科數學)[M].杭州：浙江攝影出版社，2009.12.

[3] 浙江省高考命題咨詢委員會.2010浙江省高考命題解析(理(文)科數學)[M].杭州：浙江攝影出版社，2010.12.

[4] 浙江省高考命題咨詢委員會.2011浙江省高考命題解析(理(文)科數學)[M].杭州：浙江攝影出版社，2011.12.

[5] 浙江省高考命題咨詢委員會.2012浙江省高考命題解析(理(文)科數學)[M].杭州：浙江攝影出版社，2012.12.

[6] “浙江省高考命題解析”叢書編委會.2013浙江省高考命題解析(理(文)科數學)[M].杭州：浙江攝影出版社，2014.1.

[7] 中華人民共和國教育部制訂.普通高中數學課程標準(實驗)[M].北京：人民教育出版社，2003.4.

[8] 浙江省基礎教育課程改革專業指導委員會.浙江省普通高中學科教學指導意見：數學，2012版[M].杭州：浙江教育出版社，2012.8.