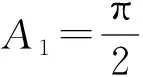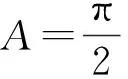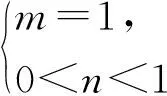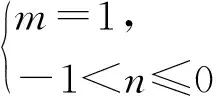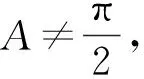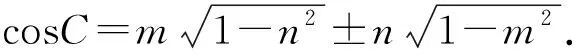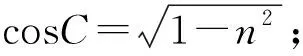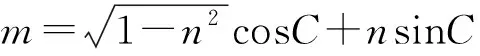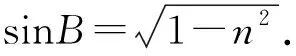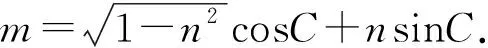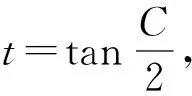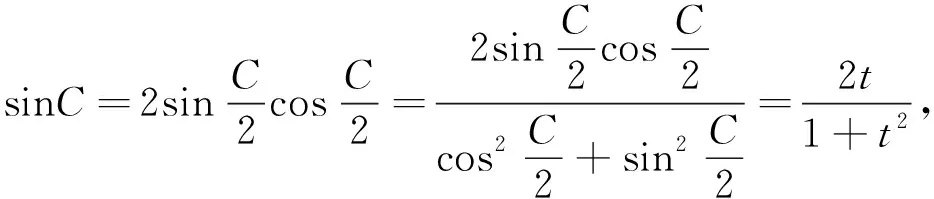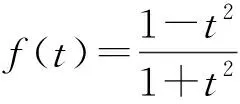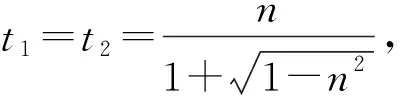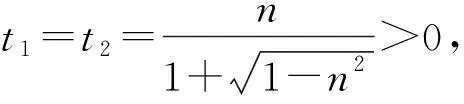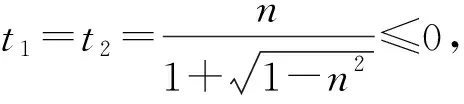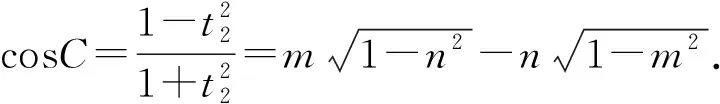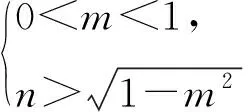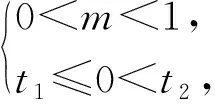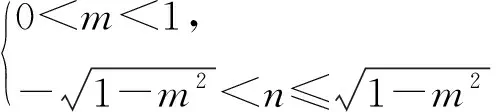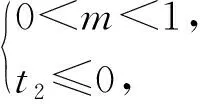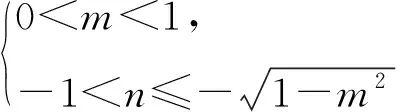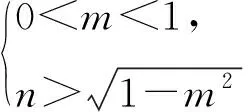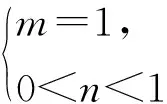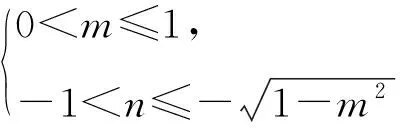由特殊到一般的探究
● (陜西師范大學數學與信息科學學院 陜西西安 710062)
本文呈現一類三角求值問題的推廣探究過程,除體現特殊與一般的數學思想外,還滲透有數形結合、分類討論、函數與方程等多種數學思想,是進行數學思想方法教學的一個良好載體.
1 特殊問題的解決
有一類熟知的三角求值問題:已知三角形中2個內角的函數值,求第3個內角的函數值.如
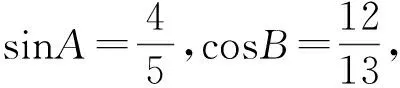
分析先弄清題目的條件和結論,然后溝通條件與結論的聯系,得出解法.
(1)題目有3個條件:
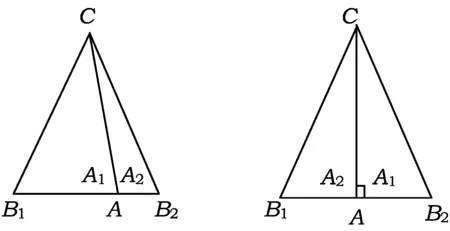
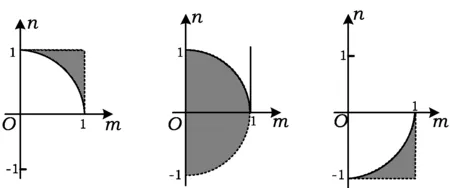
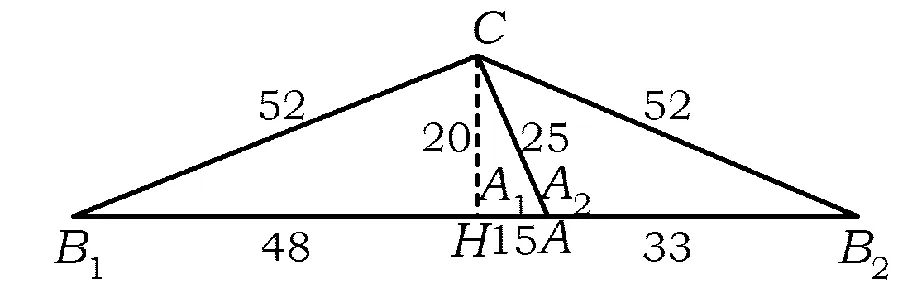
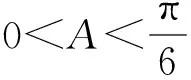
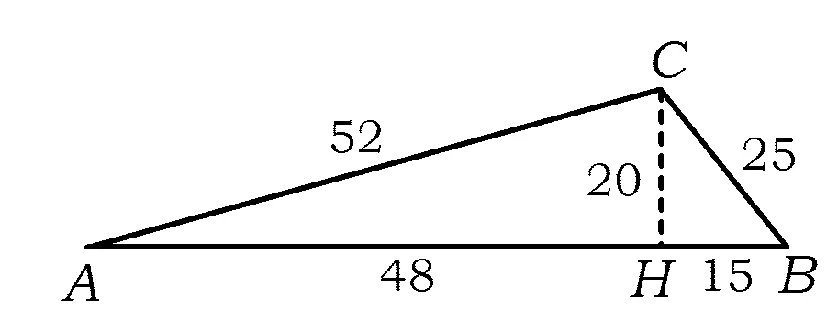
條件1在△ABC中.由此可知0 (2)題目的結論是求cosC的值. (3)溝通題目的條件與結論的聯系.由cosC=cos[π-(A+B)]=-cos(A+B),得 cosC=sinAsinB-cosAcosB.(1) 可見,只需由sinA,cosB求出cosA,sinB,便可求出cosC的值.給出以下2種解法: 從而 sinA=sin[π-(B+C)]=sin(B+C)=sinBcosC+cosBsinC, (2) 將式(2)移項,2邊平方,整理得關于cosC的二次方程 解得 圖1 說明如圖1所示,cosC的2個解分別可在△AB1C,△AB2C中求得,由余弦定理可驗證其正確. sinA=sin[π-(B+C)]=sin(B+C)=sinBcosC+cosBsinC, (3) 圖2 說明如圖2所示,例2也可以在△ABC中用余弦定理求解,在此不再贅述. 從上述求解過程可以看到,由sinA到cosA有2個可能的取值,但這2個值能不能都取到還需要進一步討論.更一般地,當sinA=m,cosB=n時,cosC是不是有解?有幾個解?具體數值是什么?就更加需要抽象的討論了,這是一個很有探究價值的問題. 例3在△ABC中,sinA=m,cosB=n(0 下面給出的2種思路都是數形結合并分類討論,但思路1重在幾何,思路2重在代數. 思路1數形結合討論已知條件中的角. (1)思路分析. 關鍵點1確定cosA. 由于A為三角形的內角,對每一個m∈(0,1],有m=sinA=sin(π-A),故內角A最多有2個取值,記為A1,A2(如圖3,其中B1=B2),滿足 關鍵點2保證A,B能在同一個三角形內. 由A+B+C=π知,A,B在同一個三角形內的充要條件是0 下面只需討論A1+B,A2+B與π(平角)的關系,便可確定Ai(其中i=1,2)與B是否在同一個三角形內,以及有幾個Ai(其中i=1,2)與B在同一個三角形內. (2)討論A1=A2的情況. 圖3 圖4 (3)討論A1≠A2的情況. 情況3若A2+B<π,則0 情況4若0 情況5若π≤A1+B,則π≤A1+B (4)相關結論. 分別把情況1和情況4合并,把情況2和情況5合并,可得: 結論3當A1 思路2代數方法討論二次方程中的正根. (1)思路分析. 第1步:構造一個二次方程,求出它的2個實根. sinA=sin[π-(B+C)]=sin(B+C)=sinBcosC+cosBsinC, (4) (5) 把式(5),式(6)代入式(4),得關于t的二次方程 (7) (8) 所以方程(7)恒有實根(包括等根),解得 (9) 其中t1≤t2.接下來只需討論t1,t2有無正根,正根能取到幾個,并把正根代入式(5)便可求出cosC. 第2步:對t1,t2取正值的情況分類討論. 基本思路是對二次方程(7)中t1,t2的表達式作二級分類:先把t1,t2分為相等的根和不等的根,然后再分為正根與非正根,結合題目所給的m,n(可以先討論m后討論n)進行討論,其邏輯結構如下: (2)討論t1=t2的情況. (3)討論t1≠t2的情況. 若t1≠t2,則由式(8)或式(9)知m≠1,得0 這時,方程(7)只有1個正根t2>0,對應方程(4)的cosC只有1個解.把式(9)代入式(5)可求得 (4)相關結論. 分別把情況1和情況4合并,把情況2和情況5合并,可得: 圖5 圖6 圖7 如果把已知條件{(m,n)|0 由上面的一般性結論,還可以編擬出各種題目用于不同的場合(略).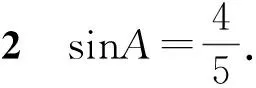
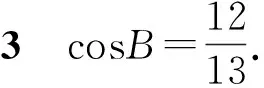
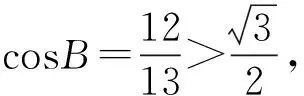
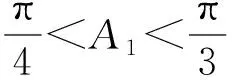
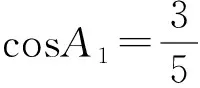
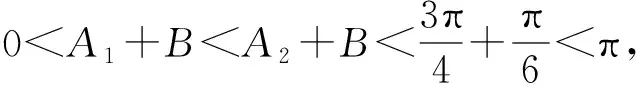
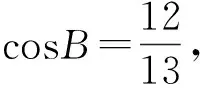
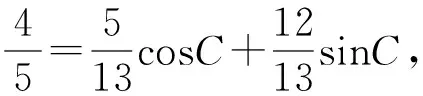
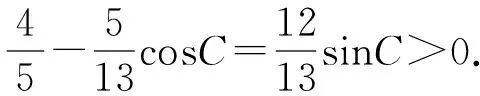
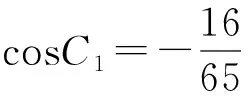
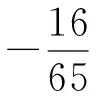
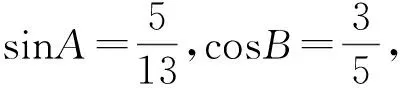
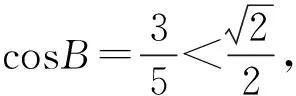
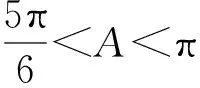
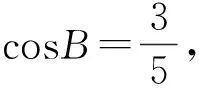
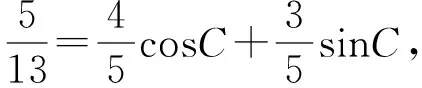
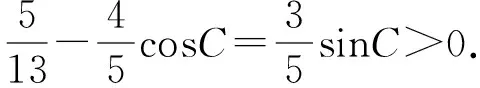
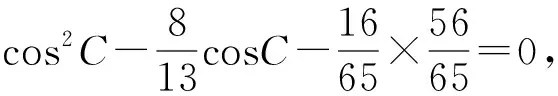
2 一般情況的探究