建構主義理論指導下的初中幾何圖形變換模型教學策略研究

孫丹

摘 要：數學建模是一種主動建構的過程，體現了創造性，數學建模能力就是創新能力的具體體現。因此本文以建構主義理論為指導，探究幾何圖形變換模型教學的有效策略。

關鍵詞：建構主義；幾何圖形；策略

一、建構主義基本理論

建構主義理論提倡在教師指導下的以學習者為中心的學習，教師是意義建構的幫助者、促進者，而不是知識的傳授者與灌輸者。

二、幾何圖形變換的教學策略分析

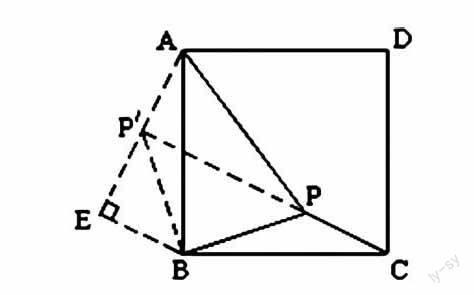
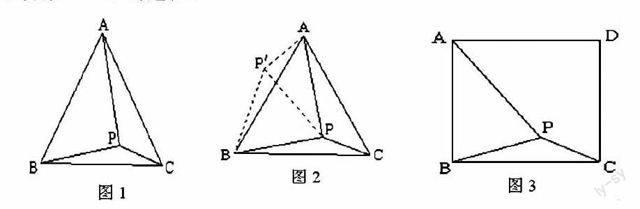
【例1】（閱讀理解式的幾何模型問題），如圖1，在等邊三角形ABC內有一點P，且PA=2，PB=3，PC=1.求∠BPC度數的大小和等邊三角形ABC的邊長.甲同學的思路是：將△BPC繞點B順時針旋轉60°，畫出旋轉后的圖形（如圖2）然后求解。如圖3，在正方形ABCD內有一點P，且PA=5，BP=2，PC=1.求∠BPC度數的大小和正方形ABCD的邊長。

學生在遇到這樣的問題時，通常學生會認為無從下手，但是這時教師首先要樹立學生的自信心，從題目所給材料出發，尋找建立模型的突破口。材料中小明的做法是通過圖形的旋轉來解決問題的，關鍵是旋轉的角度是60度，此時教師要重點向學生提出質疑：為什么旋轉的是60度？如果旋轉的是30度、45度又會如何？引導學生主動發現旋轉60度的玄機就是：題目中原來大圖形是等邊三角形，需要用60度去構造另一個等邊三角形。此時，教師注意引導學生觀察所求的問題中原圖形是有什么特征的圖形，旋轉角度定為多少才更合適？學生自己觀察會發現，所求題目中原圖是一個正方形，這樣只有旋轉90度才能成功構造一個直角三角形，從而解決問題。……