探究性學(xué)習(xí)要關(guān)注數(shù)學(xué)思考和數(shù)學(xué)思想方法

林李嬌

中圖分類號：G622 文獻標識碼：A 文章編號：1002-7661（2014）04-0040-01

數(shù)學(xué)思考，是指在數(shù)學(xué)活動中的思考。我們可以從狹義和廣義來理解：從狹義角度是指學(xué)生關(guān)于數(shù)學(xué)對象的理性認識過程。從廣義角度理解還包括應(yīng)用數(shù)學(xué)解決各種實際問題的數(shù)學(xué)式思考。

曾在2001年7月，教育部頒布的《全日制義務(wù)教育數(shù)學(xué)課程標準（實驗稿）》就在第二部分課程目標中明確提出了“數(shù)學(xué)思考”。這一目標可以說，是作為“促進學(xué)生的終身可持續(xù)發(fā)展是義務(wù)教育的基本任務(wù)”的一個集中體現(xiàn)。

《2011年版數(shù)學(xué)課程標準》作為課程總目標之一的“數(shù)學(xué)思考”是這樣描述的：

1.建立數(shù)感、符號意識和空間觀念，初步形成幾何直觀和運算能力，發(fā)展形象思維與抽象思維。

2.體會統(tǒng)計方法的意義，發(fā)展數(shù)據(jù)分析觀念，感受隨機現(xiàn)象。

3.在參與觀察、實驗、猜想、證明、綜合實踐等數(shù)學(xué)活動中，發(fā)展合情推理和演繹推理能力，清晰地表達自己的想法。

4.學(xué)會獨立思考，體會數(shù)學(xué)的基本思想和思維方式。

新課程對學(xué)生的綜合能力要求之一是：對問題進行思考、抽象概括、模型轉(zhuǎn)換。就是把實際的問題與學(xué)科內(nèi)的相關(guān)理論、學(xué)科思想方法聯(lián)系起來，進而找到解決問題的途徑。思考數(shù)學(xué)問題能力既是提出問題的要素，又體現(xiàn)在是否正確解決問題的過程中，是中小學(xué)數(shù)學(xué)教學(xué)目的與學(xué)生數(shù)學(xué)學(xué)習(xí)活動特點的主要內(nèi)涵，是學(xué)生開展探究性學(xué)習(xí)的要素。這也強調(diào)了理性思維的重要，說明我們小學(xué)數(shù)學(xué)教學(xué)要注重培養(yǎng)學(xué)生的思考能力。

同時，數(shù)學(xué)思考與數(shù)學(xué)思想方法相輔相成。而數(shù)學(xué)基礎(chǔ)知識與數(shù)學(xué)思想方法又是數(shù)學(xué)教學(xué)的兩條主線。在數(shù)學(xué)知識的發(fā)生、發(fā)展與應(yīng)用過程中都以數(shù)學(xué)思想方法的形成作為數(shù)學(xué)教學(xué)高層次的追求，數(shù)學(xué)思想方法是數(shù)學(xué)知識的骨架與肌肉，是數(shù)學(xué)知識結(jié)構(gòu)的活力與靈魂。數(shù)學(xué)教材的每一章節(jié)乃至每一道題，都體現(xiàn)著數(shù)學(xué)基礎(chǔ)知識與數(shù)學(xué)思想方法的有機結(jié)合。早在1989年NCTM（全美數(shù)學(xué)教師協(xié)會）發(fā)表《中小學(xué)數(shù)學(xué)課程與評估標準》就提出“學(xué)會數(shù)學(xué)思想方法”是“有數(shù)學(xué)素養(yǎng)”標志的五項條件之一。因此，在教學(xué)中教師要認真研讀教材，結(jié)合教學(xué)內(nèi)容引導(dǎo)學(xué)生在探究學(xué)習(xí)中，學(xué)會數(shù)學(xué)思考并滲透相關(guān)的數(shù)學(xué)思想。

數(shù)學(xué)教學(xué)重在發(fā)展學(xué)生的數(shù)學(xué)素養(yǎng)，這就得十分關(guān)注數(shù)學(xué)思考與數(shù)學(xué)思想方法的滲透。而數(shù)學(xué)思考與數(shù)學(xué)思想應(yīng)該在學(xué)生探究知識的過程中落實。

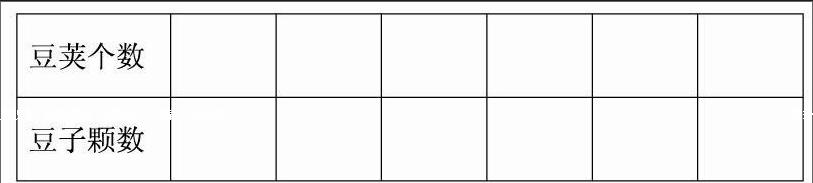
如人教版二年級上冊《表內(nèi)乘法》教學(xué)內(nèi)容中，《6的乘法口訣》教學(xué)情境是出現(xiàn)6個豆莢，隱藏的條件是每個豆莢都有6顆豆子這個相同加數(shù)。首先，比起1-5的乘法口訣認識中，實物圖關(guān)于信息的描述提高了一步，有意讓孩子學(xué)會找到隱藏的信息；其次，在實物圖下面以列表形式出現(xiàn)1個6、2個6、3個6、4個6、5個6、6個6的連加過程：

意圖在于為孩子自己結(jié)合已有經(jīng)驗自主探究：列出乘法算式并填寫相應(yīng)得數(shù)，并由此歸納6的乘法口訣。同時，借助這種呈現(xiàn)形式滲透了函數(shù)的思想、對應(yīng)的思想。

而本冊教材在后面《8的乘法口訣》認識中，連加過程則是借助數(shù)軸這個直觀模型，以小狗在數(shù)軸上8個、8個地跳躍形式出現(xiàn)，數(shù)形結(jié)合，突出連加結(jié)果。這又是一種數(shù)學(xué)思想方法的滲透。

又如本冊教材《角的認識》中，通過呈現(xiàn)生活中的角，在學(xué)生大量感知的基礎(chǔ)上，借助多媒體演示逐步抽象出“角”，然后提出問題“這些角怎樣搬到我們的本子上呢？”引發(fā)學(xué)生數(shù)學(xué)思考，進而在學(xué)生思考討論交流的基礎(chǔ)上形成共識，再動手畫角，如此達到發(fā)展學(xué)生形象思維與抽象思維。并在角的大小比較的過程中通過多媒體演示把角的兩邊無限延長，這里既讓學(xué)生獲得比較角的大小的方法，又理解了角的大小與邊的長短無關(guān)，既滲透了符號思想，又滲透了極限思想。

從我們的教學(xué)實踐看，掌握數(shù)學(xué)思想方法是學(xué)生數(shù)學(xué)思考能力提高的根本保證，同時學(xué)生具備數(shù)學(xué)思考的能力有利于促進學(xué)生對數(shù)學(xué)思想方法的理解與應(yīng)用，二者存在辯證統(tǒng)一的關(guān)系。

所以教師要認真鉆研教材，精心設(shè)計教學(xué)，使學(xué)生在對同一系列的內(nèi)容探究中，教師既要逐漸放手，讓學(xué)生結(jié)合已有經(jīng)驗進行數(shù)學(xué)思考，開展有效的自主探究，又要在適當(dāng)?shù)狞c撥下初步學(xué)會數(shù)學(xué)思想方法。讓數(shù)學(xué)思考無處不在，讓探究性學(xué)習(xí)更加深入。從而彰顯數(shù)學(xué)的深刻性、嚴密性、邏輯性。

（責(zé)任編輯 李 翔）endprint