積累數學活動經驗，滲透函數思想方法

王林利

前 思

“認識成正比例的量”是蘇教版六年級下冊第八單元的教學內容，這節課是在學生已經具有比和比例的知識、認識了常見數量關系的基礎上編排的，通過對兩個數量保持商一定的變化，理解正比例關系，滲透初步的函數思想。這部分內容比較抽象，學生不易接受。多年來，教師對這個內容的教學研究積淀了大量資源，其中不乏內涵豐富、風格迥異的經典設計和精彩課堂。

但是，在實際教學中常會見到這樣的場景：教師出示例題中的表格，讓學生觀察表格回答以下三個問題：表中有哪兩個相關聯的量？什么量變化，什么量也隨著變化？它們相對應的數的比值是怎樣的？教師通常認為只要讓學生計算兩個量相對應的數的比值后發現比值不變，就能讓學生體會正比例關系的含義，函數思想就能得到有效滲透。其實，這樣僅僅通過計算得出比值不變的結論，進而歸納出正比例關系的含義，是不能激發學生的內在思維的！學生對找到的規律似懂非懂，知其然而不知其所以然。在這樣的情況下，如果教學設計不能作相應的考慮和調整，那么學生的思維就很容易受到束縛，就難以有效激發學生對數學規律的深入探究和對數學本質的思考。到底如何教學才能真正實現學生思維的轉變，更好地滲透函數思想呢？

立足于上述認識，我對本課的教學目標定位如下：

1.結合具體情境認識成正比例的量的特點，理解正比例的意義，學會根據正比例的意義判斷兩種相關聯的量是不是成正比例。

2.經歷操作、探究、猜想等學習活動，初步體會數量之間相依互變的關系，感受有效表示數量關系及其變化規律的不同數學模型，進一步培養觀察能力和發現規律的能力，滲透初步的函數思想。

實 踐

一、導入新課

1.談話

師：同學們，我們的家鄉常熟是著名的江南水鄉，眾多自然景點春夏秋冬各有特色，喜歡到常熟來旅游的游客也越來越多，誰能來向大家簡單介紹一下我們常熟四季的天氣情況？

學生介紹。

師：對，常熟一年四季分明，1、2月份較寒冷，7、8月份比較炎熱，氣溫隨著月份的變化而變化。

揭示：像這樣，一個量的變化，另一種量也隨著變化的兩個量，我們稱為兩個相關聯的量。（板書：兩個相關聯的量）

2.練習

課件出示：它們是相關聯的量嗎？

（1）王老師的體重和身高；（2）正方形的邊長和面積；（3）圓的直徑和周長。

指名口答。

3.舉例

在數學中，你還知道哪些相關聯的量？（學生交流）

二、新知學習

1.在情境中找特征

師：下面我們進一步來研究相關聯的兩個量，研究汽車行駛的路程和時間這兩個量怎樣在變化，有什么關系。

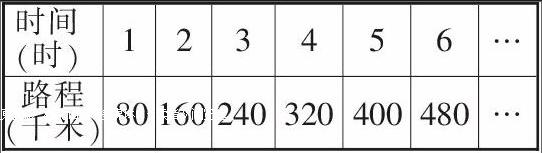
媒體出示：一輛汽車1小時行駛80千米，2小時行多少千米？3小時、4小時、5小時……各行多少千米？

生：80千米、160千米、240千米、320千米、400千米……

根據學生回答，逐步形成下表：

師：觀察上表，想一想：汽車行駛的路程與時間之間有怎樣的關系？把你的發現和同桌交流一下。

生1：時間和路程是兩個相關聯的量，汽車行駛1小時，路程是80千米；行駛2小時，路程為160千米；行駛3小時，路程為240千米……

生2：時間擴大了，路程也隨著擴大，路程隨著時間的變化而變化。

師：現在我們從后往前看，時間由6小時變為5小時、4小時、3小時……路程又是如何變化的？

生：路程由480千米變為400千米、320千米、240千米……

2.用數據分析關系

師：從上面的數據變化情況，你發現了什么樣的規律？同桌進行討論。

生：時間從小到大，路程也隨著從小到大變化；時間從大到小，路程也隨著從大到小變化。

師：這是為什么呢？它們擴大縮小的變化規律是什么？

學生獨立思考。

生：因為速度一樣。

師：是不是這樣？這個速度是誰與誰的比？

生：這個速度是路程和時間的比。

師：這個80實際是什么？變化了嗎？

生：這個80是汽車的速度，是路程和時間的比值，也是路程和時間的商，速度不變。

師：同學們總結得很好。時間和路程是兩種相關聯的量，路程是隨著時間的變化而變化的：時間擴大，路程也隨著擴大；時間縮小，路程也隨著縮小。

3.在想象中形成表象

師：請同學們閉上眼睛想象一下：如果汽車繼續向前行駛，7小時，8小時……想象一下路程在怎樣變化，請用手勢表示出來。

學生的手勢如下：

師：請你把汽車行駛的時間想象得再細一些，0.5小時、0.6小時、1.2小時、1.3小時……路程是怎樣變化的？

學生的手勢都變成了第一種。

師：請你根據自己的想象，再來說一說路程和時間在怎樣變化？

揭示：當路程和時間的比值總是一定（也就是速度一定）時，我們就說行駛的路程和時間成正比例，路程和時間是成正比例的量。今天我們就來研究“成正比例的量”。（板書課題）

4.選情境辨圖像

出示：根據圖像判斷，下面哪一幅圖能表示出汽車勻速行駛過程中行駛的時間和路程？

交流揭示：“汽車勻速行駛”的圖像是一條向上的直線，因為速度不變，所以隨著時間的增加路程也在相應增加。

三、練習鞏固（略）

后 想

反思本課之所以能取得點滴突破，主要就是圍繞學生在認識正比例關系時的認知障礙處，作了有針對性的處理。

一、活用素材，積累數學活動經驗

在我們的現實世界中，到處都存在數學現象。在本節課的課堂導入部分，從認識生活中變化的量開始，讓學生觀察常熟地區氣溫和月份之間的變化情況，感受變化的量在生活中無處不在，讓學生體驗關聯，再順水推舟地把這種生活中的關聯遷移到數學上。學生認識到本節課的研究對象是一組變化的量，研究目標是變化的量之間存在的關系。這樣，研究對象和研究目標明確，有利于學生思維方式的初步轉變。

二、數形結合，滲透函數思想方法

數學是研究數量關系和空間形式的科學。在教學素材的選擇上，注意表格、圖像和函數表達式結合使用，實現數與形的有機結合，培養學生在符號語言與圖表語言之間進行轉換的能力，有利于滲透函數思想方法。

1.著力于數據的動態形成過程

“數學基本活動經驗”作為教育目標提出，是基于動態的數學觀，把數學看成是人類的一種活動，是一種充滿情感、富于思考的體驗和探索活動。在例題中，以動態呈現的方式，在對話與思考中逐步得到數據。在此過程中，學生能感受到數量的變化和發展，感悟數量變化的規律，體會“汽車行駛的時間在變化，路程也隨著變化”。同時，通過追問，讓學生在思維沖突中思考制約這兩個量變化的重要因素——速度，并通過深入對話，讓學生深刻理解當速度不變時，汽車行駛的時間確定，行駛的路程也隨之確定。由此體會數量之間相互聯系、相互制約的關系，感悟一個量的確定能帶來另一個量的確定。

2.著力于圖像的想象和分析過程

函數思想方法是小學數學教學中首推的重要思想方法。在新知學習部分，分別安排了在情境中找特征—用數據析關系—在想象中形成表象—選情境辨圖像等數學探究活動，引發學生的數學思考，激發學生的認知沖突，促進學生深刻思考：“怎樣能證明你的猜測是正確的？”這個問題意在引導學生將自己的思維過程以外顯的方式表達出來。學生通過討論、辨析，將形象思維、抽象思維活動相結合，這樣的數學活動，發展了學生的數學思維和空間觀念。

在學生認識了成正比例的量的特點之后，通過呈現具有較強現實性的問題情境，讓學生感受圖像變換與數量變換之間的關聯。由于數形結合，使得變量之間的抽象關系顯得更加形象，更加直觀，深化了學生對正比例關系的理解，促進了學生對函數思想方法的領悟。