借助幾何直觀教學 積累數學活動經驗

王衛東　潘淑芬

數學活動經驗是《數學課程標準》（2011年版）提出的核心概念之一。重慶師范大學仲秀英教授認為：“數學活動經驗可以理解為學生從經歷的數學活動過程中對活動的感受、體驗、感悟，以及由此獲得的數學知識、技能、情感與觀念等組成的有機組合性經驗。”其實，就經驗本身而言，就是一種感受、體驗、感悟，具有較強的內隱性，所以在教學過程中，教者有時難以把握、調控與評價。為此，我們有必要借助幾何直觀進行教學，使內隱的數學活動經驗得以外顯，進而再根據這些外顯的“證據”，對數學活動經驗進行具化、調控與提升，從而實現數學活動經驗的有效積累。

一、借助幾何直觀具化數學活動經驗

數學學習離不開直觀形象的思維，積累數學活動經驗的過程更是如此。借助幾何直觀教學，我們可以把復雜的問題變得簡明、形象，與此同時，也可以將學生在學習過程中的感受、體驗與感悟變得具體、直觀。從而在數與形、圖與形的溝通與聯系中，讓那些看似虛無飄渺的數學活動經驗變得看得見、摸得著了。

片段一：在教學《倍數和因數》時，教者開展了這樣的教學活動。

師：你能找出12的因數嗎？請在數軸上表示出來。

師生交流，在數軸上標出12的因數。

師：同學們，仔細觀察數軸。看到這些因數，你想到了什么？

生1：我發現12最小的因數是1，最大的因數是12，也就是它本身。

生2：我認為12的因數可以成雙成對地找出來，如1、12，2、6，3、4。

生3：對，而且每組的兩個因數還越來越接近。

……

生：老師，我有一個疑問：是不是所有的數，因數的個數都是偶數個呢？

師：你的想法很有價值，那到底對不對呢？我們不妨舉些例子來試一試。

思考：很難想象，一個數的因數能與幾何直觀圖產生什么樣的“化學反應”，然而，在上述教學環節中，教者卻巧妙地借助數軸這個形象直觀的載體，將學生的數學活動經驗進行了定格與凝結。通過數軸上點與點之間的關系描述，教者簡單有效地捕獲到了學生思維發展的軌跡：最大因數與最小因數的特點、因數的分布特征、尋找因數的方法、因數個數的規律探究……更為重要的是，借助幾何直觀的“具化”作用，學生在思維的激烈碰撞過程中，從模糊到明晰、從簡單到復雜、從模仿到內化，他們慢慢地積累了發現問題的經驗、思考問題的經驗以及解決問題的經驗。

二、借助幾何直觀調控數學活動經驗

積累基本數學活動經驗的過程也是數學活動經驗的內涵之一。一般來說，積累基本數學活動經驗的過程大致需要經過經歷、內化、概括、遷移的過程。在這樣的過程中，我們需要借助幾何直觀來發揮教師的主導作用，適時對積累數學活動經驗的過程加以調控。

片段二：在教學《解決問題的策略——轉化》時，教者開展了這樣的教學活動。

師：剛才大家用通分的方法計算出了+++的結果，這里的通分，其實就是一種轉化的策略。除了通分以外，你還有其他方法嗎？（學生思考）

師：觀察這幅圖（圖1），想一想，它與算式之間有什么樣的聯系？（學生討論）

師：現在你有什么新想法？

生：我想這樣計算：1-=，因為陰影面積=總面積-空白面積。

師：你們認為呢？

生：我認為很巧妙！有了這幅圖，可以把加法轉化成減法來計算。

生：是的，用圖形來表示算式，很好理解。

師：既然借助圖形來解決問題這么好，那是不是在任何情況下都能使用它呢？

（學生思考、討論）

生：我認為把算式轉化為圖形也有一定的局限性。大家看，這里陰影部分的面積之間都有著2倍的關系：是的2倍，是的2倍……

師：那是不是說，只要相鄰加數是兩倍的關系，我們就能借助這樣的圖去思考呢？

生1：是的，比如說++++（學生邊說邊畫圖）就可以轉化為1-。

生：我也想了個算式：+++++…+=1-。

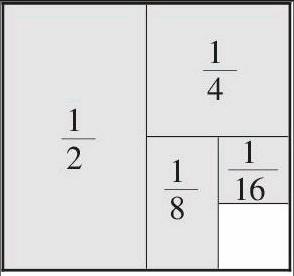
師：有道理。觀察下面的圖（圖2），看看有什么新發現？

生：這里的加法雖然不是從開始加起的，但相鄰加數之間仍然有著兩倍的關系，我認為可以這樣轉化：1--=。

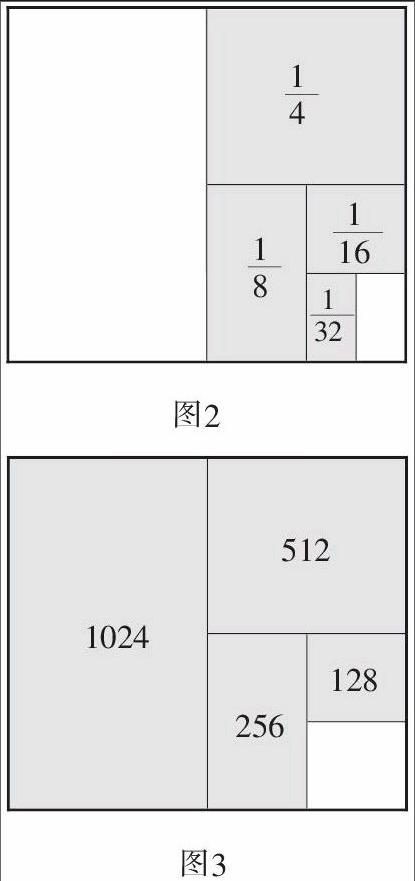
師：聰明！同學們受到他的啟發，現在看到這幅圖（圖3），你又有什么想法呢？

生1：我發現這樣的轉化方法還能用在整數的加法上，只要相鄰加數存在著兩倍的關系。

生：是的，這里的轉化策略不僅適用于整數、分數的計算，小數也可以。

思考：在上面的教學片段中，教者借助幾何直觀開展了三次教學調控。在第一次調控中，教者引導學生將算式+++與圖1相聯系，使他們認識到這類算式中加數的特點，積累了數形結合的思考經驗，感悟了“轉化策略也有局限”的探究經驗。在第二次調控中，教者借助圖2，對+++進行了變式與拓展，幫助學生積累了分析比較、靈活運用的經驗。在第三次調控中，教者再次借助圖3引導學生將數學活動經驗進行了正向遷移，幫助他們積累了猜想驗證、歸納推理的經驗。

從圖1、圖2到圖3，在教師的適時調控之下，學生經歷了不同層次的經驗積累，從知識經驗、技能經驗，再到數學思想方法的經驗，他們在質疑與反思中進行了自我內化與建構。

三、借助幾何直觀提升數學活動經驗

學生需要掌握什么樣的數學活動經驗？是知識的經驗、技能的經驗，還是關于數學思想方法的經驗？毫無疑問，這些數學活動經驗我們都需要，數學教學離不開知識，在知識的學習過程中可以培養學生的能力，感悟數學思想方法。多年以后，知識可能會遺忘，技能可能會生疏，數學思想方法也可能會淡去，既然如此，那什么樣的數學活動經驗才是學生受用一生的經驗呢？

片段三：在教學《乘法分配律》時，教者開展了這樣的教學活動。

1.師：你能用自己的語言來說說什么是乘法分配律嗎？（學生互相交流）

師：大家已經知道了乘法分配律，那你能用更簡單的方法表示出來嗎？

學生嘗試用不同的方法表示：（我+愛）×學=我×學+愛×學；（△+□）×○=△×○+□×○；（a+b）×c=a×c+b×c……

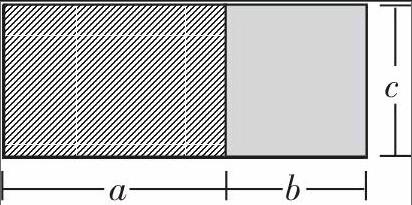
2.出示：

師：你能用兩種不同的方法表示出這個圖形的面積嗎？

生：（a+b）×c或者a×c+b×c。

師：觀察這幅圖和兩個算式，你想到了什么？

生：（a+b）×c=a×c+b×c。

生：哦，這就是乘法分配律！

師：是的，這幅圖就蘊含了乘法分配律，而乘法分配律也可以用這幅圖來表示。大家看，同樣是乘法分配律，從不同的角度來審視，卻有著不一樣的精彩。其實，生活中也是如此，我們要學會從不同的角度來分析問題、解決問題，只有這樣，我們的認識才會更全面，思考才會更有價值。

思考：在上面的教學環節中，為了闡述乘法分配律，教者設計了三個教學階段。先用語言描述規律，然后用漢字、圖形、符號來表示規律，最后用求長方形面積的圖形來表示規律。這其中，教者巧妙地借助幾何直觀將乘法分配律與圖形進行了有機結合，實現了乘法分配律的表達層次由低級到高級，表達形式由單一到多元的經驗積累。與此同時，教者還引導學生從知識的文本中跳出來，引領他們用數學的眼光來觀察世界，認識世界——“我們要學會從不同的角度來分析問題、解決問題，只有這樣，我們的認識才會更全面，思考才會更有價值！

數學是一種智慧，成尚榮教授認為：“數學教育要‘為智慧的生長而教。”因此，數學活動的經驗不能禁錮于知識與技能的經驗，也不能止步于思想與方法的經驗，我們理應幫助學生造就智慧人生的經驗。在上述三個教學片段中，教師引導學生跳出了數學知識的文本經驗，跨過了數學思想方法的經驗，感悟了人生智慧的經驗。從知識走進方法，從思想走近智慧，借助幾何直觀，數學活動經驗的積累由此得到了質的提升與飛躍。