“經驗之塔”與體驗性網絡課程——數學方法論課程的實踐研究

張映姜

（湛江師范學院 數學與計算科學學院，廣東 湛江 524048）

數學思想方法是數學的精髓、靈魂.數學學習不僅僅是知識的學習，更是數學思想、數學方法的學習.思想方法是數學教學的基本原則.湛江師范學院開設了《數學方法論》課程.期待增強高師學生對數學思想方法的理解，增強思想方法對數學教學內容的組織，促進數學解題策略的形成，豐富師范生數學經驗，有效地促進高師學生的教師專業成長.思想方法不同于數學知識，數學思想具有觀念性特點，數學方法具有程序特征，由于受傳統教學媒體的局限，課堂上很難展示經典案例的生動性，較難展現方法的程序性、過程性，學生活動參與性較弱.如今，網絡媒體為《數學方法論》學習提供了較好條件，戴爾的經驗理論為教師選擇合適的媒體資源、采用恰當的課堂學習方式提供了某些參考的理論依據.多年的《數學方法論》教學實踐說明，交互式的動畫、可參與的網絡實驗等是課程《數學方法論》學習的重要資源，經典的案例凝聚了歷史文化，創設了濃郁的數學文化情境，高師學生參與性增強了，學習體驗增加了.這些是傳統教學媒體無可比擬的.

1 戴爾的“經驗之塔”理論

數學思想、方法是主觀對客觀規律的反映，是對客觀世界一般規律的概括和總結，但仍離不開人的主觀經驗.對數學思想方法的認識終究是人的認識，離不開實踐活動.波利亞認為，學生的學習從經驗開始.“大多數最美妙的數學靈感來源于經驗”（馮·諾依曼）.“我們真正的老師是經驗和感覺”（盧梭）.這充分說明經驗在學習中的重要性.許多專家相當重視數學經驗，尤其是數學思想方法方面的創新活動經驗.只有當數學思想和數學知識作為一個環節歸入個人經驗時，才能被理解和掌握.所獲得的數學方法的經驗影響數學知識的組織、策略的運用以及對數學的認識，也將影響高師學生的教師專業成長[1].

“經驗之塔”理論認為，學生的學習經驗可分為做的經驗、觀察的經驗、抽象的經驗.如圖1，學生“做的經驗”處于“塔”的底部，是最直接、最具體的經驗；其次是觀察的經驗，位于“塔”的中部；立于“塔”頂是最抽象的經驗，

即視覺、言語符號的經驗.學習從直接經驗開始，并由具體經驗到抽象經驗.但學習并不總是遵循從直接經驗到間接經驗.戴爾的經驗理論也不能解決技能的訓練問題，智慧技能和動作技能需要親自操作、反復訓練才能形成經驗、熟練掌握；電子的虛擬操作替代不了黑板、白紙上的推演，電腦演示替代不了真實的科學實驗[2].多媒體技術、網絡信息技術在20世紀末才得到廣泛運用，戴爾《視聽教學法》中的“經驗之塔”理論不可能預見動畫圖片、網絡實驗等媒體對學生知識經驗的促進作用.現代媒體畢竟是高師學生獲得知識經驗的重要方式之一.尤其是，當不能獲得思想方法的直接經驗又不能較好地形成思想方法抽象經驗時，可參與交互的網絡實驗、互動的動畫、表現力強的媒體模型等能讓學生獲得具體的、間接的替代經驗.網絡信息資源遠遠不只是提供形成“觀察”經驗的學習媒體，在很大程度上還提供形成“做”的經驗以及“抽象符號”經驗的學習媒體.

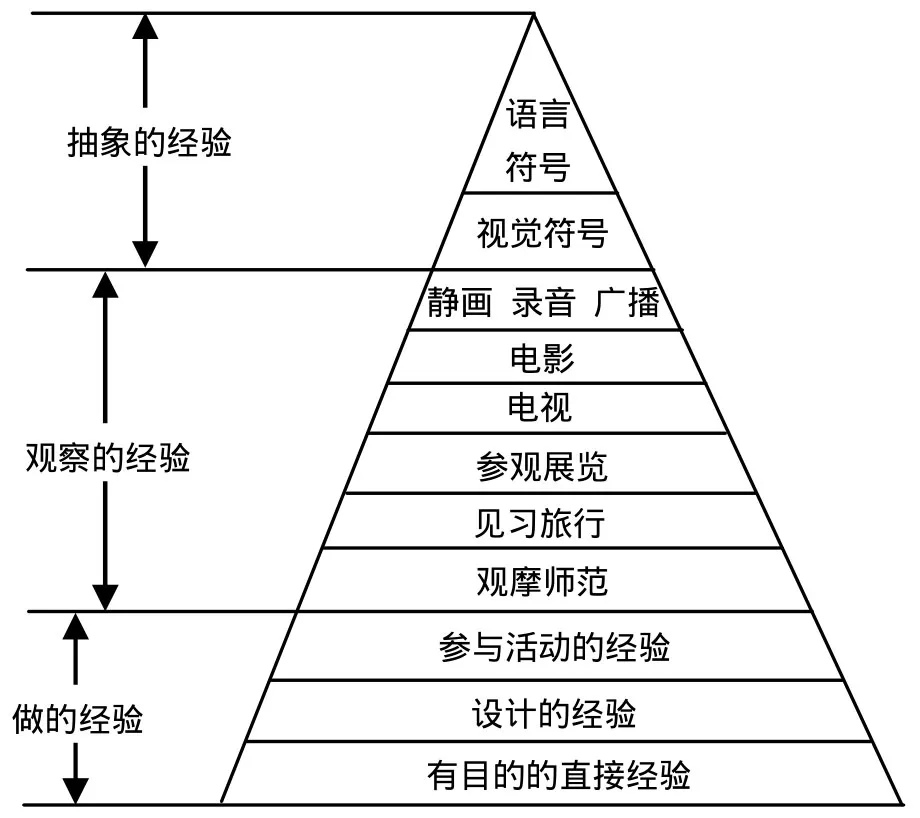
圖1 經驗之塔[3]

2 豐富數學方法經驗的網絡資源

戴爾的經驗理論對于課程《數學方法論》學習資源的選擇具有指導作用.經驗來源于實踐、源于體驗.教育是經驗的改選重組.數學的思想方法以數學經典案例為載體，通過網絡資源進行傳遞.網絡媒體資源實現數學思想、數學方法可視化、操作化，使高師學生有了直觀生動的認知體驗，更深入地理解數學思想方法的涵義，更好地獲得思想方法的經驗，并使經驗具體化.數學變換借助七巧板幾何圖形的變換、函數圖象的變換等進行學習，理解數學變換方法；迭代法的學習借助河內塔實驗、勾股樹等經典案例進行.類比法通過三角形與圓等圖形的類比、棱錐與球等圖形類比進行學習.數學歸納法的理解、掌握需要通過多米諾骨牌的（網絡）視頻，生動再現數學歸納法的初始條件及遞推關系.現代媒體往往能提供數學經典案例，形式多樣的、生動直觀的網絡素材，能供參與的網絡資源，虛擬參與得到“直接經驗”，通過觀察獲得“間接經驗”.具體地，主要有3種網絡學習資源.

2.1 能形成“做的經驗”網絡交互資源

通過網絡系統的虛擬場景增強教學媒體的真實，為高師學生構建可視化的“真實場景”.這種可視化的“真實場景”能讓高師學生獲得與真實生活中相似甚至相同的認知體驗，獲得“做的經驗”.網絡上共享的七巧板的拼圖、拋硬幣的實驗、函數圖象的變換等資源可人機交互，動手操作，參與活動，進行觀摩示范，以及數學設計.通過這些可參與的網絡資源，親手點擊鼠標，親自拼一拼，試一試，體驗思想方法.讓學生擺一擺，拼一拼，探索數學方法的規律.讓學生“做中學”、“玩中學”，改變“聽中學”、“看中學”的學習形式，讓學生獲得“直接經驗”；特別是可交互的網絡資源，給學生提供動手實踐的機會，增加做的環節，容易產生最直接的、難以忘記的學習經驗.交互的學習資源能促進學習過程中高師學生的深度參與.

2.2 能形成“觀察的經驗”的圖形資源

觀察是重要的學習活動.戴爾認為，經驗源于觀察.實踐表明，許多經驗來自于觀察，觀察依賴于情境，即經驗源于情境中的觀察.特瑞赤拉曾證實：83%的信息通過視覺獲得.視覺獲得的經驗信息最多.“一切知識都從感官開始的”（夸美紐斯）.人類獲得更多的是間接經驗.高師學生通過幾種感官交互，獲得思想方法的“觀察經驗”，有了身臨其境的認知體驗.觀察活動有助于對數學思想方法經驗的獲得.網絡能提供許多便于觀察的資源.生動活潑、形象直觀的網絡圖片展示或簡潔明快的網絡視頻，提供學生觀察的機會，獲得觀察的經驗；如圖解、模型、圖表、示意圖，這些視覺符號有助于學生的觀察，利于抽象經驗的進一步形成，圖片、動畫等形象生動具體，便于觀察，豐富學生的觀察經驗.利用圖解、模型、圖表、示意圖等直觀圖形，構建知識學習的直觀情境，把抽象的知識化為具體、形象的、可感知的東西，把學習內容、對象展現在學生面前，讓學生幫助學生理解概念，通過多種外部刺激迅速感知知識，形成形象性知識，使抽象知識具體化、過程化，深奧的知識形象化、趣味化，讓學生通過多種刺激迅速感知知識，把握知識的意義，形成生動的知識，促進學習遷移.

2.3 歷史悠久的經典案例能形成數學方法符號經驗

數學的歷史文化影響學習經驗的獲得.文化是通過教育進行傳承.文化的教育歸根結底是關注人的發展，重視人的因素.社會文化因素影響觀察的視野.愛因斯坦說，“正是理論決定什么是可以觀察的.”歷史的沉淀形成了人類豐富多彩的文化.知識的歷史文化性無疑促進學生觀察、體驗及經驗的獲得.所以，歷史文化體驗是數學思想方法經驗的又一個特色.拋硬幣的實驗、七巧板拼圖等，都是數學上的經典案例，它們浸潤著數學悠久的歷史與純美的文化，成為數學方法論的學習資源，引導學生活動思考，欣賞數學文化，品味悠久歷史，獲得數學經驗，豐富方法內涵.學生通過體驗性學習活動，增強學習體驗，形成并強化數學知識經驗.

3 經驗理論下數學方法的網絡學習方式

網絡信息、多媒體技術為數學思想方法的學習活動給予了充分的支持.經驗理論是數學思想方法網絡學習遵循的主要依據.通過網絡學習資源，讓高師學生既可獲得“觀察的經驗”又可獲得“做的經驗”，并進一步促進“抽象的經驗”的形成，實現了思想方法在“做、觀察、抽象”3種層次經驗的交融，實現高強度的認知刺激和最大限度的體驗，拓展數學創造性思維，達到了更有效的學習效果.利用網絡學習資源，學生直接參與，獲得具體經驗，豐富做的經驗，或通過圖象觀察獲得替代經驗；或通過符號的學習，獲得符號表示的經驗.操作探究、設計學習，學生獲得直接經驗；示范觀摩、案例學習，學生獲得間接經驗.通過體驗性學習活動，進行概括總結獲得數學方法，豐富學生個體知識的內涵，完善知識的涵意，掌握數學方法，實現學習目標.

3.1 探究學習

數學研究、學習需要探究、探索，“在人的心靈深處都有一種根深蒂固的需要.這就是希望自己是一個探索者、發現者、研究者，而在兒童的精神世界中這種需要特別強烈”（蘇霍姆林斯基）.實驗法、歸納法、類比法等數學方法的運用是探究學習的有效方式，是在活動中領悟數學方法.探究學習既可以滿足學生對探究的需要，同時又可以幫助學生對數學方法的運用和理解.網絡上有許多共享的數學實驗是課程《數學方法論》探究學習的經典案例.如圖2，這是拋硬幣實驗.通過拋硬幣的實驗，學生能認識隨機實驗的特點，并能解決日常中難以處理的大樣本隨機實驗研究問題，也有助于學生理解隨機觀念.通過實驗探究，學生能發現隨機現象中固有的數學規律，掌握概率思想.利用網上實驗資源，可以讓學生進行實驗、歸納、類比等活動，學會探究學習，有了探究的經歷，滿足探究的欲望，獲得做的經驗，在活動中進行體驗性學習，掌握了數學方法，有了創造性數學活動的經驗，提高數學能力.

3.2 動手操作

動手操作是形成思想方法間接“做的經驗”的重要方式，這也恰好發揮了增強虛擬情境真實性的網絡優勢.如數學變換方法包括幾何圖形的平移、旋轉、對稱，以及函數圖象對稱、位移、伸縮等變換.利用網絡中共享資源參與交互，動手操作，在進行幾何變換、圖象變換操作中掌握、理解數學方法，獲得“直接”經驗，驗證數學結論，提高學習興趣，強化學習動機.為了理解變換思想，可利用函數圖象的對稱變換進行認識，研究函數y=f(x)與y=?f(x)，y=f(x)與y=f(?x)，y=f(x)與y=?f(?x)圖象變換情況，學生親自參與，人機交互，如圖3.y=f(x)與y=?f(x)，y=f(x)與y=f(?x)圖象分別關于x軸、y軸對稱，y=f(x)與y=?f(?x)圖象關于原點對稱.學生分析思考后，發現，這3種函數圖象的對稱變換對于點的坐標的影響只是橫、縱坐標符號的變化，最終概括為關于軸對稱或點對稱兩類.學生思考函數圖象或幾何圖形變換，就能發現數學變換方法的規律.特別是參與操作、動手交互.聽過的可能會忘記，看過的可能會明白，但動手操作過的肯定不會忘，并能深刻地理解、準確地掌握，獲得生動的經驗.對照幾何圖形變換、函數形式的變化，就能獲得幾何變換的經驗，增強幾何圖形經驗的直觀性、生動性，豐富學生的幾何聯想，體驗數學活動，也獲得數學變換的“替代”經驗.

圖2 拋硬幣試驗

圖3 函數圖像

3.3 觀摩示范

依戴爾的“經驗之塔”理論，示范觀摩是高師學生獲得數學思想方法間接經驗的重要方式.對課程中的尺規作圖、對稱、化歸等方法，觀摩示范也是一個有效的體驗學習方式.利用網絡資源中動畫、圖片、圖表、掛圖、幻燈、錄音、錄像、電影、圖解、模型、示意圖等進行示范，展示操作過程，讓學生進行仔細觀察，反復模仿，使學生掌握方法運用的程序，領會數學方法的規律，獲得操作的替代經驗.觀摩示范，既能使學生獲得豐富的感性經驗，加深對事物的印象，又可以激發學生的學習興趣，發展學生的觀察力，加強技能的掌握、理解，增強記憶效果.

如圖4，網絡資源中的圖案設計（www.diyifanwen.com/kejian/chuzhongyinianjishuxuekejian）.賞心悅目的圖案如何制作？圖案的制作展現了尺規作圖的方法，用形象、直觀的、交互式的動畫方式，用圖案制作示范尺規作圖的程序和方法，展示圖案制作過程，如圖5.通過操作示范，讓學生親眼看一看，親自做一做，觀摩圖案的設計思路，觀察圖形制作方式，發現圖形制作奧秘，掌握幾何尺規作圖的方法，獲得替代經驗.

圖4 圖案設計

圖5 圖案制作過程

3.4 數學設計

數學設計也是高師學生獲得數學思想方法替代經驗的重要方式，能有效地提高創造能力.李約瑟說，七巧板是“東方最古老的消遣品”，“其變化之式多至千余.體物肖形，隨手變幻，蓋游戲之具，足以排悶破寂，故世俗皆喜為之”.拿破侖流放時利用七巧板打發時光.七巧板的拼圖游戲能體現數學的平移、旋轉等變換方法.如通過七巧板的數學設計活動，不僅吸引注意力，激發學習動機，增強參與、創造的意識，而且還在拼圖過程中理解其中所運用的幾何變換方法.利用網絡資源中七巧板設計的平臺，進行七巧板的創作，用七巧板拼成吉祥圖案，慶賀節日，游戲娛樂.變化豐富，巧妙搭配，千姿百態.通過7塊板的平移、旋轉等幾何變換，進行數學設計，拼出袋鼠圖案，如圖6.通過七巧板中5塊三角形、一塊正方形以及一塊平行四邊形的平移、旋轉等幾何變換，進行精巧的數學設計，既能體驗幾何變換的思想，獲得變換方法運用的經驗，也能動手設計，培養創新意識，拼出精美的幾何圖案，感悟數學創新.當然，也體驗七巧板的歷史文化.

圖6 七巧板

3.5 案例學習

案例學習是根據特定的要求，對數學中經典的實例進行研究，達到理解知識、掌握方法、獲得體驗的一種方式.針對數學的無窮小方法、類比方法，通過數學中一些經典案例的研究、學習，展示巧妙的技巧，突出鮮明的主題，欣賞解決策略，體驗創新的經歷，獲得替代經驗，從而理解數學思想的精髓，掌握數學方法.案例越經典越好，經典案例有醍醐灌頂的效果.利用經典的案例把學生的學習注意力集中在有趣的論題上，通過生動事例的再現，突出中心論題，反映現實生活場景.這樣，案例就成為傳遞數學概念、數學原理、數學方法、數學家情感的重要方式.通過網上經典的歷史文化案例，如把圓等分割成全足夠多個小扇形，近似于三角形，再拼成一個近似矩形，如圖7，猜測出圓的面積公式，從而展示人類思考的方向，欣賞、體驗人類高超的智慧.或利用三角形與圓的類比，如數學家開普勒一樣思考，如圖8，把長為2πr的圓周n等分，每份長Δ，周長ΣΔ=2πr，當n取相當大的整數時，得到n個高約等于半徑r的近似于三角形，每個近似的小三角形面積為S=Δr；再對所有近似i小三角形進行面積求和∑S=Δr.i

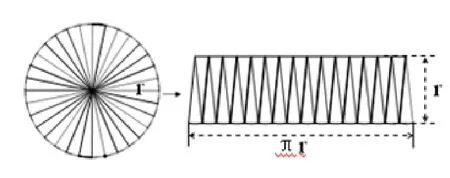
圖7 圓的公面式積推公導式推導

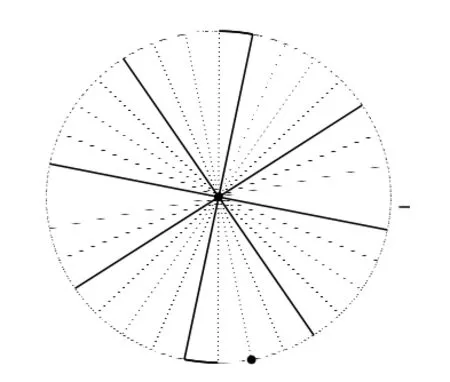
圖8 圖圓與8 三 圓角形類比

于是，得到圓的面積公式

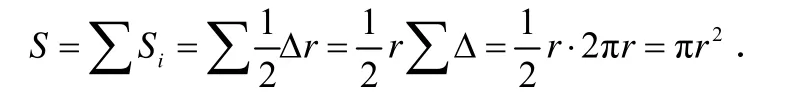
并由此體驗微積分的思想：無限分割—三角形面積—求和—極限[5].類比上述方法，還可類比錐體體積公式，求得球的體積.類比錐體求得球的體積的經典案例學習，能讓人們充分體驗到無窮小方法用于求面積、體積的積分學的思想，展示數學家求旋轉體體積的精巧的思路和方法.通過典型案例進行研究學習，學生在經典案例的文化情景中，掌握思想方法，領悟問題解決的策略，增強想像力，拓寬數學視野，激發或強化學習動機，保持濃厚興趣，形成獨到的見解.

[1]胡典順.數學經驗主義及其對數學教育的啟示，數學教育學報，2012，21（4）：1-4.

[2]王紹銘.經驗之塔前的思考.中國電化教育，2006，（7）：20-21.

[3]耿新鎖.戴爾的“經驗之塔”理論及其現實意義[J].教育史研究，2003，（6）：68-71.

[4]顧越嶺.關于構建數學方法論理論體系的探討[J].數學教育學報，1998，7（1）：53-57.

[5]羅志華.重溫圓的名題，體驗數學文化[J].數學教學研究，2010，（8）：15-18.

[6]曹才翰，蔡金法.數學教育學概論[M].南京：江蘇教育出版社，1989.

[7]鐘啟泉，汪霞，王文靜.課程與教學概論[M].上海：華東師范大學出版社，2004.