幾道高考題背后的圓錐曲線性質

●李金興 ●胡名翔

(蕭山中學 浙江蕭山 311201) (復旦大學 上海 200433)

幾道高考題背后的圓錐曲線性質

●李金興 ●胡名翔

(蕭山中學 浙江蕭山 311201) (復旦大學 上海 200433)

1 從2000年的一道春季高考題說起

2000年普通高校春季招生考試(北京、安徽卷)第22題如下：

如圖1，設點A，B為拋物線y2=4px(p>0)上原點以外的2個動點，已知OA⊥OB,OM⊥AB，求點M的軌跡方程，并說明它表示什么曲線.

因為當OA⊥OB時，直線AB過定點R(4p,0)，所以點M在以線段OR為直徑的圓上，即點M的軌跡方程為x2+y2-4px=0(x≠0)，它表示的曲線是圓(去掉原點).點M是定點O在Rt△AOB斜邊AB上的射影，不妨把點M的軌跡所在的圓x2+y2-4px=0稱為“點O相對于拋物線y2=4px的射影圓”.

本文中，我們作如下定義：以定點P為直角頂點任作一個直角三角形，使斜邊的2個端點A,B都在某一圓錐曲線C上，那么定點P在直線AB上的射影M總在一個定圓C′上，稱定圓C′為定點P相對于曲線C的射影圓.

2 一類顯而易見的推廣

因為過圓錐曲線上一定點作2條互相垂直的弦，聯結另2個端點的直線過定點，所以圓錐曲線上的任意一點都有相對于該圓錐曲線的射影圓.

例如，過拋物線y2=2px上一定點P(x0,y0)作2條互相垂直的弦PA,PB，則直線AB過定點R(x0+2p,-y0)(證明略).此時，點P在Rt△APB斜邊AB上的射影M的軌跡在以線段PR為直徑的圓上，該圓恰是“點P相對于拋物線y2=2px的射影圓”(如圖2).類似地，在橢圓與雙曲線中也有這樣的結論(如圖3和圖4).

圖3 圖4

3 淺嘗輒止的2009年高考題

2009年山東省數學高考理科第22題如下：

(1)求橢圓E的方程.

換個角度看(如圖5)：以橢圓中心O為直角頂點作Rt△AOB，使得點A,B在橢圓上，則點O在斜邊AB上的射影M的軌跡恰為一個圓(即點O相對于橢圓E的射影圓).

圖5 圖6

無獨有偶，2009年北京市數學高考理科第19題如下:

(1)求雙曲線C的方程；

(2)設直線l是圓O:x2+y2=2上動點P(x0,y0)(x0y0≠0)處的切線，l與雙曲線C交于不同的2個點A,B，證明:∠AOB的大小為定值.

換個角度看(如圖6)：以雙曲線中心O為直角頂點作Rt△AOB，使得點A,B在雙曲線上，則點O在斜邊AB上的射影M的軌跡恰為一個圓(即點O關于雙曲線C的射影圓).

4 定點相對于圓錐曲線的射影圓結論的進一步推廣

綜上可知，當定點在某圓錐曲線上或有心圓錐曲線的中心位置時，定點相對于該圓錐曲線的射影圓存在.那么，對于某圓錐曲線所在平面內的任意一定點，只要經過該點能作2條互相垂直的直線都與圓錐曲線相交，是否都有該定點相對于此圓錐曲線的射影圓存在呢？通過幾何畫板作圖觀察發現，結論是肯定的.

如圖7，當點P不在拋物線上時，點P相對于拋物線的射影圓存在(圖中虛線所示).

圖7

如圖8、圖9、圖10所示：對于圓、橢圓、雙曲線，結論也成立.

圖8

圖9

圖10

5 定點相對于圓錐曲線的射影圓存在性的證明

可將推廣后的結論歸納為如下問題：已知平面內圓錐曲線C和定點P，動點A,B在曲線C上且∠APB=90°，求證：點P在直線AB上的射影M總在一個定圓上.

證明分“點P不在曲線C上”和“點P在曲線C上”這2種情況討論.

情況1當點P不在曲線C上時，以點P為原點適當建立坐標系，因為曲線C不過原點，所以圓錐曲線C的方程可化為

同理，因為直線AB不過原點，所以直線AB的方程可設為

此時，直線PM方程為

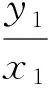
聯立式(1)，式(2)并化為齊次式得

ax2+by2+(cx+dy)(mx+ny)=(mx+ny)2,

即 (b+dn-n2)y2+ (cn+dm-2mn)xy+

(a+cm-m2)x2=0.

(4)

(b+dn-n2)k2+ (cn+dm-2mn)k+

(a+cm-m2)=0,

而k1,k2恰為上式方程的2個根,因此

b+dn-n2≠0且Δ>0.

由韋達定理知

即

a+b+cm+dn=m2+n2,

于是

即

需要補充的是:若a+b=0,此時二次曲線為等軸雙曲線,射影圓褪化成直線cx+dy=1.

(2)若x=0,則點A,B必在坐標軸上，得

可以驗證此時點M也在上述圓(a+b)x2+(a+b)y2+cx+dy=1上.

需要補充的是：如果圓錐曲線與x軸或y軸無公共點，則點A或點B不存在，點M也不存在.

情況2當點P在曲線C上時，同樣以點P為原點建立適當的坐標系，則圓錐曲線C過原點，方程可化為ax2+by2+cx+dy=0.直線AB的方程仍可設為mx+ny=1,則

ax2+by2+(cx+dy)·(mx+ny)=(mx+ny)2.

仿情況1可求得點M的坐標,使得

需要補充的是:若a+b=0,此時二次曲線為等軸雙曲線,射影圓褪化成直線cx+dy=0.

6 對結論的反思反思1

在某些情況下，繞定點P旋轉的2條互相垂直的直線只在一定區域內轉動才能都與圓錐曲線相交，對應的射影M的軌跡只是射影圓的部分弧段(如圖8和圖9中的左圖).

反思2當a+b≠0，c,d不都為0時，方程

(a+b)x2+(a+b)y2+cx+dy=0

表示圓，而當a+b≠0，c=d=0時，方程

(a+b)x2+(a+b)y2+cx+dy=0

僅表示坐標原點(無射影圓).事實上,當c=d=0時，圓錐曲線C的方程可化為ax2+by2=1，點P只能是有心圓錐曲線的中心,即原點.

反思3通常情況下，圓錐曲線的方程以“標準方程”的形式給出，而點P不在原點，此時，射影圓的方程可以利用坐標變換來解決.

例如，求拋物線C:y2=2px上點P(x0,y0)相對于拋物線C的射影圓.

由直線AB過定點R(x0+2p,-y0)的結論知，射影圓圓心為(x0+p,0).而以P(x0,y0)為原點建立新坐標系x′Oy′，則在新坐標系下，拋物線方程為

(y′+y0)2=2p(x′+x0)，

與方程ax2+by2+cx+dy=0相比，得

a=0,b=1，c=-2p，d=2y0,

[1] 胡典順，徐漢文.一種新思路探求一類定點問題[J].中學教研(數學)，2007(10)：28-29.

文獻[1]中“化齊次”的思想方法，該問題可得以巧妙地證明.