探究一道波羅的海數學奧林匹克競賽試題

●

(海南中學 海南海口 571158)

探究一道波羅的海數學奧林匹克競賽試題

●李寧

(海南中學 海南海口 571158)

2011年波羅的海數學奧林匹克競賽中有如下一道不等式試題：

題目設a,b,c,d是滿足a+b+c+d=4的非負實數，證明不等式：

1 證法探究

這是一道常見類型的對稱不等式題.由于已知條件是一次的，可以考慮“化曲為直”，用切線法證明.

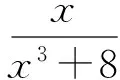
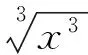
從而

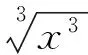
下面只需證明

即

而由均值不等式

得

同理可得

以上4個式子相加，得

從而不等式得證.

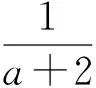
證法4當x≥0時，由九元均值不等式，得

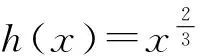
于是

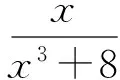
2 題目探究

上面探究了該試題的4種證明方法，同時對其題目本身也可作一番探究.

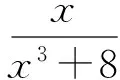
探究該試題的反向，得

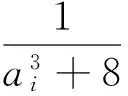
當ai中有一個為n其余全為0時,等號成立.

稍微改變該試題的條件，可得如下變式：

問題3設a,b,c,d是滿足a2+b2+c2+d2=4的非負實數，則

證明當x≥0時,

有興趣的讀者可以探究問題3的另證及推廣.