數學思維的5個品質
——以2013年中考典題的破解為例

●

(晉州市實驗中學 河北晉州 052260)

數學思維的5個品質
——以2013年中考典題的破解為例

●苑建廣

(晉州市實驗中學 河北晉州 052260)

數學與思維猶如一對夫妻，共同演繹著千古不朽的神話.“數學是思維的體操”，數學活動的核心是思維活動，數學的存在和發展離不開思維，都要通過思維來表現.反過來，數學又是思維的工具.在探索、研究和應用數學的過程中，思維品質也在發生著量和質的變化，并因此標志了數學修養之深淺.本文對數學思維品質的5個方面進行剖析，并附例以2013年中考典題.望各位同仁窺斑見豹，體味數學思維的無窮魅力.

1 思維的深刻性

思維的深刻性是指在分析和解決問題的過程中，能夠透過表面現象認識和把握問題的實質及其相互關系，揭示規律，追根溯源，或將已有方法和結論拓展、變換、推廣，得到更深刻的結果，謂之“思維的洞察力和穿透力”.思維的深刻性是一切思維品質的基礎，主要表現為以下幾個方面：

(1)對數學概念理解透徹，形成科學合理的概念域和概念系；對數學事實掌握清楚，形成科學合理的命題域和命題系.頭腦中內化的數學知識是系統化和網絡化的，猶如一棵倒掛的樹：各知識點在這個網絡中處于一定位置，知識點之間呈現出可推理的結構關系，并因此蘊含了思維方法和策略.

(2)具備良好的數學交流能力和符號意識，可以自如地將其他語言等價翻譯為數學語言，發現或抽象出數學模型，實現橫向或縱向數學化.

(3)能自覺運用分析、比較、抽象、概括等思維操作，發現形異質同的數學對象之間的內在聯系.

(4)即使解決問題的條件不是明確給定的，也能不受表面現象的困擾，從表象中挖掘隱含條件，為解決問題作出適當的鋪墊.

(5)在解決具體的問題后，能主動自覺地去尋找具有普遍意義的方法、模式，將思想、方法、結論等概括、遷移、推廣到一般情境中去.

(2013年山東省煙臺市數學中考試題)

圖1

分析通常采用割補法，化非標準圖形為標準圖形，按“S陰=S扇形BAC+S正方形EFGB+S△CEF-S△AGF”求解.設正方形EFGB的邊長為a，則

CE=4-a，AG=4+a，

于是

這個結果正好是扇形BAC的面積！那么，圖中陰影面積是否能轉化成扇形BAC的面積呢？容易想到聯結BF,AC，易證BF∥AC，可見△ACB與△ACF是“同底等高”的，面積也相等，于是S陰=S扇形BAC，思路被大大優化.從中可知，陰影部分的面積與點E在線段BC上的位置(即正方形EFGB的大小)無關，是定值4π.繼續思考，還可發現：

變式1如圖2，把“點E在BC上”變為“點E在BC的延長線上”時，亦可得陰影部分的面積為4π.

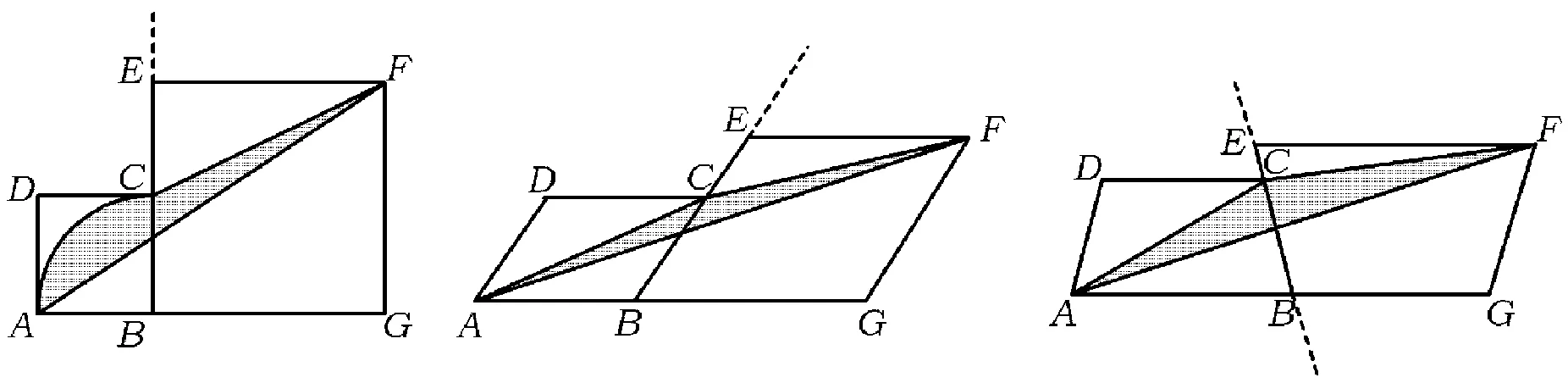
圖2 圖3 圖4

變式2如圖3，當四邊形ABCD和四邊形EFGB均為平行四邊形，且2個平行四邊形相似，點E在射線BC上運動時，陰影部分的面積為平行四邊形ABCD面積的一半.

變式3如圖4，當四邊形ABCD和四邊形EFGB均為等腰梯形，且2個等腰梯形相似，點E在射線BC上運動時，陰影部分的面積等于△ABC的面積.

變式4如圖5，當△ABC∽△EDB,點E在射線BC上運動時，陰影部分的面積等于△ABC的面積.

這也是此類圖形的本質所在.

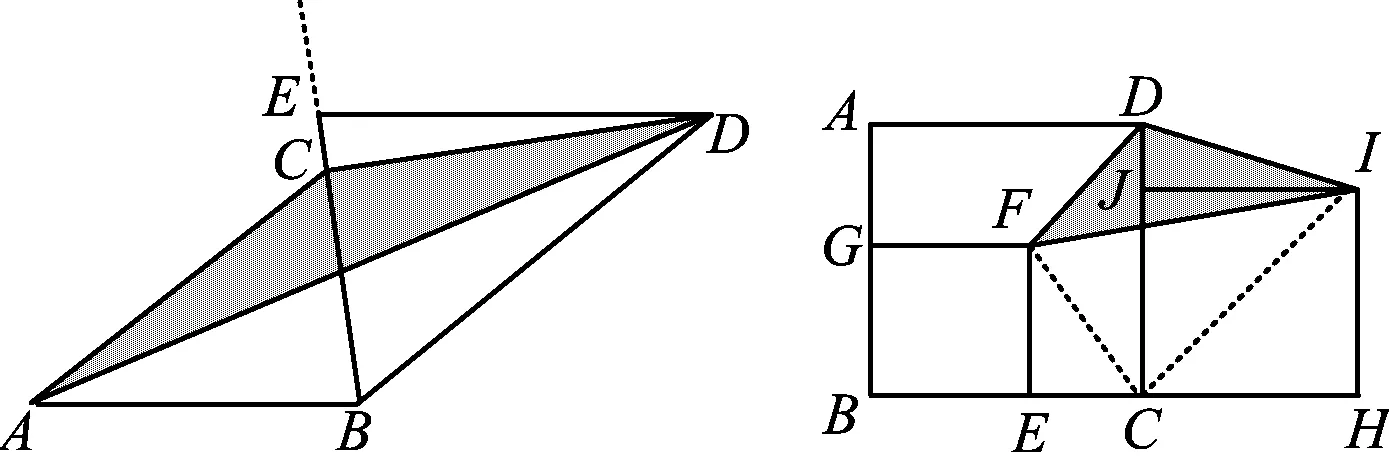
圖5 圖6

變式5如圖6，有3個正方形ABCD，BEFG和CHIJ，其中正方形ABCD的邊長是a，正方形BEFG的邊長是b，當點J在射線CD上運動時，陰影部分的面積等于△CDF的面積,值為a2-ab.

繼續梳理上述問題的辯證關系，按照“從特例到一般”的順序，層層設問，不斷觸及問題的本質，就能設計出一系列非常優秀的探究性問題.

溯本窮源悟真知.在數學學習中，善于透過現象看本質，有利于實現對數學概念和命題的深刻理解.

2 思維的靈活性

思維的靈活性是指因題制宜，活用有關知識多角度尋求問題解決途徑的能力，謂之“思維的發散力和變通力”.主要表現為以下幾個方面：

(1)思維起點靈活.善于全面地看問題，能從與題目相關的各種角度和方向去考慮問題.

(2)心理轉向容易.從正向思維轉為反向思維，特別是對概念正反關系的認識、公式的正反運用、定理與逆定理的靈活使用、解題中分析法與綜合法交替使用時表現自如.

(3)思維轉換迅速.可以不受先前解題方法的影響，克服思維定勢的消極作用及自我心理限制，遇機而變，及時調整思路、方法、技巧，不拘一格、有的放矢地解決問題.

(4)思維過程中善于轉化.可以很容易地化生為熟，把幾個部分看成一個整體，或把一個整體分成幾個部分，也就是聚零為整，化整為零.

(5)概括、遷移能力強.運用規律熟練，善于組合分析，思維有彈性、能跳躍，既能注意把握事物的整體，又不忽視重要的細節，能夠從多層面上捕捉有效信息，廣泛地對比、聯想，在研究問題本身的同時，拓展到相關問題.

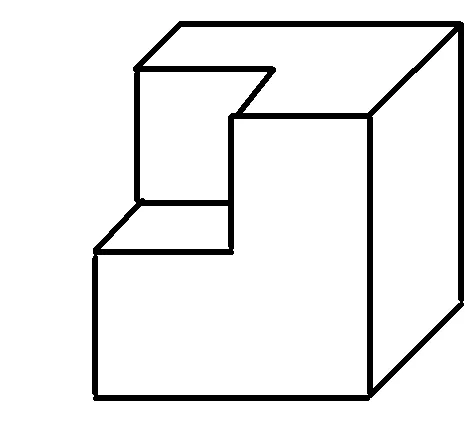
圖7

例2從棱長為2的正方體毛坯的一角，挖去一個棱長為1的小正方體，得到一個如圖7所示的零件，則這個零件的表面積為______．

(2013年山東省棗莊市數學中考試題)

分析整體觀察圖形，利用“平移”實現對問題解決過程的優化，把求“表面積”的問題轉化成求“從上、下、左、右、前、后6個方向看到的視圖面積之和”的問題，極易得到這個零件的表面積為6×(2×2)=24.此時，視圖成為一種解題的工具，只要是從毛坯的一角，挖去一個(任意)長方體，則其表面積均為24，是不變的.解法的趣味性和靈活性都很強.

3 思維的獨創性

思維的獨創性是指思維的結果相對于(自己)已有的認識成果來說，具有獨特性和新穎性，是最難得的思維品質，謂之“思維的發現力和創造力”.主要表現為以下幾個方面：

(1)從事數學活動時，能對數學對象進行獨立的思考，善于發現、提出、分析、解決問題，勇于創新，敢于突破常規的思考方法和解題模式，大膽提出新見解和采用新方法

(2)能從與眾不同的全新角度觀察問題，能在貌似平常的信息中發現不尋常之所在，從而發現隱含的特殊聯系，產生與他人不同的思路和結論.

(3)富于聯想.在解題時主動聯系數學的不同分支、其他學科以及生活實際，以至思維跳躍，經常產生有別于常規的、正統的、創造性的想法.

例3某數學活動小組在作三角形拓展圖形，研究其性質時，經歷了如下過程：

(1)操作發現：

在等腰△ABC中，AB=AC，分別以AB和AC為斜邊，向△ABC的外側作等腰直角三角形，如圖8所示，其中DF⊥AB于點F，EG⊥AC于點G，M是BC的中點，聯結MD和ME，則下列結論正確的是______.

圖8 圖9

(2)數學思考：

在任意△ABC中，分別以AB和AC為斜邊，向△ABC的外側作等腰直角三角形，如圖9所示，M是BC的中點，聯結MD和ME，則MD和ME具有怎樣的數量關系和位置關系？請給出證明過程.

(3)類比探索：

在任意△ABC中，仍分別以AB和AC為斜邊，向△ABC的內側作等腰直角三角形，如圖10所示，M是BC的中點，聯結MD和ME，試判斷△MED的形狀．

(2013年江西省南昌市數學中考試題)

圖10

分析常規思路自然是按部就班，依次完成題目設問，且通常是分別對MD和ME的數量關系和位置關系予以說明.但是，顯然圖8是圖9的一種特殊情形，而圖9與圖10又屬于并列情形，題目本身呈現出“從特例推向一般”、“從一種情形(圖9中向△ABC的外側作等腰直角三角形)向另一種情形(圖10中向△ABC的內側作等腰直角三角形)拓展”的命題模式.參透了這一點，便能作如下處理：

欲證“△DME是等腰直角三角形”，若能證出“∠MDE=∠MED=45°”，則問題得以突破.

如圖9，取AB,AC的中點F,G，聯結DF,FM,EG,GM,DE. 易知∠FDA=∠GEA=45°，于是轉為證

∠ADE=∠FDM，∠AED=∠GEM.

設AB=2a,AC=2b，易得

于是

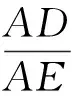
又易證 ∠DAE= 270°-∠BAC=

(180°-∠BAC)+90°=

∠AFM+∠AFD=∠DFM,

于是

△DAE∽△DFM,

故

∠ADE=∠FDM，

同理可證

∠AED=∠GEM.

到此，思路被打通.將其條件強化，則第(2)小題自然得證.

將之遷移到圖10中，易知∠FDA=∠GEA=45°，于是轉為證

∠ADE=∠FDM，∠AED=∠GEM.

仍設AB=2a,AC=2b，可得

于是

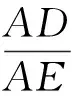
又易證 ∠DAE= (∠DAB+∠EAC)-∠BAC=

90°-∠BAC=90°-∠MFB=

∠DFM，

于是

△DAE∽△DFM，

故

∠ADE=∠FDM，

同理可證

∠AED=∠GEM.

到此，思路再次被打通.

如此處理，顯然超出了命題人所料，是極具創新味道的.正是善于查“平凡中之異象，平靜中之波瀾”，才成就了創新解法.由于特殊情形往往存有無關宏旨的枝節或表面現象，容易掩蓋問題的實質，而一般情形則更能明確地表達問題的本質.因此，有時面對一般化的問題可能更容易求解.就此，希爾伯特有言：“在解決一個數學問題時，如果我們沒有獲得成功，原因常常在于我們沒有認識到更一般的觀點，即眼下要解決的問題不過是一連串有關問題的一個環節.”

4 思維的批判性

思維的批判性是指在思維活動中獨立思考，善于提出疑問，敢于發表不同的看法，嚴格客觀地評價思維的結果和精細地檢查思維過程的品質，謂之“思維的診斷力和甄別力”.主要表現為以下幾個方面：

(1)不會不經思考地附和他人的意見，能堅持自己的合理看法，善于發現問題，明辨是非，不迷信書本和專家，敢于向教師提出質疑;

(2)能夠比較不同對象之間的差異和相似性，辨析容易混淆的概念與形式，對數學對象進行合理分類;

(3)能評估信息資源的可靠性，判斷從一個結論導出另一個結論的充分性，因而發現解題過程或結論中的錯誤;

(4)能在有多種合情思路的情況下，對各種解題思路、方法、策略進行比較，選擇更為合理的方案，從而找出最佳的方法或結論;

(5)在解題時能對全過程進行監控，經常回頭審視自己的解題過程，進行有意識的自我調節，在自我檢查中修正論證的過程和結論．

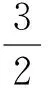
(2013年福建省龍巖市數學中考試題)

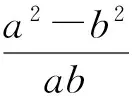
題目難度較大.良好的“數感”固然是重要的，但不斷地對猜想所得進行檢驗和修正，以決定繼續進行下去，還是另覓他徑，更顯重要.思維批判的對象不僅是他人，更是自己.善于自我監控解答過程，“思必有的、有據、有序”，而不是瞎碰亂試，就可在一定程度上避免更多失誤，省時省力.

5 思維的敏捷性

思維的敏捷性是指智力活動的速度，在處理問題和解決問題的過程中，能夠適應迫切的情況來積極地思考，并迅速地作出判斷，謂之“思維的自動化和果斷力”.主要表現為以下幾個方面：

(1)能夠較快且正確地完成對題目信息的理解;

(2)能夠自覺地運用簡便方法，對數字進行快速運算，且“感覺良好”;

(3)能夠迅速地判別出題目的模式，從而縮短解題時間;

(4)能對最近做過的題目有清晰的記憶，迅速反應出解題過程及結果;

(5)能夠迅速判斷，像電腦或機器一樣自動、果斷地執行，在時間緊迫的情況下作出繼續下去或是放棄進行的決策.

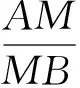
請根據以上結論，解答下列問題：

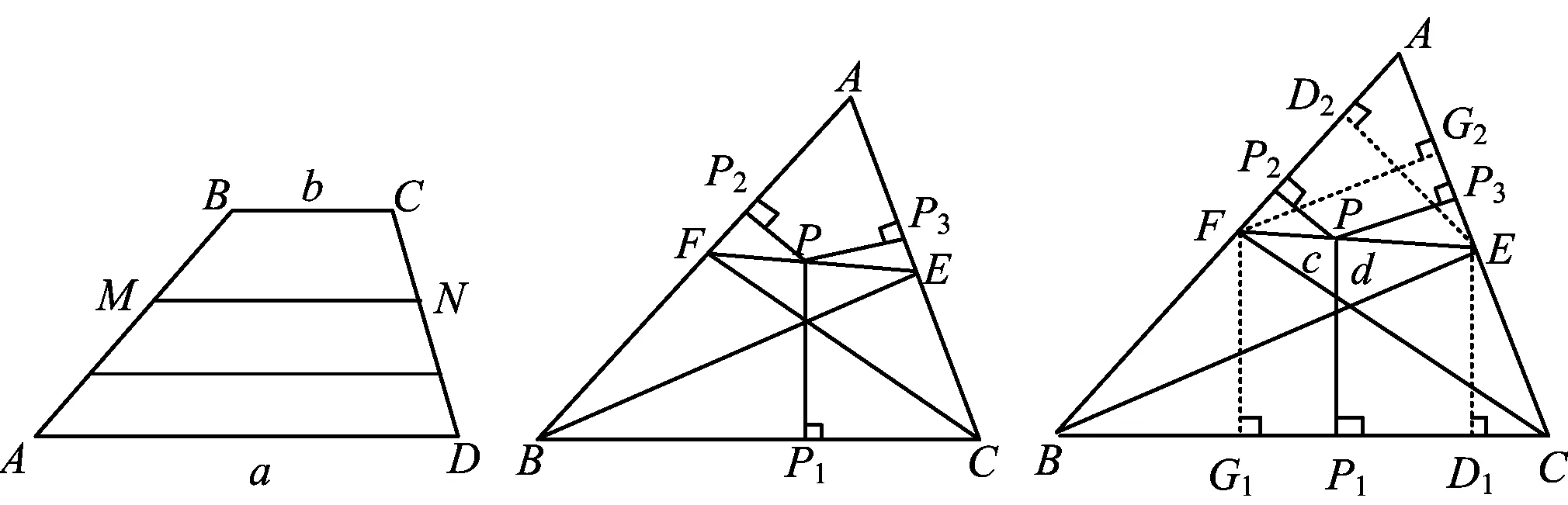
圖11 圖12 圖13

如圖12和圖13，BE,CF是△ABC的2條角平分線，過EF上一點P分別作△ABC三邊的垂線段PP1,PP2,PP3，交BC于點P1，交AB于點P2，交AC于點P3.

(1)若點P為線段EF的中點，如圖12，求證：PP1=PP2+PP3；

(2)若點P在線段EF上任意位置時，如圖13，試探究PP1,PP2,PP3的數量關系，并給出證明.

(2013年四川省樂山市數學中考試題)

分析題目給出了一個新命題(幾何模型)，思維的重點應放在運用新命題解決新問題上.如何“引經據典”，快速完成向模型的化歸，有意識地把新知識、新模型移植轉用到新對象上是解決問題的關鍵.

運用觀察、測量、比較、計算等手段可以“合情”地猜想第(1)小題中之結論可以遷移到第(2)小題中.因此這里我們直接面對第(2)小題，待之證明結束后，將條件強化，則第(1)小題自然得證.結合題設和待證結論，對比圖形構成特點，容易想到如圖13所示的輔助線.設PF=c，PE=d，在梯形EFG1D1中，易得

又三角形可以看作退化的梯形(上底為0)，在△FED2和△EFG2中，易得

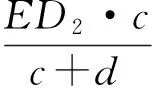
而ED1=ED2,FG1=FG2,故

PP1=PP2+PP3.

實際上，我們雖然分述了數學思維的5個品質，并分別附例詮釋，但是這些品質之間并不是相互分離和隔裂的.恰恰相反，它們是相互滲透、聯系和制約的統一體.深刻性是所有思維品質的基礎，在其支撐下進行發展，避免思維定勢的負面影響，靈活處理，才能產生獨創性見解.加上周密地思慮、批判性地認知和合理地自我監控與調節思維過程，就能形成全面準確的判斷，揭示數學本質和規律.而只有實現了深刻的理解、靈活而富有創造性地思考以及批判性地審問，才能達到心領神會、融會貫通，從而生發出真正的敏捷性，全面提升思維品質，享受數學思維的無限樂趣.

對數學思維的研究永遠是沒有止境的.本文僅僅是在專家理論研究的基礎上補例詮釋，為中學數學教學提供借鑒.不妥之處，誠請不吝賜教.

[1] 中華人民共和國教育部制定.全日制義務教育數學課程標準[M].北京:北京師范大學出版社，2011.

[2] 鮑建生，周超.數學學習的心理基礎與過程[M].上海:上海教育出版社,2009.

[3] 章建躍.數學教育心理學[M].北京:北京師范大學出版社,2006.

[4] 苑建廣.管窺數學思維的若干策略[J].數理化學習:初中版，2012(12):1-9.

[5] 苑建廣.信息轉化——問題解決的核心策略[J].中國數學教育:初中版，2012(3):45-48.

[6] 苑建廣.精心雕琢命題方式切實考查數學能力——2011年中考數學特色題歸類賞析[J].教育實踐與研究:B版，2011(11):7-12.