在問題變式中拓展思維 在合作探究中演繹精彩
——記一堂高三復習公開課的教學設(shè)計與反思

●

(臺州市第一中學 浙江臺州 318000)

在問題變式中拓展思維在合作探究中演繹精彩
——記一堂高三復習公開課的教學設(shè)計與反思

●蔣茵

(臺州市第一中學 浙江臺州 318000)

如何使高三復習課精彩高效?這是每一位數(shù)學教師積極探索的問題,也是新課程改革的目標之一.筆者認為,“問題變式,合作探究”教學模式在高三復習課教學中非常重要.近日,在“臺州市高三數(shù)學復習研討會”上,筆者有幸開設(shè)了一堂主題為“圍繞目標善轉(zhuǎn)化 巧設(shè)點線活運算——基于一類‘直線、拋物線與圓’高考題的探究”的公開課.該課的教學設(shè)計從一個直線與拋物線的基礎(chǔ)問題出發(fā),采用變式教學,層層遞進,演繹為對2011年浙江省高考解析幾何變式題的探究.現(xiàn)將教學設(shè)計及其反思整理如下,以期與同行交流．

1 教學實錄

1.1 問題驅(qū)動,互動探究

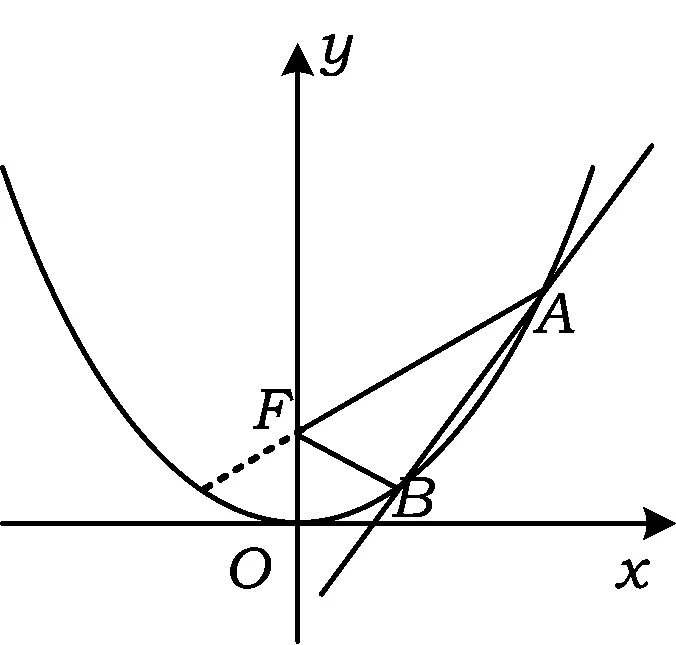
圖1

問題如圖1，已知拋物線C:x2=y,F為拋物線的焦點,A,B是拋物線的2個動點,且A,B在y軸的同側(cè).如果直線FA的斜率與FB的斜率互為相反數(shù),證明:直線AB過定點,并求出這個定點.

設(shè)計意圖引導學生自主讀題,尋找解題目標,在學生求解思路的基礎(chǔ)上完善求解方法,引領(lǐng)學生回顧求解直線與圓錐曲線相交問題時設(shè)直線的2種常用方法,從中領(lǐng)悟函數(shù)和方程思想在求解此類問題中的應用.

(學生思考，展示解法.)

生1：方法1因為k存在,所以設(shè)直線AB:y=kx+b,與x2=y聯(lián)立，消去y得

x2-kx-b=0.

Δ=k2+4b>0,x1+x2=k,x1x2=-b.

下面我不知道該如何求解了?

師：你要證明的結(jié)論(目標)是什么？

生1：要證直線AB:y=kx+b過定點,即找k,b的關(guān)系.

師:這樣的話,能否將條件中kAF=-kBF朝著你的目標去轉(zhuǎn)化呢？

生1：因為x1+x2=k,x1x2=-b,所以找k,b的關(guān)系轉(zhuǎn)化為找x1,x2的關(guān)系,接下來只要將條件中kAF=-kBF向x1,x2去轉(zhuǎn)化即可.

師：請你繼續(xù)給出解答過程.

生1：因為kAF=-kBF,即kAF+kBF=0,所以

即

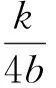
師：很好！這位同學設(shè)的是目標直線,圍繞目標進行合理轉(zhuǎn)化.其他同學還有不同的解法嗎?

由韋達定理,得

y=(xA+xB)x-xAxB,

即

師：很棒!2位同學的解法都很好.方法1從一開始直線的設(shè)法以及中段的解題分析都是從結(jié)論(目標)入手,屬于“分析法”,而方法2恰恰相反,從條件入手,屬于“綜合法”.

1.2 學以致用,變式探究

師：對上述問題的條件能否作些修改,進而得到相應的給論呢？請大家思考.

(學生分組討論,給出下列變式.)

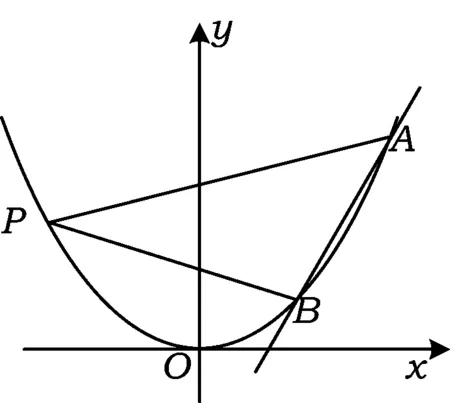
圖2

變式1如圖2，把“F為拋物線的焦點”改為“拋物線上的點P(-1,1)”,試探究:直線AB是否過定點?

生3：用問題中的方法1可得到

化簡得

x1-1+x2-1=0,

即

x1+x2=2,

故k=2.因此直線AB不過定點,但kAB為定值.

生4：用問題中的方法2，設(shè)直線PA:

y-1=k(x+1),

代入y=x2，得

x2-kx-k-1=0.

因為點P在拋物線上,所以xA=k+1,上式中的k用-k替換,從而xB=-k+1.又因為直線AB:

y=(xA+xB)x-xAxB,

所以直線為AB：y=2x+k2-1,即kAB為定值.

生5：不需要聯(lián)立方程,同生4化簡得

即xA=k+1.同理可得xB=-k+1.

師：很好！點的位置變了,但探究的方法沒有改變，而且生3綜合并優(yōu)化了前2位同學的解法.繼續(xù)思考,還能怎么改，能否探究出更一般性的結(jié)論呢？

師:好！我們大家一起來探究.

設(shè)計意圖放手讓學生去改變問題的條件或結(jié)論進行變式探究，鞏固源問題中涉及的數(shù)學方法和探討有沒有更好的解法，從而激發(fā)學生的學習興趣,啟發(fā)學生提出問題,培養(yǎng)學生大膽猜想、小心求證的數(shù)學品質(zhì).

師：太棒了！這組同學運用特殊到一般的思想探究了一般性的結(jié)論.以上我們運用多種方法對一類直線與拋物線的問題進行求解,而在高考題中往往再引入條件(如圓)進行編題.來看這樣一道高考變式題.

變式3如圖3，已知拋物線C:x2=y,圓M:x2+(y-4)2=1,設(shè)點P是拋物線C上一點,過點P作圓M的2條切線l1,l2,交y軸于點A,B,問：是否存在點P,使線段AB被M平分？若存在,求點P的坐標；若不存在,請說明理由.

(2011年浙江省數(shù)學高考文科試題第22題改編)

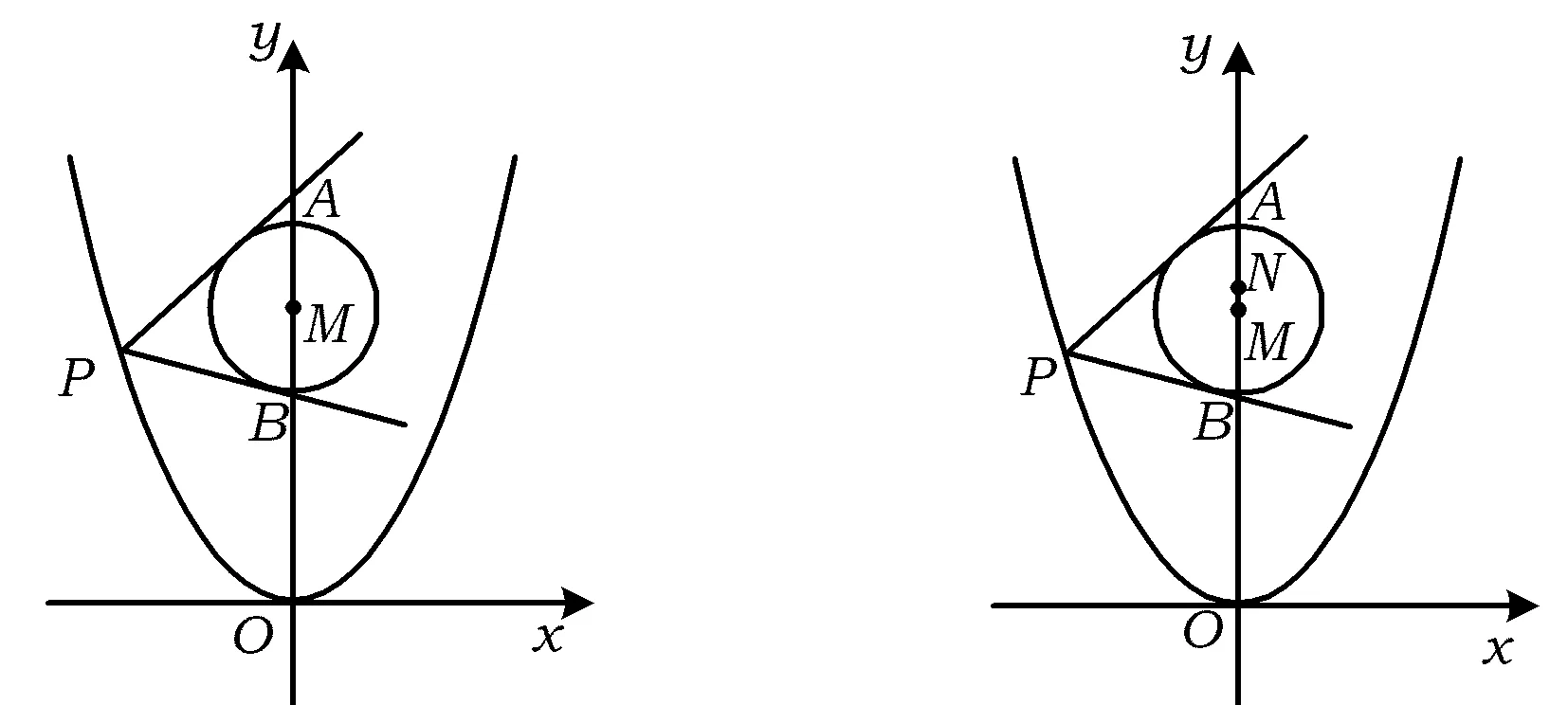
圖3 圖4

生7：根據(jù)圖形的對稱性,若線段AB被M平分,則PM⊥AB，因此點P的坐標為(-2,4).

師：滿足條件的點P只有一個嗎？

生7：還有(2,4).

師：相當精彩！數(shù)形結(jié)合,檢驗了解的個數(shù).

(教師適時利用幾何畫板演示,幫助學生直觀感受點P的位置.)

師:很好!生8的想法不錯,大家想一想,能利用圖形來解決嗎?

生9：由圖4可知點P的縱坐標小于4,而且這樣的點P也有2個.

(教師繼續(xù)利用幾何畫板拖動點P演示.)

師：我們利用圖形猜想了點P的大致位置,能不能利用代數(shù)方法進一步求出點P的具體位置呢？

(學生試解,然后教師選學生“代表”口頭回答,教師板演.)

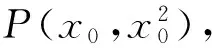
(1)

(2)

按k整理得

設(shè)PA,PB的斜率為k1,k2(k1≠k2),則

不知下面該如何求解了?

師:很好！這位同學把k看作主元整理方程,然后利用韋達定理求解,而且關(guān)注到了運算求解中的整體性.其他同學能否繼續(xù)分析求解?

生11：因為x0與k1,k2找到了關(guān)系,接下去只要找到k1,k2與條件中y1,y2的關(guān)系即可.

令式(1)中的x=0，得

從而

于是

化簡得

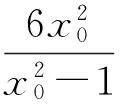
故

即

變式5已知拋物線C:x2=y,圓M:x2+(y-4)2=1,過拋物線C上一點P(t,t2)(-3≤t≤-2)作圓M的2條切線l1,l2,交拋物線于點E,F,求直線EF斜率的最值.

(2011年浙江省數(shù)學高考理科試題第22題改編)

師:請同學們說一說這一變式題怎么解?

生12:“等價轉(zhuǎn)化”目標kEF=xE+xF與t的關(guān)系?xE,xF與kPE,kPF,t的關(guān)系?kPE,kPF與t的關(guān)系(解答過程略).

師：很好！這位同學已經(jīng)學到了如何圍繞解題目標進行合理轉(zhuǎn)化.

設(shè)計意圖進一步強化學生在解題過程中的目標意識、轉(zhuǎn)化能力及函數(shù)方程的思想,突出設(shè)而不求的數(shù)學方法,通過高考變式題為載體內(nèi)化知識,把新學的知識融入到舊的認知體系中去,構(gòu)建新的認知體系.

1.3 探究感受,探究延伸

師:通過這節(jié)課學習,你學到了哪些知識?這堂課體現(xiàn)了哪些數(shù)學思想方法?

生14:我學到了如何巧設(shè)點線,找目標變量和條件變量的轉(zhuǎn)化關(guān)系以及用設(shè)而不求、幾何和一些運算技巧進行合理運算.這堂課體現(xiàn)了數(shù)形結(jié)合、等價轉(zhuǎn)化、函數(shù)與方程、類比、特殊到一般思想等.

師:今天的作業(yè)：請同學們課后繼續(xù)自編幾個變式題進行深入探究.

教師提供另外樣例：

變式6變式3中去掉條件“線段AB被M平分”,求△PAB面積的最小值.

變式7變式5中加條件“PM⊥EF”,求點P的坐標.

變式8變式1中將“拋物線”改成“橢圓”,情況又怎樣？

設(shè)計意圖課堂教學的結(jié)束,并不意味著探究活動的結(jié)束.要求學生自編變式問題,將探究活動延伸到課外,培養(yǎng)學生主動探究數(shù)學問題的意識和習慣.

2 教學反思

2.1 相信學生,讓學生在合作探究中動起來

為了讓學生充分融入課堂,筆者決定課前不發(fā)學案,努力上一堂“原生態(tài)”的問題探究課.為了讓學生“動”起來,筆者在課堂上設(shè)計了2個平臺：其一,每一個問題都要讓學生積極參與,當一個學生給出解法或解題中斷后,鼓勵其他學生給出自己不同的解法或完善解法；其二,放手讓學生去改變問題的條件或結(jié)論進行變式探究,讓課堂多了些生成.如原來教學預設(shè)中沒有變式2(將點P一般化),但是學生提出來后,筆者及時調(diào)整了預設(shè),鼓勵學生進行探究,學生沿用通法解決問題,并得到一般性的結(jié)論.

實踐表明,“原生態(tài)”教學使得問題探究得更到位、更自然、更真實.如本課重點要突破的變式3、變式4的探究過程,學生能借助幾何直觀求解變式3.當有學生改變數(shù)據(jù)發(fā)現(xiàn)變式4時,教師能自然地引導學生先估計點的大致位置,同時用“幾何畫板”動畫演示,驗證學生的猜想,激發(fā)學生的學習熱情.有了形的直觀,再鼓勵學生進一步探究用數(shù)將直觀問題精確化,這不就是解析幾何所倡導的“以形助數(shù),以數(shù)解形”嗎?整節(jié)課都是由學生獨立思考或合作討論發(fā)現(xiàn)問題及解法,努力做到了讓課堂“動”起來.

由此筆者認為,在平時教學中,我們也要充分相信學生,在課堂中讓學生沉睡的思維被喚醒,創(chuàng)造的潛能被激發(fā).

2.2 變式探究,讓學生在合作探究中感受數(shù)學

著名的數(shù)學教育家波利亞曾說過：“好問題如同蘑菇,它們都成堆地生成,找到一個之后,你應當在周圍找一找,很可能附近就有好幾個.”高三復習課上應追求變式探究,讓學生在合作探究中感受數(shù)學.一方面在變中突出不變的解題方法,講一題、通一類、會一片,如本節(jié)課通過源問題的求解,讓學生回顧此類問題的2種通法(方法1、方法2),通過變式探究,使學生在解決變式1、變式2時,“重復”操練這2種求解方法,促進他們對數(shù)學技能的掌握,不斷提高分析問題、解決問題的能力；另一方面變式問題并非“生硬”的“外掛式”設(shè)置,不是生搬硬套地“拼湊”,而是要突出教學重點、突破教學難點,確保教學任務的順利完成，要符合學生的認知規(guī)律,有效引導并激活學生的數(shù)學思維，遞進要自然,以保證學生思維的連貫、通暢.

本節(jié)課對一類直線與拋物線的問題進行求解之后,思考：能否再引入條件(如圓)進行編題？因此有了變式3、變式4；從改變題型角度思考,從定點問題到定值、點坐標的求法、平分弦、最值等問題,有了變式5；最后繼續(xù)鼓勵學生將變式進行到底,教師提供另外樣例：變式6、變式7、變式8將探究活動延伸到課外.“變式探究”有利于擴大學生視野,深化知識,舉一反三,觸類旁通,從而增強學生分析問題、解決問題的自信心,激發(fā)他們的學習興趣.

2.3 滲透思想,讓學生在合作探究中打通解題思路

高考解析幾何大題屬于難題,特別是后半部分一般是尖子生拉開與其他考生距離的“分水嶺”.因此,解析幾何復習課要求例題教學中滲透數(shù)學思想,培養(yǎng)學生數(shù)學思維,逐步發(fā)展學生的能力.在分析問題、探索思路的過程中進行,用數(shù)學思想方法指導分析,讓學生去領(lǐng)悟隱含于例題的數(shù)學思想方法.

如本節(jié)課,當生1用韋達定理思維受阻而中斷解題時，教師設(shè)計了這樣幾個引導問題:“你要證明的結(jié)論(目標)是什么？能否將條件kAF=-kBF朝著你的目標去轉(zhuǎn)化呢？”等,幫助學生確定轉(zhuǎn)化的目標方向,并對條件轉(zhuǎn)化作出等價性分析.培養(yǎng)學生在解題過程中的目標意識、轉(zhuǎn)化能力及函數(shù)和方程的思想方法,并鼓勵學生自覺地運用學到的思想方法到后續(xù)的解題中去,最終達到用思想指導方法的思維習慣.在例題結(jié)束后進行提煉,加以顯化,讓學生回顧思維過程,總結(jié)運用了哪些數(shù)學思想方法.如本節(jié)課中,涉及到的數(shù)學思想有：特殊到一般、數(shù)形結(jié)合、設(shè)而不求等.

[1] 浙江省教育考試院.浙江省普通高考考試說明(文科)[M].杭州：浙江攝影出版社,2013:31.