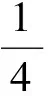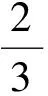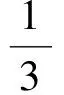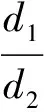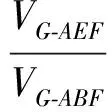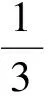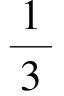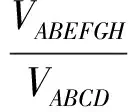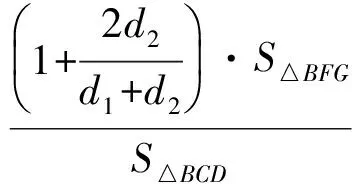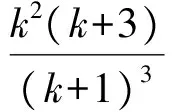自主招生中的立體幾何問(wèn)題
●
(松陽(yáng)縣第一中學(xué) 浙江松陽(yáng) 323400)
自主招生中的立體幾何問(wèn)題
●李玉梅
(松陽(yáng)縣第一中學(xué) 浙江松陽(yáng) 323400)
立體幾何試題是考查空間想象能力最好的載體.在自主招生試題中,這部分內(nèi)容主要考查空間圖形中線面的位置關(guān)系以及空間角、距離的計(jì)算,解題時(shí)往往將空間問(wèn)題轉(zhuǎn)化為平面問(wèn)題來(lái)解決,體現(xiàn)數(shù)學(xué)中的轉(zhuǎn)化與化歸思想.另外,建立空間直角坐標(biāo)系,將幾何元素之間的關(guān)系數(shù)量化,可以看出用空間向量來(lái)解題的優(yōu)勢(shì).本文主要談?wù)勛灾髡猩械牧Ⅲw幾何問(wèn)題.
1 求角的問(wèn)題
( )
(2011年清華大學(xué)等七校聯(lián)考試題)
評(píng)注本題也可以平移DM與AN共面,即點(diǎn)M移到點(diǎn)N,點(diǎn)D移到CD的中點(diǎn)Q,或平移AN與DM共面,亦即點(diǎn)A移到點(diǎn)M,點(diǎn)N移到PN的中點(diǎn)Q,平移是解決線線問(wèn)題的基本方法.
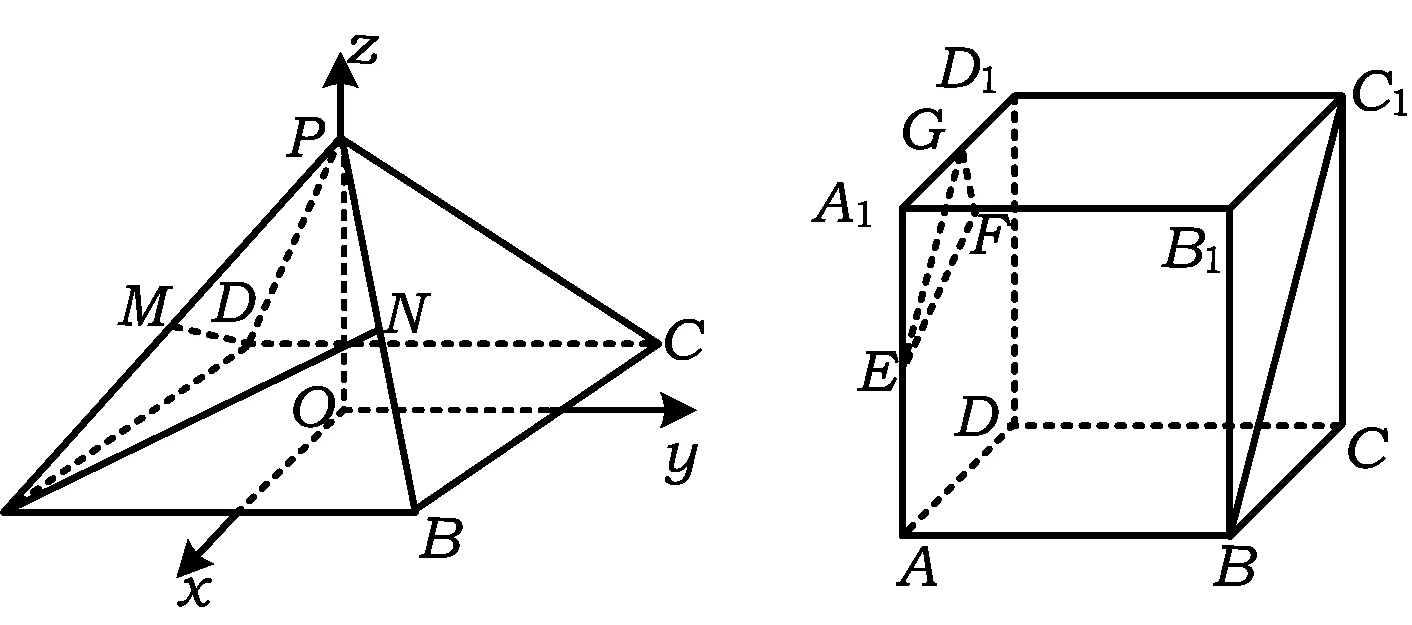
圖1 圖2
例2在正方體ABCD-A1B1C1D1中,E為棱AA1的中點(diǎn),F(xiàn)是棱A1B1上的點(diǎn),且A1F∶FB1=1∶3,則異面直線EF與BC1所成角的正弦值為
( )
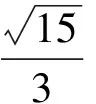
(2011年同濟(jì)大學(xué)等九校聯(lián)考試題)
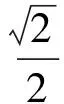
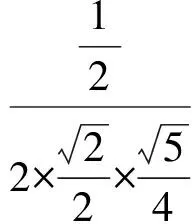
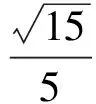
評(píng)注“線線角”問(wèn)題的常用方法是平移法,此題也可以用坐標(biāo)法求解.
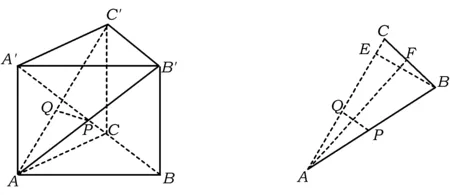
例3三棱柱ABC-A′B′C′的底面是邊長(zhǎng)為1的正三角形,高AA′=1,在AB上取一點(diǎn)P,設(shè)△PA′C′與底面的二面角為α,△PB′C′與底面的二面角為β,則tan(α+β)的最小值是
( )
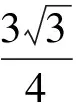
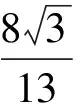
(2009年復(fù)旦大學(xué)自主招生試題)
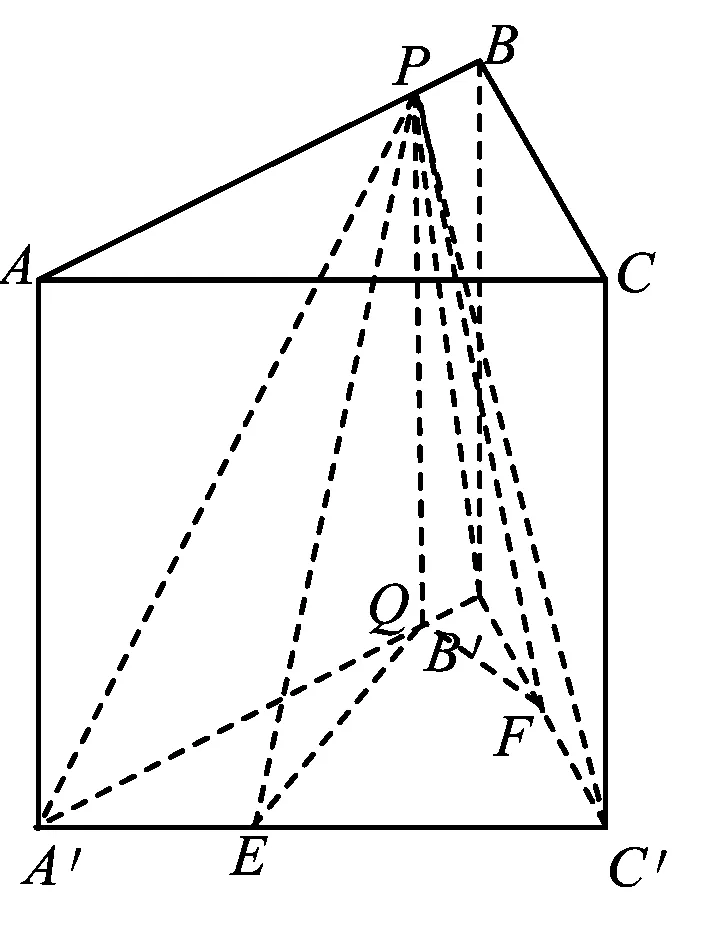
圖3
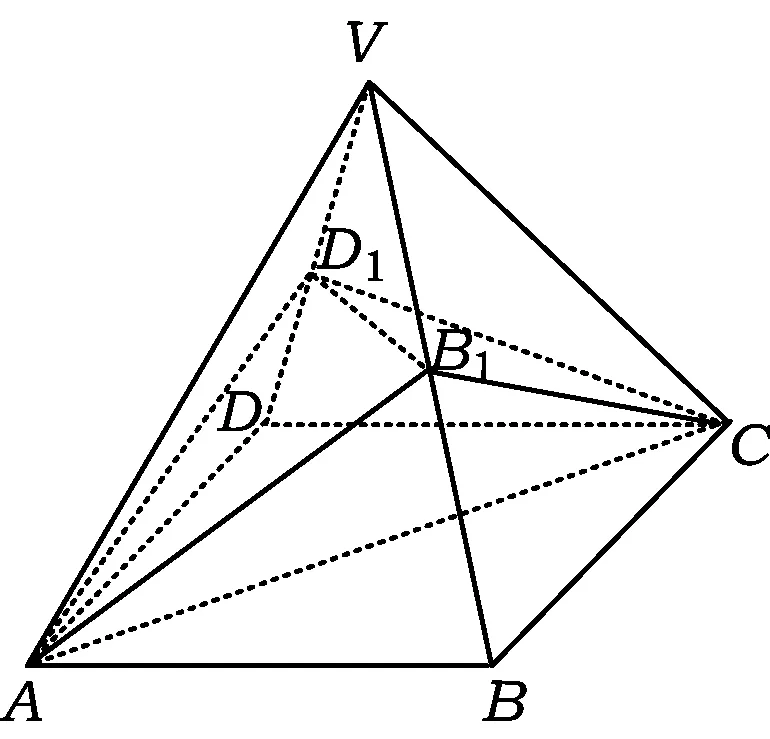
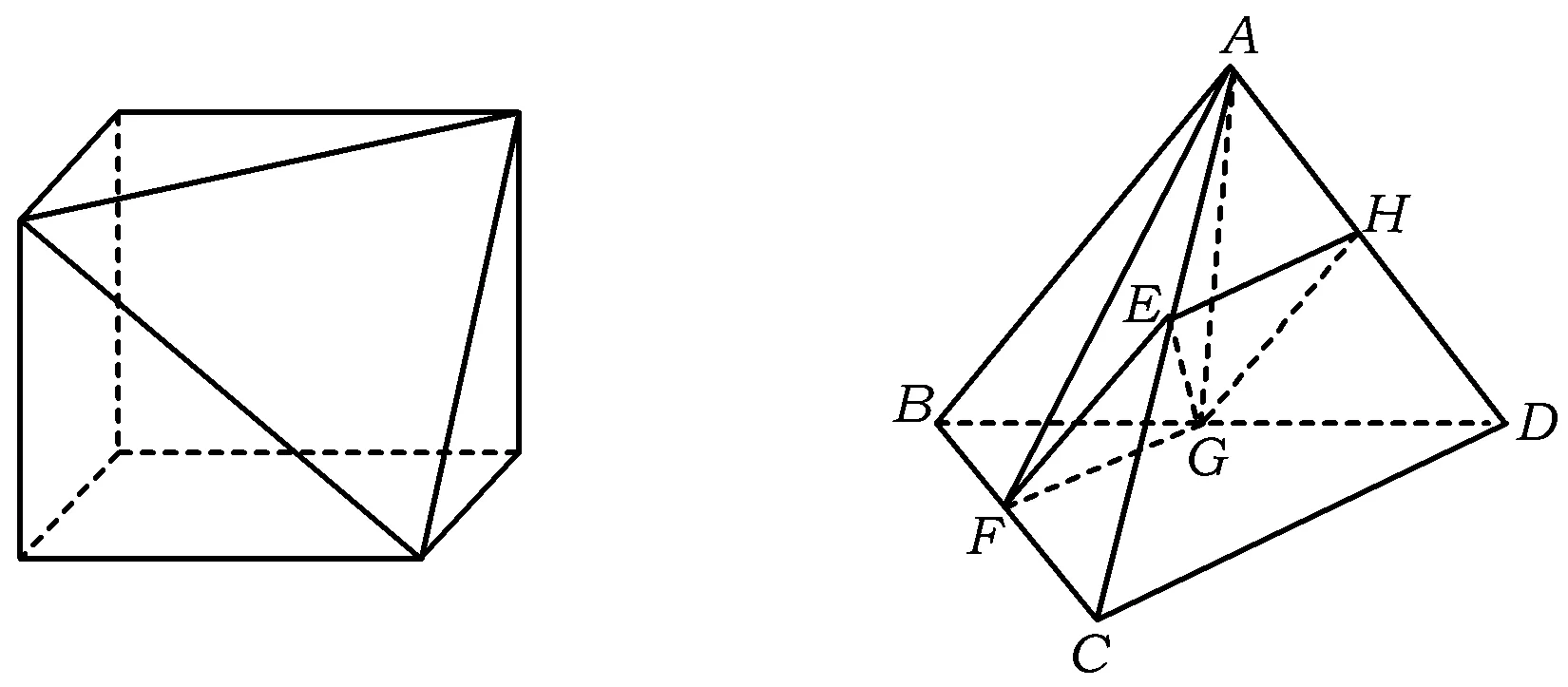
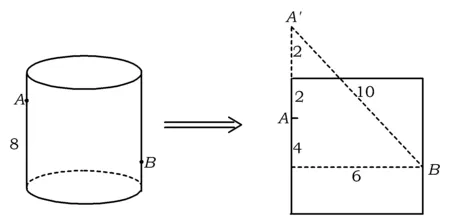
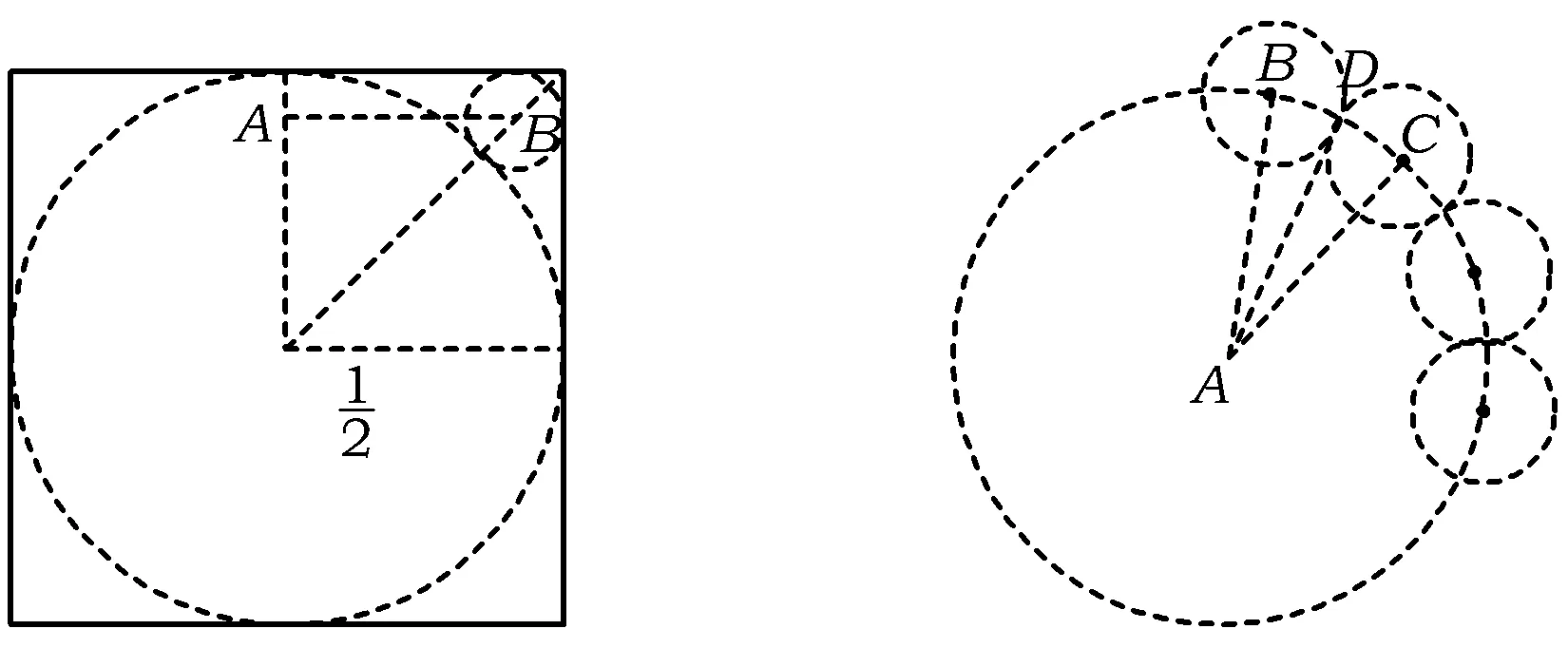
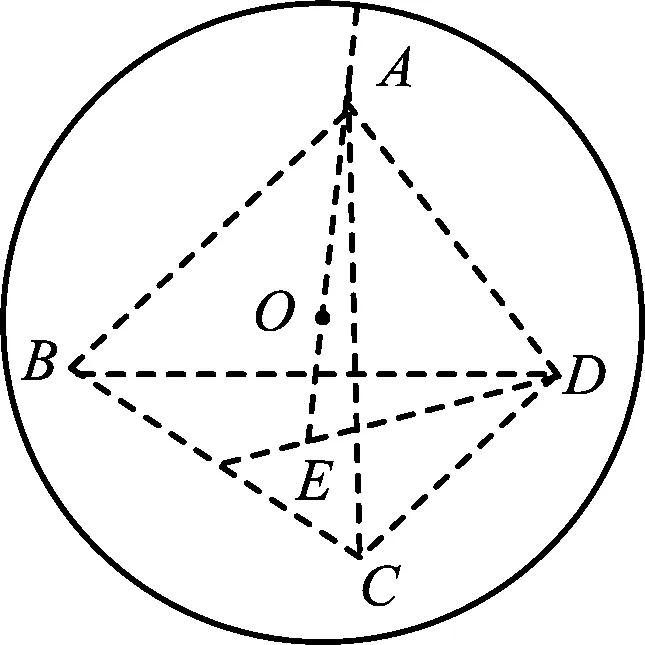
分析如圖3,Q為點(diǎn)P在平面AB′C′上的射影,作QE⊥A′C′,QF⊥B′C′,則∠PEQ,∠PFQ分別為二面角P-A′C′-B,P-B′C′-A′的平面角,即∠PEQ=α,∠PFQ=β.設(shè)B′Q=x,A′Q=1-x(0 從而 又 于是 評(píng)注求二面角的關(guān)鍵是根據(jù)已知條件準(zhǔn)確地找出或作出要求的角. 例4在三棱柱ABC-A1B1C1中,底面邊長(zhǎng)與側(cè)棱長(zhǎng)均等于2,且E為CC1的中點(diǎn),則點(diǎn)C1到平面AB1E的距離為 ( ) (2011年同濟(jì)大學(xué)等九校聯(lián)考試題) 分析本題每個(gè)選項(xiàng)中只有一個(gè)結(jié)果,因此滿足條件的任何一個(gè)三棱柱中所求距離為同一個(gè)數(shù)字.不妨取三棱柱ABC-A1B1C1為直三棱柱,如圖4所示,運(yùn)用等體積法,易求得點(diǎn)C1到平面AB1E的距離 故選D. 評(píng)注當(dāng)一般情況不易解決時(shí),要注意把問(wèn)題特殊化,如特殊數(shù)字、特殊函數(shù)、特殊圖像等,這樣可以使解題思路豁然開(kāi)朗. 例5設(shè)ABC-A′B′C′是正三棱柱,底面邊長(zhǎng)和高都為1,點(diǎn)P是側(cè)面ABB′A的中心,則點(diǎn)P到側(cè)面ACC′A′的對(duì)角線的距離是 ( ) 圖5 圖6 分析如圖5,作PQ⊥AC′,則PQ即為所求的距離.將△AB′C′分離出來(lái),作B′E∥PQ,交AC′于點(diǎn)E,取B′C′的中點(diǎn)F,聯(lián)結(jié)AF,如圖6.設(shè)PQ=h,則 評(píng)注空間的距離常轉(zhuǎn)化為平面的距離,而等面積法是求距離的常用方法之一. 例6有一個(gè)圓柱形杯子,底面周長(zhǎng)為12 cm,高為8 cm,點(diǎn)A在內(nèi)壁距杯口2 cm處,點(diǎn)A對(duì)面外壁距杯底2 cm處有一只小蟲(chóng),問(wèn)小蟲(chóng)至少走_(dá)_____cm長(zhǎng)的路才能到點(diǎn)A處飽餐一頓? (2009年南京大學(xué)自主招生試題) 分析根據(jù)題意可將圓柱形杯子展開(kāi),如圖7所示,小蟲(chóng)從點(diǎn)B到點(diǎn)A′的最短距離可利用勾股定理求得,即為10 cm. 評(píng)注幾何體的展開(kāi)是求最短距離的常用辦法之一. 圖7 ( ). A.32 B.30 C.28 D.26 (2010年復(fù)旦大學(xué)自主招生試題) 圖8 圖9 分析如圖8為過(guò)球心的截面圖,設(shè)小球的半徑為r,依題意有 解得 從而 所放入的小球如圖9所示的方式擺放,相鄰2個(gè)小球的球心B,C與圓心A構(gòu)成等腰三角形,點(diǎn)D為2個(gè)小球的切點(diǎn),則 從而 ∠CAB≈2×11.95°=23.9°<24°, 評(píng)注在解決立體幾何問(wèn)題時(shí),常會(huì)遇到若干個(gè)球按照一定的法則“疊加”的問(wèn)題,我們將這類問(wèn)題簡(jiǎn)稱為“多球”問(wèn)題.對(duì)于“多球”問(wèn)題,往往可以從多球中提煉出各球球心所組成的圖形,將問(wèn)題簡(jiǎn)化,然后通過(guò)解決該簡(jiǎn)化的問(wèn)題,獲得原問(wèn)題的待求結(jié)論,這是解決“多球”問(wèn)題的常用方法之一. 例8半徑為R的球內(nèi)部裝4個(gè)有相同半徑r的小球,則小球半徑r的最大值是 ( ) (2009年復(fù)旦大學(xué)自主招生試題) 圖10 因?yàn)?/p> AO=R-r, 所以 評(píng)注此題也是一個(gè)“多球”問(wèn)題,也可以從多球中提煉出各球球心所組成的立體圖形,將問(wèn)題簡(jiǎn)化. 例9一個(gè)球與正四面體的6條棱都相切,若正四面體的棱長(zhǎng)均為a,則這個(gè)球的體積為 ( ) 分析設(shè)正四面體為P-ABC,O為球心,R為球半徑,PO交底面ABC于點(diǎn)D,則點(diǎn)D是△ABC的重心.聯(lián)結(jié)AD,作DE⊥AB于點(diǎn)E,聯(lián)結(jié)OE.在Rt△ODE中, 在Rt△PAD中, 從而 評(píng)注球的內(nèi)接外切問(wèn)題的關(guān)鍵是分析幾何體的特征,根據(jù)條件求出球的半徑. 例10在四棱錐V-ABCD中,B1,D1分別為側(cè)棱VB,VD的中點(diǎn),則四面體AB1CD1的體積與四棱錐V-ABCD的體積之比為 ( ) A.1∶6 B.1∶5 C.1∶4 D.1∶3 圖11 評(píng)注體積問(wèn)題常常利用“等(同)底等(同)高的體(面)積相等”來(lái)求解. 例11設(shè)一個(gè)多面體從前面、后面、左面、右面、上面看到的圖形分別如圖12所示,則該多面體的體積為 ( ) (2010年復(fù)旦大學(xué)自主招生試題) 圖12 解聯(lián)想由正方體變化得到的幾何體,如圖13所示,其圖形即為正方體去掉“一個(gè)角”,則 圖13 圖14 分析設(shè)點(diǎn)A到平面DBC的距離為h.在△ABC中,因?yàn)锳E∶EC=d1∶d2,所以 從而 又因?yàn)?/p> VG-AEF=VG-AEH, 評(píng)注體積問(wèn)題是立體幾何中的重要問(wèn)題.在高中數(shù)學(xué)競(jìng)賽與自主招生試題中,利用體積法解題形式簡(jiǎn)潔,構(gòu)思容易,內(nèi)涵深刻,應(yīng)用廣泛,備受青睞.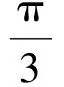
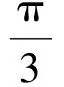
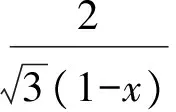
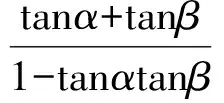
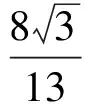
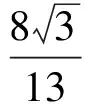
2 距離問(wèn)題
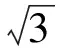
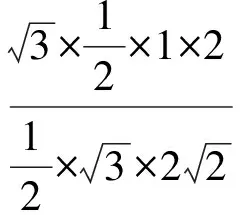

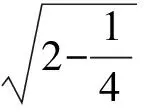

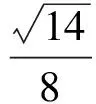
3 內(nèi)接外切問(wèn)題


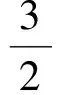

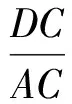

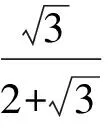
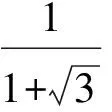
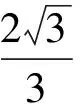
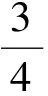
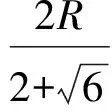
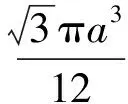
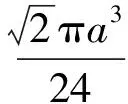
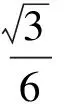
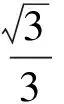
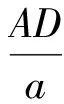
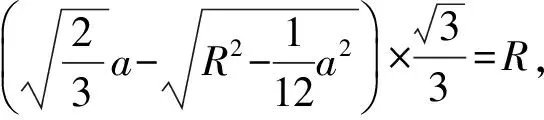
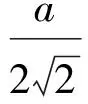
4 體積問(wèn)題