試題中數學文化的考查舉例
——以2013年福建省高三數學質檢卷為例

●

(泉州市第五中學 福建泉州 362000)

試題中數學文化的考查舉例
——以2013年福建省高三數學質檢卷為例

●楊蒼洲

(泉州市第五中學 福建泉州 362000)

《普通高中數學課程標準》在“課程基本理念”中指出：“數學是人類文化的重要組成部分.數學課程應反映數學的歷史、應用和發展趨勢，數學對推動社會發展的作用，數學的社會需求，社會發展對數學發展的推動作用，數學科學的思想體系，數學的美學價值，數學家的創新精神.數學課程應幫助學生了解數學在人類文明發展中的作用，逐步形成正確的數學觀.為此，高中數學課程提倡體現數學的文化價值，并在適當的內容中提出對數學文化的學習要求.”時至今日，課程改革正往縱深的方向推進，走至深處，“文化”才是課程的核心.因此，如何在試題中對數學文化進行考查，以發揮考試指揮棒的作用是命題工作者應該思考的重要問題.

湖北省的高考命題在對數學文化的考查方面作出了很大的努力,如：2009年湖北省文、理科的第10題均以“古希臘人研究的三角形數、正方形數”為背景，理科第15題以“角谷猜想”為背景；2011年湖北省文科第9題、理科第13題以《九章算術》的“竹九節問題”為背景，理科第15題以“斐波那契數列”為背景；2012年湖北省文科第17題以“古希臘畢達哥拉斯學派的三角形數”為背景，理科第10題以《九章算術》中“開立圓術”為背景，理科第13題以“回文數”為背景.

上述大部分試題是以數學史為背景進行命制的.那么，考查數學文化的試題是否也只能以數學史、數學故事為背景進行命制呢？數學文化是否等同于數學史呢？回答是否定的！數學文化并不只是簡單的數學史、數學故事、趣味數學，把數學文化等同于數學史的認識是淺薄的、狹隘的.隨著數學學科的發生、發展，伴隨著數學知識的發生、發展、傳播而積蓄下的數學思維方式、數學思想觀念及數學精神品格等，這些都屬于數學文化.文獻[2]把數學文化的內涵概括為：(1)數學的歷史；(2)數學的思想；(3)數學的精神；(4)數學與人類其他知識領域之間的關聯.下面筆者從這4個角度對2013年福建省高三數學質檢卷的個別試題進行剖析，談談如何在試題命制中滲透數學文化的考查.

1 滲透數學歷史的考查——在故事中得到啟迪

數學的歷史是數學文化的一部分，這是無可爭議的.在數學史中尋找命題背景也一直被命題者所推崇.如果說近幾年湖北省的試題隱含著對數學歷史的考查，那么下述試題對數學歷史的考查則更是深藏不露.

( )

A．5nB．10n

C．5(n+1) D．10(n+1)

例1以平面向量的運算為載體，考查平面向量的加法運算、平面向量的模長、數列求和等基礎知識，考查運算求解能力、應用意識、創新意識；考查化歸與轉化思想、數形結合思想.本題貌似與“數學歷史”毫無關聯，實則不然，問題速解的思路當來源于我們耳熟能詳的“高斯的故事”，即高斯利用“倒序求和”的方法計算“1+2+…+100”.考生若能對“倒序求和”的方法進行遷移應用就能實現對本題的巧解.這種數學史的隱性考查，對考生的應用遷移能力提出了較高的要求.

2 滲透數學思想的考查——在過程中感受思想

過程比結果更重要.若干年后，大部分學生將不再學習數學，當這部分學生不再進行繁雜的數學運算時，數學教學能為他們留下的只有“思想”了，因此，數學思想就是數學文化的重要組成部分.下述試題將為我們展示如何對知識發生、發展過程中所蘊含的數學思想方法進行考查.

例2如圖1，A1,A2,…,Am-1(m≥2)為區間[0,1]上的m等分點，直線x=0，x=1，y=0和曲線y=ex所圍成的區域為Ω1，圖中m個矩形構成的陰影區域為Ω2，在Ω1中任取一點，則該點取自Ω2的概率為______．

例2以“定積分概念形成過程所蘊含的思想——以直代曲”為載體，考查等比數列的前n項求和公式、定積分的概念、幾何概型等基礎知識；考查運算求解能力、創新意識；考查化歸與轉化思想、數形結合思想、有限與無限思想.張奠宙教授在文獻[3]中談論了高中文科生學習微積分的意義：“微積分在他們的腦海里，已經跨越初等數學靜態的、孤立的思維模式，能用局部與整體的哲學思維動態地進行思考，理解微積分對人類的偉大貢獻.這種思考能力，正是現代公民所需要的一種數學文化素質.”本題努力將高中數學教學導向于關注過程、感受思想.

3 滲透數學應用的考查——在生活中實踐應用

人教A版高中數學課標教材主編劉紹學先生在主編寄語中說：“數學是有用的、數學是自然的.”如何應用所學數學知識分析和解決生產、生活中的數學問題是學習數學的意義所在.因此，學以致用是數學教學的目標之一，數學應用是數學文化的又一重要組成部分.

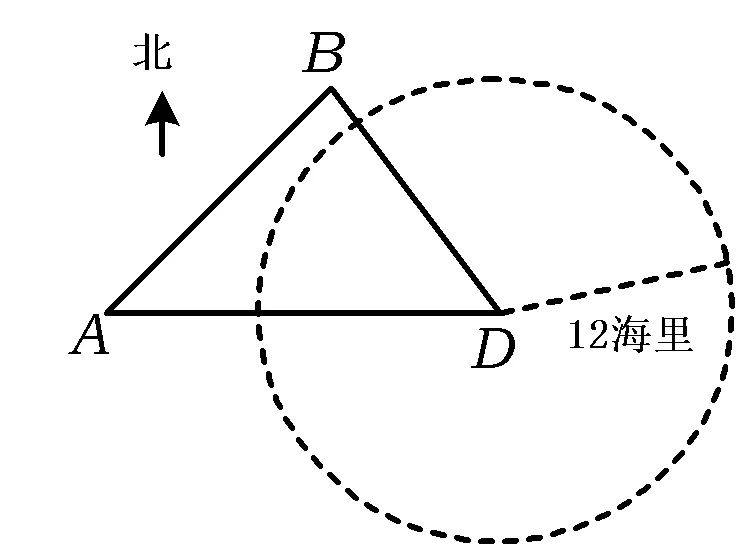
圖2

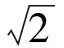
(1)求此時該外國船只與島D的距離.

(2)觀測中發現，此外國船只正以每小時4海里的速度沿正南方向航行.為了將該船攔截在離島D的12海里處，不讓其進入島D的12海里內海域，試確定海監船的航向，并求其速度的最小值(參考數據：sin36°52′≈0.6,sin53°08′≈0.8).

例3以“海監船維權巡航”為背景，考查余弦定理等基礎知識，考查應用意識、運算求解能力，考查化歸與轉化思想等.“發展學生的數學應用意識”是課標課程的理念之一，同時，課標提出應力求使學生體驗數學在解決實際問題中的作用、數學與日常生活及其他學科的聯系，促進學生逐步形成和發展數學應用意識，提高實踐能力.因此，應用題是考查數學文化的一傳統陣地.

4 滲透數學精神的考查——在理性中得以確認

克萊因把數學看成是“一種精神，一種理性精神”，齊民友先生則進一步認為數學精神集中地體現為“徹底的理性探索精神”.當前數學教學往往只是關注數學在知識層面上的應用，而忽視數學精神的教育功能.對數學文化中的理性精神，齊民友先生作出了精辟的論述：“每個論點都必須有根據，都必須持之以理，除了邏輯要求和實踐檢驗外，無論是幾千年的習俗、宗教的權威、皇帝的敕令，還是流行的風尚統統是沒有用的.”

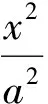
(1)求橢圓E的方程.

(2)給出命題：“已知P是橢圓E上異于A1,A2的一點，直線A1P,A2P分別交直線l：x=t(t為常數)于2個不同的點M,N，點Q在直線l上.若直線PQ與橢圓E有且只有一個公共點P，則點Q為線段MN的中點”，寫出此命題的逆命題，判斷你所寫出命題的真假，并加以證明.

(3)試研究第(2)小題的結論，根據你的研究心得，在圖4中作出與該雙曲線有且只有一個公共點S的直線m，并寫出作圖步驟(注意：所作的直線不能與雙曲線的漸近線平行).

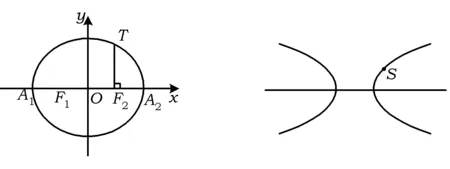
圖3 圖4

例4主要考查橢圓的標準方程與性質、直線與圓錐曲線的位置關系等基礎知識；考查推理論證能力、運算求解能力；考查化歸與轉化思想、數形結合思想、特殊與一般思想等．“直觀感知、演繹證明、操作確認”是數學認識的不同階段，在第(3)小題中，學生首先要能夠從橢圓到雙曲線進行正確的類比遷移，從而得到“直觀感知”.理性精神是堅持以理性或以理性為基礎的思維方法作為判斷真假、是非的標準.因此，考生必須研究第(2)小題的結論及其證明過程，同時進行類比推理，雖然這里不需表達出證明的過程，但是考生需要“演繹證明”該心理過程，最后通過動手作圖實現“操作確認”，這是一個從感性認識到理性認識的過程.因此，通過本題將引導我們重新審視數學精神的教育價值.

5 與其他關聯知識的考查——在交匯中拓寬視野

《考試大綱》明確提出“從學科的整體高度和思維價值的高度考慮問題，在知識網絡交匯點設計試題，使對數學基礎知識的考查達到必要的深度”的考查要求.知識的交匯大致可以分為學科內的知識交匯和跨學科的知識交匯，學科內的知識交匯能高效地檢測學生的基礎知識和基本技能，跨學科的知識交匯能有效而全面地檢測考生的整體數學素養.因此，在交匯點處設置試題，特別地，在“數學與人類其他知識領域之間的關聯”處進行交匯，是考查數學文化的一種有效手段.

圖5

例5如圖5，某學生用“幾何畫板”研究拋物線的性質：打開幾何畫板軟件，繪制拋物線E:y2=2px，在拋物線上任意畫一個點S，度量點S的坐標為(xs,ys)．

(1)拖動點S，發現當xS=4時，yS=4，試求拋物線E的方程.

(2)設拋物線E的頂點為A，焦點為F，構造直線SF交拋物線E于2個不同的點S,T，構造直線AS,AT分別交準線于點M,N，構造直線MT,NS．經觀察得：沿著拋物線E，無論怎樣拖動點S，恒有MT∥NS.請你證明這一結論．

(3)為進一步研究該拋物線E的性質，某學生進行了下面的嘗試：在第(2)小題中，把“焦點F”改變為其他“定點G(g,0)(g≠0)”，其余條件不變，發現“MT與NS不再平行”．是否可以適當更改第(2)小題中的其他條件，使得仍有“MT∥NS”成立？如果可以，請寫出相應的正確命題；否則，說明理由．

例5以“運用幾何畫板探究拋物線性質”為載體，主要考查拋物線的標準方程、直線與圓錐曲線的位置關系、合情推理等基礎知識；考查推理論證能力、運算求解能力；考查化歸與轉化思想、分類與整合思想、數形結合思想等．體現了在知識的交匯點處命題的指導思想，同時也倡導“注重信息技術與數學課程的整合”的課程理念.

6 結束語

《普通高中數學課程標準》關于課程目標的具體目標之一：“具有一定的數學視野，逐步認識數學的科學價值、應用價值和文化價值，形成批判性的思維習慣，崇尚數學的理性精神，體會數學的美學意義，從而進一步樹立辯證唯物主義和歷史唯物主義世界觀.”

誠然，數學的推理方法、研究方法、思維方式、理性精神等這些都將使一個數學學習者終身受益.數學文化滲透于教學過程已成為數學課程的目標，因此，如何將數學文化自然地滲透于數學試題，將是一個重要的課題.

[1] 中華人民共和國教育部制定.普通高中數學課程標準(實驗)[M].北京：人民教育出版社,2003:2-3.

[2] 趙東霞，汪曉勤.關于數學文化教育價值與運用現狀的網上調查[J].中學數學月刊，2013(3)：41-44.

[3] 張奠宙.《普通高中數學課程標準》的回顧與展望[J].中學數學月刊，2013(3)：1-3.