“算兩次”在自主招生解題中的應用

●

(嘉興市第一中學 浙江嘉興 314050)

“算兩次”在自主招生解題中的應用

●沈曉飛呂峰波

(嘉興市第一中學 浙江嘉興 314050)

近幾年自主招生的地位及權重逐漸提升，越來越受到師生的重視．由于自主招生實施的主體是高校，教育理念與高中有所不同，其命題風格及試題特點與高考也有一定的差異．作為優秀人才選拔模式的新探索，各高校的自主招生數學試題相對于高考數學試題而言，更加關注數學思維品質，強調數學學科和思想方法的考查．

筆者通過研究近幾年的自主招生試題，發現“算兩次”在自主招生解題中有著廣泛應用．“算兩次”又稱富比尼原理，是指對同一對象從2種不同的角度去分析研究，從而找到解決問題的途徑．在實際解題中，往往可以就線段的長度、數值的大小、模型的種數、函數的最值、事件的概率等“算兩次”．

1 算線段的長度

例1如圖1，用2個鋼珠測算一工件的圓柱體內直徑d，若半徑為r1的鋼珠上端與孔口平面距離為h1，半徑為r2的鋼珠上端與孔口平面距離為h2，則內直徑d=______．

(2010年上海交通大學自主招生試題)

圖1 圖2

分析如圖2，設O1E=x.因為AB=CD，所以

2r2+h2=r2+x+r1+h1，

即

x=r2-r1+h2-h1，

于是

故內直徑

評注美國數學教育家波利亞說：為了得到一個方程，我們必須把同一個量以2種不同的方法表示出來，即將一個量“算兩次”，從而建立相等關系.本題抓住圓柱體的高，利用AB=CD“算兩次”，求出關鍵量O1E，從而使問題得到解決．

圖3

例2在圓內接四邊形ABCD中，AB=1，BC=2，CD=3，DA=4，求四邊形ABCD的外接圓半徑．

(2009年北京大學自主招生試題)

分析如圖3，聯結BD，設∠BAD=θ，則∠BCD=π-θ，設四邊形ABCD的外接圓半徑為R．在△ABD中，由余弦定理知

BD2=AB2+AD2-2AB·ADcosθ=17-8cosθ;

(1)

在△BCD中，由余弦定理知

BD2=BC2+CD2-2BC·CDcos(π-θ)=13+12cosθ.

(2)

評注在△ABD和△BCD中分別計算BD，得到關于cosθ的方程，進而求出R．在實際解題中也可以就角的計算“算兩次”．

2 算數值的大小

例3有個2 013×2 013的正方形數表，每行都成等差數列，每列各數平方后成等差數列．求證：左上角實數×右下角實數=左下角實數×右上角實數．

(2013年北京大學保送生試題)

證明記數表(如表1所示)左上角、右上角、左下角、右下角4個數分別為a,b,c,d，設最中間那個數為x．

表1 2 013×2 013的正方形數表

兩邊平方并化簡，得ad=bc．若兩者都取負號或者一正一負，同理可得ad=bc．

評注本題利用“中心開花”的思想，抓住表格中心的數值，分別從行和列2個不同的角度“算兩次”，得到了所要求證的關系式．

3 算模型的種數

(2006年復旦大學自主招生試題)

(1+x)2n=(1+x)n(1+x)n=

展開后xn的系數是

解法2“魚目混珠”問題.

例5對正六邊形的邊和所有對角線染色，任意三角形3條邊染色不同，任意2組三角形染色方式不同，求至少要染多少種顏色？

(2010年清華大學等五校聯考試題)

圖4

另一方面，當n=7時，構造這樣一種染色方案．記7種顏色為0，1，2，…，6．記六邊形ABCDEF的6個端點對應數字1，2，…，6，按照這樣的規則染色：每一條邊染的顏色編號和該邊2個端點對應數字之和相同(在模7下運算)，如：EF的2個端點編號之和為11，模7后為4，則染顏色4，以此類推.

在這樣的染色方案下，若有2個三角形的染色方案完全相同，設2個三角形對應的頂點編號分別為a,b,c,a′,b′,c′.不妨設

a+b≡a′+b′(mod7)，

a+c≡a′+c′(mod7)，

b+c≡b′+c′(mod7),

則

2(a+b+c)≡2(a′+b′+c′)(mod7),

即

a+b+c≡a′+b′+c′(mod7),

從而a≡a′(mod7)，b≡b′(mod7)，c≡c′(mod7)，

故

a=a′，b=b′，c=c′.

即這2個三角形為同一個三角形，矛盾.因此,任何2個三角形的染色搭配都不一樣.綜上所述，最少染7種顏色即可．

評注本題即求證nmin=7．從2方面進行論證：(1)n≥6且n=6不滿足條件，這說明nmin≥7；(2)構造了n=7時滿足條件的例子，這說明nmin≤7．由(1)和(2)可知nmin=7．這種“算兩次”的方法在求函數的最值時也經常用到．

4 算函數的最值

例6已知對任意x∈R，acosx+bcos2x≥-1恒成立，求(a+b)max．

(2009年北京大學自主招生試題)

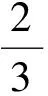
因此

a+b≤2．

恒成立．

綜上所述，(a+b)max=2．

評注在本題中，若令t=cosx，則不等式轉化為2bt2+at-b+1≥0，可以根據二次函數性質來分類討論．這里用“算兩次”的方法有效地回避了分類討論，將其置于一般函數的知識背景下，在抓住本質的同時，使解答簡潔、明快．

例7有100個容納量相同的箱子，每個箱子內裝2件貨物，共200件．在取出來的過程中貨物順序打亂了，現要按一定的順序將貨物依次再裝入箱子中，每個箱子最多裝2件貨物．若某貨物能裝入該箱子，則裝入；若不能，則裝入下一個箱子(如貨物順序為0.7，0.5，0.5，0.3，則第1個箱子到面前時放入0.7的貨物，放不進0.5的貨物，0.5放入下一個箱子，另一個0.5也放入該箱子，0.3放入第3個箱子，這樣共需要3個箱子)．求最壞的情況下需要幾個箱子．

(2010年清華大學自主招生試題)

分析一方面，這200件物品無論怎樣擺放，一定可以將某2個相鄰物品放入同一個箱子，否則記這200件物品質量為ai(1≤i≤200)，且箱子容納量為M．不妨設隨意擺放依次為a1,a2,…,a200，且

a1+a2>M,a3+a4>M,…,a199+a200>M，

相加得100M>100M，矛盾！

另一方面，構造一種情況說明198個箱子不能裝下這200件物品．設

ai=100+(i-1)×0.01(1≤i≤200)，

且這200件物品依次擺放為a200,a3,a199,a4,a198,a5,a197,…,a103,a100,a102,a101,a2,a1,此時箱子容納量M=201.99．可以驗證，上述擺法只有重量為a101和a2的2個物品能放入同一個箱子，其余的每個物品都只能放在一個箱子中．

綜上所述，至少需要199個箱子才能確保裝下這200件物品，即最壞需要199個箱子．

評注需要的箱子數m相當于是這200件物品質量的多元函數，問題即求mmin．198個箱子不能放入說明mmin≥199，199個箱子能裝入，說明mmin≤199．

5 算事件的概率

例812個人圍坐在一個圓桌旁參加一個游戲，主持人給每人發一頂帽子，帽子的顏色包括紅、黃、藍、紫4種顏色．每個人都可以看見所有其他11個人帽子的顏色，但是不知道自己帽子的顏色．現在主持人讓這12個人順次來猜自己頭上帽子的顏色．這12個人可以事先約定好一種策略，但是當游戲開始后不能進行交流，他們的目標是使12個人同時回答正確的機會最大．假定主持人給每個人發帽子的顏色是完全隨機的，試給出一種策略，并分析在此策略下所有人都猜對的概率．

(2010年清華大學自主招生試題)

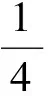
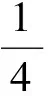
“算兩次”從操作層面上來說要根據問題所給的題設條件選擇一個適當的量，將其置于2種不同的知識、方法背景下分別考慮，然后通過所選取的適當量架起彼此間聯系的橋梁來解決問題，其中可能涉及到“構造”的成分，除本文所涉及到的幾個角度外，讀者還可以從點、元素、交點、對子、子集等方面作進一步研究和探索．“算兩次”從解題形式來說一般是這樣的：一方面……;另一方面……;綜合起來可以得到……．通過“算兩次”來解決問題能有效地培養學生思維的發散性、形成創新意識、使學生體會到數學知識的內在聯系及統一性．