當“偶然”邂逅“必然”
——圓錐曲線的一個優美性質

●

(溫州中學 浙江溫州 325014)

當“偶然”邂逅“必然”
——圓錐曲線的一個優美性質

●林慶望

(溫州中學 浙江溫州 325014)

1 問題的提出

筆者提供給學生的訓練題中，有這樣一道填空題：

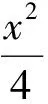
本題看起來很簡潔，但做起來并不容易.在上課分析該題時，筆者抽取了幾個學生，詢問了他們求解此題的思路，學生幾乎都用特殊法，即：

當點A為橢圓右焦點時，根據橢圓對稱性，得|FN|=|MA|.由橢圓定義可知，

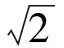
2 問題的延伸

很多數學問題往往在特殊數字中蘊含著一般規律，這在解析幾何中顯得尤其突出.

解設FA的中點坐標為(x0,0)，M(x1,y1),N(x2,y2),則圓的方程為

(x-x0)2+y2=(x0+c)2.

與橢圓方程聯立方程組

得

由橢圓的焦半徑公式可得

|FM|+|FN|= (ex1+a)+(ex2+a)=

而

|FA|=2x0+2c,

因此

于是得到一個優美的性質：

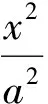
這時候學生終于如釋重負，露出舒心的笑容.此時又有學生提出了新的想法：在雙曲線和拋物線中是否也有這樣結論呢？這種類比的思想很合理.課后筆者還是繼續剛才的思考，得出更一般的結論和更簡潔的證明.

3 問題的解決

圖1 圖2 圖3

證明(以橢圓為例)以焦點F為極點，建立極坐標系.記|FA|=d，M(ρ1,θ1)N(ρ2,θ2)分別是橢圓與圓的公共點，于是

即

decos2θ-dcosθ+ep=0，

從而

又因為在圓中△FMA與△FNA都是直角三角形,所以

因此

4 感悟

數學教育家波利亞曾說過：“好問題同蘑菇類似，它們都成堆地生長，找到一個以后，你應當在周圍找一找，很可能附近就有好幾個.”在平時課堂教學中，意外的生成往往是不可多得的教學素材，教師千萬不可錯過這個探究知識的契機，幫助學生挖掘出更多的“蘑菇”.教師不僅要和學生一起找到問題的答案，更要讓學生知道問題的一般規律即數學本質.正確認識必然性與偶然性的辯證關系對學習和研究數學有重要的指導意義，特別在新課改理念指引下，教師要培養學生透過大量偶然性的表面現象去揭示其中蘊含的一般規律，由現象認識本質，由個別到一般，由經驗上升為理論，這一點在新課改中顯得尤其重要.