問題鏈驅(qū)動(dòng)下的探究式教學(xué)
——“任意角的概念”教學(xué)設(shè)計(jì)評(píng)析

●

(小海中學(xué) 江蘇南通 226015)

問題鏈驅(qū)動(dòng)下的探究式教學(xué)
——“任意角的概念”教學(xué)設(shè)計(jì)評(píng)析

●黃鋒

(小海中學(xué) 江蘇南通 226015)

三角函數(shù)是描述周期現(xiàn)象的重要數(shù)學(xué)模型，三角函數(shù)一章的研究，從具體問題入手，以問題為背景，體現(xiàn)了“問題情景―建立模型―解釋、應(yīng)用與拓展”的過程．“任意角”是三角函數(shù)的第一課，是在銳角、直角、鈍角，平角、周角的基礎(chǔ)上，對角的概念進(jìn)一步推廣.本節(jié)課需要解決好以下幾個(gè)問題：首先是推廣角概念的必要性；其次是正角、負(fù)角、零角、象限角、軸線角以及終邊相同的角等概念建構(gòu)的自然性、合理性；再次是對終邊相同角的集合的表示及判斷象限角等知識(shí)運(yùn)用環(huán)節(jié)中難點(diǎn)處理的巧妙性．理解任意角的概念，會(huì)在平面內(nèi)建立適當(dāng)?shù)淖鴺?biāo)系，通過數(shù)形結(jié)合來認(rèn)識(shí)角的幾何表示和終邊相同角的表示，是學(xué)好本課的關(guān)鍵．

為了調(diào)動(dòng)學(xué)生的學(xué)習(xí)興趣，本節(jié)課從學(xué)生熟悉的生活情境入手.為了使學(xué)生能夠輕松地理解看似零碎的概念，本節(jié)課借助類比，引導(dǎo)學(xué)生觀察、思考并感悟概念的本質(zhì).為了使學(xué)生深刻理解難點(diǎn)，本節(jié)課借助生活中的時(shí)鐘模型，通過設(shè)疑來激發(fā)學(xué)生的思維，通過學(xué)生自己動(dòng)手、體會(huì)、歸納，從而解決難點(diǎn)．整節(jié)課以問題鏈的形式展開，通過層層設(shè)問，引導(dǎo)學(xué)生自主發(fā)現(xiàn)問題，自主解決問題；學(xué)生探究性學(xué)習(xí)活動(dòng)貫穿于整個(gè)解決問題的始終.本文主要從3個(gè)方面結(jié)合教學(xué)設(shè)計(jì)來談?wù)劰P者對“任意角的概念”教學(xué)實(shí)施過程中的一些認(rèn)識(shí).

1 優(yōu)化數(shù)學(xué)情境，自然引出課題

課堂教學(xué)中，教師有目的、有意識(shí)地引入或創(chuàng)設(shè)具有一定情緒色彩、以形象為主體的、生動(dòng)具體的情境，可以使所有的學(xué)生都參與到數(shù)學(xué)學(xué)習(xí)中來，激發(fā)每一個(gè)學(xué)生的學(xué)習(xí)熱情和學(xué)習(xí)興趣，幫助學(xué)生更好地理解教材.本課教學(xué)安排了學(xué)生非常熟悉的摩天輪的例子，具體內(nèi)容如下：

情境游樂園是人們愛去的地方，各種神奇的游戲器械吸引著人們?nèi)ネ嫠＃叽蟮哪μ燧喞@軸轉(zhuǎn)動(dòng)著，邊緣上懸掛的座椅，帶著游人在空中旋轉(zhuǎn)，給游人帶來樂趣！星期天小明的父母帶小明到游樂園玩，父母讓小明獨(dú)自一人乘坐摩天輪(摩天輪20分鐘轉(zhuǎn)一圈)，而父母分別站在摩天輪的2側(cè).

問題1小明坐上最底部的一個(gè)座椅，第5分鐘時(shí)，摩天輪轉(zhuǎn)動(dòng)多少角度？第10分鐘呢？第1次回到起點(diǎn)時(shí)呢？第2次回到起點(diǎn)時(shí)呢？

問題2720°是怎樣的一個(gè)角呢?

問題3小明的父母看到摩天輪轉(zhuǎn)動(dòng)的方向一致嗎？

問題4在實(shí)數(shù)中，具有相反意義的量是如何表示的？

問題5在旋轉(zhuǎn)形成的角中，如何刻畫具有相反意義的角呢？

設(shè)計(jì)意圖問題1為了引出學(xué)生熟悉的直角、平角、周角以及720°角，其中720°角已經(jīng)超出了0°～360°的范圍.問題2起著回顧小學(xué)、初中角的定義的作用，引導(dǎo)學(xué)生從“靜態(tài)”和“動(dòng)態(tài)”2個(gè)角度思考，重點(diǎn)落在本質(zhì)“轉(zhuǎn)”上，為后續(xù)學(xué)習(xí)作鋪墊.問題3幫助學(xué)生體會(huì)到：考慮旋轉(zhuǎn)所成的角還應(yīng)考慮方向.通過上述問題可使學(xué)生感悟到角的概念有必要做進(jìn)一步的推廣(板書課題).問題4和問題5引導(dǎo)學(xué)生類比正、負(fù)數(shù)，從而將角的概念推廣到任意角，即正角、負(fù)角和零角.

2 巧設(shè)數(shù)學(xué)問題，合理展開探究

新課程倡導(dǎo)教師開展探究性教學(xué)，鼓勵(lì)學(xué)生自主參與學(xué)習(xí)活動(dòng)，通過親身體驗(yàn)，不斷質(zhì)疑，逐步形成勤于動(dòng)手、樂于探究、努力求知的積極態(tài)度.數(shù)學(xué)的探究性活動(dòng)，往往是圍繞一個(gè)實(shí)際問題展開.為了能夠有效地開展探究性教學(xué)活動(dòng)，本課圍繞教學(xué)主線，輔助問題鏈，引導(dǎo)和鼓勵(lì)學(xué)生自主發(fā)現(xiàn)問題，自主地探究，設(shè)計(jì)解決問題的方案，從而自主解決問題.主體教學(xué)過程如下：

2.1 巧妙設(shè)計(jì)教學(xué)思路，提煉課堂的教學(xué)主線

教學(xué)主線:情境→概念→模型→建構(gòu)→應(yīng)用→類比理解→拓展.

2.2 巧妙利用生活經(jīng)驗(yàn)，激發(fā)學(xué)生的參與熱情

(1)請學(xué)生們說說，生活中還有哪些與角的旋轉(zhuǎn)相關(guān)的實(shí)例？

(2)以學(xué)生們非常熟悉的時(shí)鐘為研究對象.

問題6若時(shí)間慢了25分鐘，則校對時(shí)間后，分針旋轉(zhuǎn)形成的角為多少？

問題7若時(shí)間快了10分鐘，則校對時(shí)間后，分針旋轉(zhuǎn)形成的角為多少？

問題8若以分針在3點(diǎn)時(shí)刻為起始邊，旋轉(zhuǎn)90°后，角的終邊在什么位置？

問題9在問題8的基礎(chǔ)上，再旋轉(zhuǎn)-30°后，角的終邊在什么位置？

問題10情境中的直角、平角、周角是象限角嗎？

設(shè)計(jì)意圖以學(xué)生的生活經(jīng)驗(yàn)為基礎(chǔ)，提出問題，學(xué)生的熱情一下子被激發(fā)起來，答案也多種多樣.如：時(shí)鐘、車輪、音量旋鈕、排氣扇、剪刀、扳手、體操、跳水等都是旋轉(zhuǎn)形成正、負(fù)角很好的例子.時(shí)間快慢的校準(zhǔn)可以幫助學(xué)生進(jìn)一步強(qiáng)化按逆時(shí)針方向旋轉(zhuǎn)形成的是正角，按順時(shí)針方向旋轉(zhuǎn)形成的是負(fù)角.另一方面，旋轉(zhuǎn)要確定起始邊和終邊.為了研究問題的方便，我們引入平面直角坐標(biāo)系，將角的頂點(diǎn)放在坐標(biāo)原點(diǎn)，起始邊放在x軸正半軸上，從而終邊(除頂點(diǎn)外)在哪個(gè)象限，就稱這個(gè)角為第幾象限角，終邊落在坐標(biāo)軸上的角稱為軸線角.

2.3 巧妙組織課堂活動(dòng)，提升學(xué)生的思維水平

若以時(shí)鐘的分針為研究對象，分針在3點(diǎn)時(shí)刻的位置作為起始邊，你能否轉(zhuǎn)出60°角？在60°角的基礎(chǔ)上，請轉(zhuǎn)出下列角：420°,780°,1 140°,-300°,-600°.完成下列填空題，并回答相應(yīng)問題.

420°=60°+______360°，

780°=60°+______360°，

1 140°=60°+______360°，

-300°=60°+______360°，

-600°=60°+______360°.

問題11根據(jù)上述經(jīng)驗(yàn)，與60°角終邊相同的角β可以表示為______.

問題12與任意角α終邊相同的角β可表示為______.

結(jié)論一般地，與角α終邊相同的角的集合為β|β=α+k·360°,k∈Z.

設(shè)計(jì)意圖通過學(xué)生自己動(dòng)手實(shí)踐，邊動(dòng)手、邊思考、邊歸納，感知420°,780°,1 140°,-300°,-600°角都是與60°角終邊相同的角，它們之間相差360°的整數(shù)倍.通過設(shè)疑來激發(fā)學(xué)生的思維，讓學(xué)生體會(huì)從具體到抽象、從特殊到一般，逐步歸納得出一般性結(jié)論.

2.4 巧妙設(shè)計(jì)數(shù)學(xué)例題，培養(yǎng)學(xué)生的數(shù)學(xué)能力

例1寫出與下列角終邊相同的角的集合，并在0°～360°范圍內(nèi)，找出與之終邊相同的角.

(1)650°;(2)-150°;(3)-990°15′.

問題13你能判斷上述各角是第幾象限角嗎？

問題14290°是第幾象限的角？

設(shè)計(jì)意圖例1在教材的基礎(chǔ)上增加了寫出終邊相同角的集合的過程，目的是幫助學(xué)生快速找到思路，通過問題13強(qiáng)化判斷象限角的方法.問題14的目的是引入“形”，從形的角度理解找終邊相同的角和判斷象限角的方法，即順時(shí)針、逆時(shí)針旋轉(zhuǎn)幾個(gè)整數(shù)圈的問題.

設(shè)計(jì)意圖教材中采用代數(shù)方法處理例2，利用代數(shù)方法求解，需要分奇數(shù)、偶數(shù)討論，學(xué)生不易理解.這里可以借助問題引導(dǎo)學(xué)生從“形”的角度思考，問題如下：終邊相同的角的集合公式中與k相乘的角的度數(shù)是“360°”，而這里是“180°”，他們有什么區(qū)別和聯(lián)系呢？學(xué)生從形的角度，理解了轉(zhuǎn)一圈和半圈后，問題就迎刃而解了.

思考題(1)終邊落在x軸上的角的集合如何表示？

(2)終邊落在坐標(biāo)軸上的角的集合如何表示？

設(shè)計(jì)意圖從正、反2個(gè)方面思考問題，進(jìn)一步加強(qiáng)對圖形本質(zhì)的理解.

3 反思教學(xué)內(nèi)容，提升探究能力

(1)知識(shí)結(jié)構(gòu)：

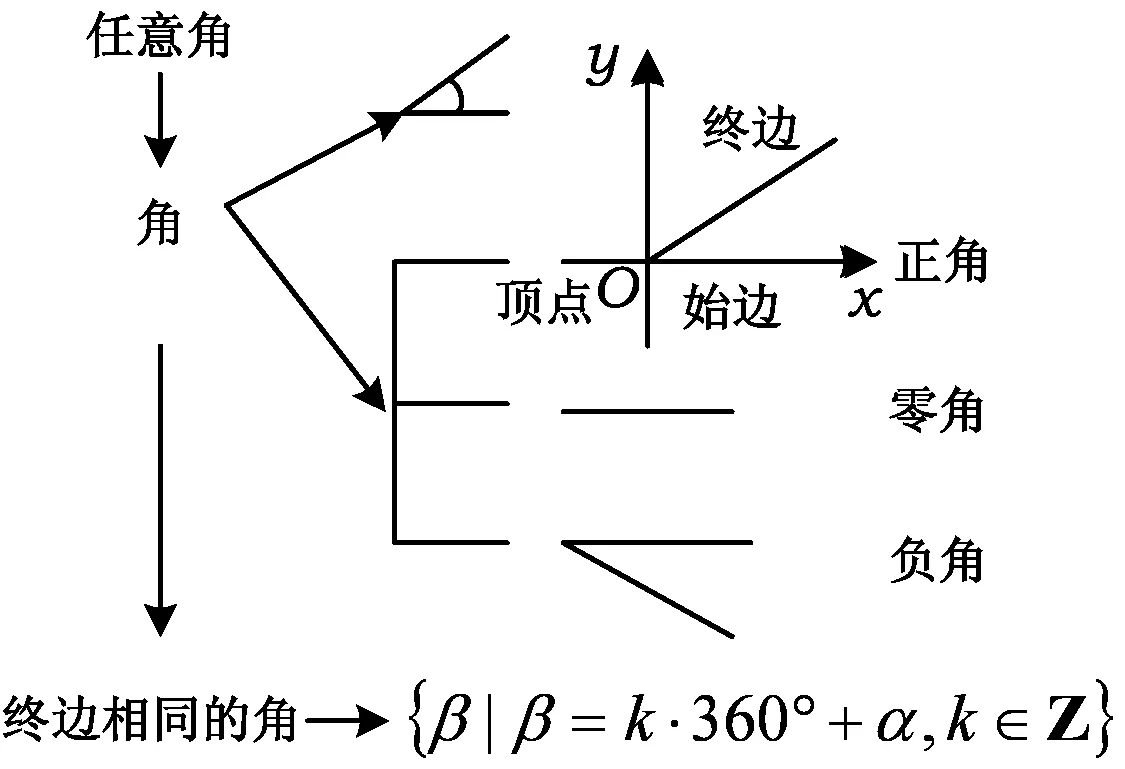
(2)探究方法：類比、歸納、猜想、驗(yàn)證.

(3)拓展探究：請利用互聯(lián)網(wǎng)搜集與角的概念有關(guān)的數(shù)學(xué)故事，并相互交流.