例說(shuō)如何巧“挖”三角問(wèn)題中的隱含條件

●

(鎮(zhèn)海中學(xué) 浙江寧波 315200)

例說(shuō)如何巧“挖”三角問(wèn)題中的隱含條件

●胡勇

(鎮(zhèn)海中學(xué) 浙江寧波 315200)

在解有關(guān)三角的問(wèn)題中，許多學(xué)生出現(xiàn)增解和錯(cuò)解.其原因不是不會(huì)解答這些題目，而是沒(méi)有充分挖掘隱含條件.如何充分挖掘三角問(wèn)題中的隱含條件，從哪里“挖”，怎么“挖”，學(xué)生往往感到困惑和迷茫.對(duì)此，筆者根據(jù)自己多年的教學(xué)實(shí)踐，通過(guò)對(duì)以下幾個(gè)典型例子的剖析，并以此拋磚引玉，談?wù)勅绾吻伞巴凇比菃?wèn)題中的隱含條件.

1 全面深入審題，挖掘題設(shè)隱含條件

例1在△ABC中，內(nèi)角A,B,C所對(duì)的邊分別是a，b,c,且sinC=2sinB，求函數(shù)

的值域.

(2013年寧波市高三“十校”聯(lián)考數(shù)學(xué)試題)

而

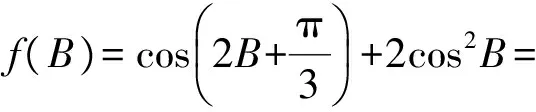
則

于是

從而

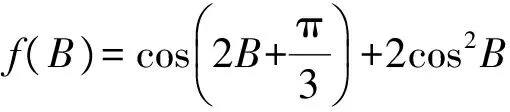
sinC>sinB,

從而

C>B,

得

又因?yàn)?/p>

所以

正解在△ABC中，因?yàn)閟inC=2sinB>0，所以

sinC>sinB.

又因?yàn)?/p>

所以

從而

得

于是

2 掌控解題過(guò)程，挖掘轉(zhuǎn)化隱含條件

例2若3sin2α+2sin2β-2sinα=0，則cos2α+cos2β的取值范圍是

( )

(2013年浙江省鎮(zhèn)海中學(xué)《數(shù)學(xué)(必修5)》模塊評(píng)價(jià)考核試題)

cos2α+cos2β= 2-sin2α-sin2β=

又因?yàn)?/p>

|sinα|≤1，

所以

故選A.

cos2α+cos2β= 2-sin2α-sin2β=

故選D.

3 審視解題結(jié)果，挖掘題目隱含條件

例3已知0<α<β<γ<2π,且sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0，則β-α的值為_(kāi)_______.

(2013浙江省鎮(zhèn)海中學(xué)《數(shù)學(xué)(必修4)》“三角恒等變換”單元練習(xí)題)

錯(cuò)解由條件得

sinα+sinβ=-sinγ，cosα+cosβ=-cosγ，

兩式平方相加，得

2+2cos(α-β)=1，

于是

則

正解由條件得

sinα+sinβ=-sinγ，

cosα+cosβ=-cosγ,

兩式平方相加，得

2+2cos(α-β)=1，

于是

則

這與題設(shè)條件矛盾.于是

以上是筆者總結(jié)的在處理三角問(wèn)題中對(duì)隱含條件挖掘應(yīng)該注意的地方.我們只要在解三角問(wèn)題過(guò)程中引導(dǎo)學(xué)生注意到以上3個(gè)方面，并能夠舉一反三，且在解題的審題、解答過(guò)程和結(jié)果等各個(gè)環(huán)節(jié)都具有挖掘隱含條件的意識(shí)，就能夠大大提高解三角問(wèn)題的準(zhǔn)確性、嚴(yán)密性和嚴(yán)謹(jǐn)性，進(jìn)而發(fā)展智力、鍛煉思維、提高能力.

[1] 胡勇.一個(gè)不容忽視的問(wèn)題——隱含條件的挖掘[J].數(shù)學(xué)通訊,2002(14/16):83.

[2] 波利亞.怎樣解題[M].涂泓,馮承天,譯.上海:上海科技教育出版社,2002:35-38.

[3] 戴再平.數(shù)學(xué)習(xí)題理論[M].上海:上海教育出版社,1991:147-161.