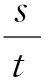堅持標準 關注本質 引領教學
——2012年浙江省臺州市學業水平考試命題的實踐與思考

●

(仙居縣教研室 浙江仙居 317300)

堅持標準關注本質引領教學
——2012年浙江省臺州市學業水平考試命題的實踐與思考

●吳增生

(仙居縣教研室 浙江仙居 317300)

初中畢業生數學學業水平考試是一種標準參照考試，其功能是評價學生初中階段數學學習達成課程標準要求的水平，這類考試還承擔了高中招生選拔的功能.正是這種功能，引起了學校的高度重視，同時出現了“壓縮新課教學進程、長時間復習、大運動量訓練”等不良教學現象，給學生造成了過重的學習負擔.在堅持標準參照考試性質，適當體現學習潛能評價，科學合理評價學生的學業水平的基礎上，充分發揮區域性考試的教學導向功能，雖然對扭轉不良教學現象不能起釜底抽薪的作用，但還是有一定的作用.基于此，2012年臺州市學業水平考試試題，在繼承前幾年特色的基礎上，作出了適當的調整與創新.

1 堅持標準

堅持標準要求命題以課程標準和考試說明為依據，這是保證標準參照考試性質的前提，也是科學合理地評價學生學業水平的基礎.

整卷布局按照容易題、稍難題和較難題的權重(分值)7∶2∶1進行，關注在核心知識的中間地帶命制試題，重點考核心知識和思想方法，穿插考一般知識.

如對函數的考查，第7題考查反比例函數的增減性；第19題考查反比例函數和正比例函數的解析式和圖像；第23題考查二次函數的圖像及性質；第24題又考查了用函數表示幾何度量的變化規律.既覆蓋了初中3類基本函數，又重點考查了函數模型思想；既以函數增減性這一核心知識為考查重點，又兼顧了函數解析式、函數圖像等相關知識.其中第7題為容易題，第19題為稍難題，第23題和第24題為較難題.

再如，幾何的核心知識是三角形、平行四邊形和圓的基本性質、圖形的全等變換(包括平移、軸對稱和旋轉)及相似三角形的性質和判定，對這些核心知識的考查體現在第2～4,6,10,14～15,22,24題中.其中第2～4,6,14題為容易題，第15題和第22題為稍難題；第10題考查菱形的軸對稱性、銳角三角形函數，要求運用圖形變換思想解決問題，屬于較難題；第24題是新的幾何對象及其性質的探究，涉及到的知識點有：平移、平行線、勾股定理、相似三角形、矩形、圓、函數、方程、不等式等，涉及到的數學思想方法有：分類討論思想、數形結合思想、方程思想、數學類比等，是新背景下的數學對象的探究，屬于較難題.

對于統計和概率領域的考查，以統計分析和決策為考查重點.如第8題考查統計量意義的理解，而不考查統計量的計算；第21題考查在現實背景下的數據分析和決策過程.

考慮到學習困難學生的實際情況，容易題比往年更簡單.如第1～7,11～13題都只考查一個知識點，共計43分.第17題和第18題都是簡單的代數計算和解一元一次不等式組問題，共計16分.這樣，最簡單的題就有近60分，而且在綜合題中，也有容易得分的小題，整卷的基礎性體現得比較充分.

2 關注本質

關注本質，就是要關注數學最顯著的學科特點——抽象性、邏輯嚴謹性和應用廣泛性；重視數學抽象概括、模型和推理計算這3個基本思想；重視數學應用；關注初中數學常用的數學思想方法如分類討論、數形結合、函數方程、數學模型、圖形變化、數學轉化、特殊化與一般化的考查；重視諸如數學感知、數學表征、數學抽象概括、數學推理計算等認知水平的考查；重視知識的理解、思想方法的感悟；重視數學大智慧，而不是追求解題小技巧.

如第24題創設了數學概念學習和幾何探究的新背景，以距離這一幾何核心概念為出發點，引進了兩線段之間距離這一新概念，這一概念與兩點之間的距離、點到直線之間的距離、2條平行直線之間的距離等概念相聯系，要求學生理解這一新概念并用這一概念表示和研究圖形的性質.在這個問題的解決中，包含了對概念理解、解釋、運用的考查.在理解這一概念過程中，需要比較初中階段學習過的幾種距離概念，理解平移的概念，需要用新概念描述線段的平移，想象“兩線段之間距離為2”的幾何模型,需要用函數觀點、數形結合、方程的思想分析和解決問題.總之，該題對數學感知、數學表征、數學抽象概括、數學推理計算等數學認知水平進行了全面的考查.第24題原題如下：

定義：P，Q分別是2條線段a和b上任意一點，線段PQ長度的最小值叫做線段a與線段b的距離．已知O(0，0)，A(4，0)，B(m，n)，C(m+4，n)是平面直角坐標系中4個點．

(1)根據上述定義，當m=2，n=2時(如圖1)，線段BC與線段OA的距離是______；當m=5，n=2時(如圖2)，線段BC與線段OA的距離(即線段AB長)為______．

(2)如圖3，若點B落在圓心為A，半徑為2的圓上，線段BC與線段OA的距離記為d，求d關于m的函數解析式．

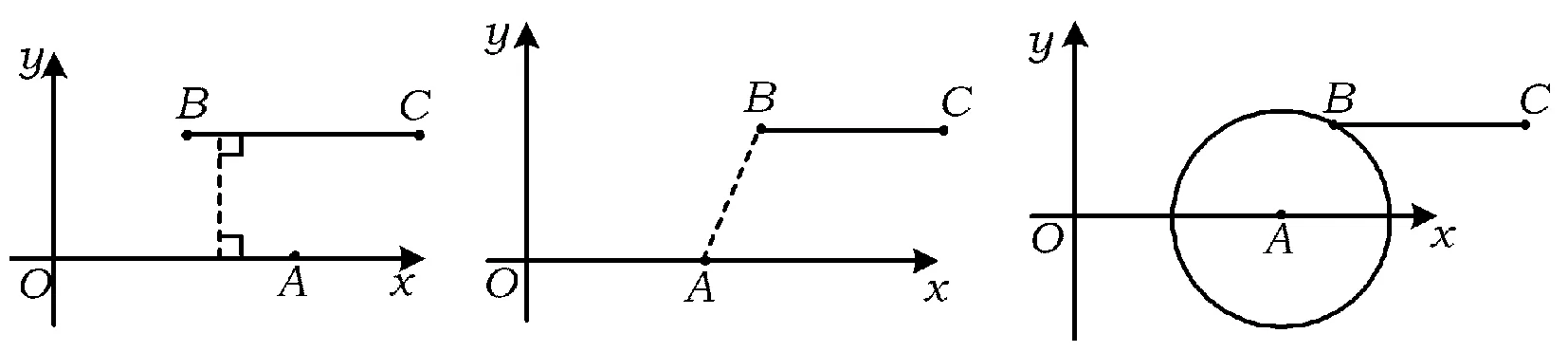
圖1 圖2 圖3

(3)當m的值變化時，動線段BC與線段OA的距離始終為2，線段BC的中點為M．

①求出點M隨線段BC運動所圍成的封閉圖形的周長.

②點D的坐標為(0，2)，m≥0，n≥0．作MH⊥x軸，垂足為H.問是否存在m,使以A，M，H為頂點的三角形與△AOD相似?若存在，求出m的值;若不存在，請說明理由(備用圖如圖4和圖5所示)．

圖4 圖5

再如，第16題：

請你規定一種適合任意非零實數a，b的新運算“a⊕b”，使得下列算式成立：

1⊕2=2⊕1=3；

…

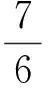
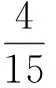
你規定的新運算a⊕b=________(用含a，b的一個代數式表示).

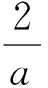
第23題改編于人教版教材中的習題：

某汽車在剎車后行駛的距離s(單位：米)與時間t(單位：秒)之間關系的部分數據如表1所示：

表1 剎車后行駛的距離與時間之間的關系

假設這種變化規律一直延續到汽車停止．

(1)根據這些數據在圖6的坐標系中畫出相應的點.

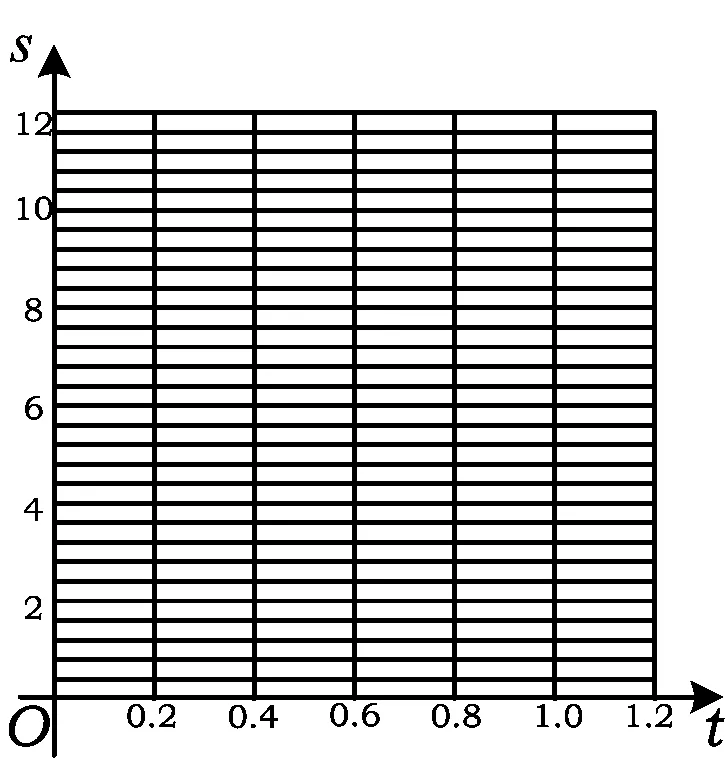
圖6

(2)選擇適當的函數表示s與t之間的關系，求出相應的函數解析式.

(3)①剎車后汽車行駛了多長距離才停止？

在近幾年的考試中，有2類函數題型出現的頻率非常高：一類是以圖像為背景的有解析幾何傾向的問題；另一類是用函數研究圖形變化下的某些度量屬性的變化規律.其實，函數最明顯的特征是模型屬性而非圖形屬性，畫函數圖像是為研究函數的性質服務的，而不是為了研究圖像而研究圖像.雖然初中的函數具有數形結合的特點，與高中解析幾何有著密切的聯系，但作為學業水平考試，應該重點關注其本質特征.第23題就是回歸函數的本質屬性，關注函數的模型屬性，考查了學生根據部分對應關系合理選擇函數類型進行模擬并求出函數解析式，研究函數的最值，體現了函數思想中“考查回歸本質、重視知識應用”的命題思想.

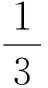
3 引領教學

作為與學生升學有關的大型區域性考試，導向教學是學業水平考試的重要功能.在當前教學實踐中，普遍存在著重教輕學、重訓練輕理解、重知識輕思想、重結果輕過程、重技巧輕智慧的現象.這些教學中的不良價值取向的核心原因是應試教育思想在作祟.教師不重視在課堂教學中讓學生通過獨立思考和相互交流理解知識、體會數學思想.概念教學“一個定義、三點注意”，拼命把知識塞給學生，再通過大量練習進行鞏固.新課教學囫圇吞棗趕進度，留出大量的時間搞訓練型復習.在復習教學中，沒有讓學生通過自己的思考理解知識之間的相互聯系，建立知識網絡，而是以過度訓練來達成解題熟練和提高解題速度.不是認真研究課程標準、考試說明和教材，而是熱衷于做大量中考陳題，熱衷于猜題壓題.作為學業水平考試的命題者，擔負著引領教師、摒棄這些教學弊端、改進教學的責任.

怎樣才能使學業考試擔負起這一使命呢？

首先，應該全面貫徹課程標準和考試說明，把握試卷的整體難度，本卷總體難度為0.70左右,符合考試說明的要求.

其次,要重視對數學知識的理解和數學思想方法的感悟,重視大智慧,摒棄小技巧.如第16題著重考查數學概括,而很少涉及具體的知識;第10題著重考查對稱思想;第24題重點考查對數學新概念的理解和應用,考查學生用所學概念進行解題的能力，研究新概念對象的幾何性質.