新穎賽課 實現共贏
——一次優質課賽課的親歷及感悟

●

(顧國和中學 浙江寧波 315800)

新穎賽課實現共贏
——一次優質課賽課的親歷及感悟

●張良江

(顧國和中學 浙江寧波 315800)

2011年11月，寧波市北侖區教研室組織了初中數學優質課評比活動．筆者作為學校教研組一員參與了選手賽前的磨課，并以評委的身份親歷了賽課的全過程，有頗多感悟和收獲，現撰文與同行交流．

1 賽前過程回眸

1．1 內容與形式

一般的賽課，多見于新授課或復習課，而本次賽課的組織者只給選手提供了一道2011年浙江省寧波市的中考試題，要求“課題自行確定，內容自行組織，但教學內容中必須有規定的題目”．原題(以下簡稱“賽題”)如下：

閱讀下面的情景對話，然后解答問題：

題目師：我們新定義一種三角形，2條邊的平方和等于第3條邊平方的2倍的三角形叫做奇異三角形.

小華：等邊三角形一定是奇異三角形！

小明：那直角三角形中是否存在奇異三角形呢？

(1)根據“奇異三角形”的定義，請你判斷小華提出的命題：“等邊三角形一定是奇異三角形”是真命題還是假命題？

(2)在Rt△ABC中，∠ACB=90°，AB=c，AC=b，BC=a，且b>a.若Rt△ABC是奇異三角形，求a∶b∶c.

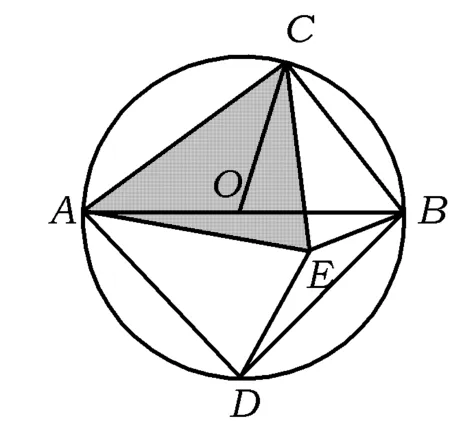
圖1

①求證：△ACE是奇異三角形；

②當△ACE是直角三角形時，求∠AOC的度數．

1．2 研題與磨課

在選手們接受賽課任務之后，筆者與其他教師參與了該賽題的研討、挖掘，著手進行了對該課內容及整節課的設計：先嘗試確定課題、課型和內容，初步定出整節課的流程與環節，落實基本框架．通過若干次的試教，不斷加工磨礪，使該課的內容漸趨充實，結構漸趨緊湊，過渡銜接漸趨自然流暢，以提升能力、提煉數學思想的立意漸趨高遠．

萬事俱備，只待賽課！從賽課的實況可以看出，各選手基本上都是以所給賽題為主干，從對賽題的深度解讀、引申或拓展等角度入手，繼而在發展學生思維、總結解題方法和規律、提煉數學思想等方面進一步展開．

2 案例呈現及評析

筆者作為評委，親歷了5位選手賽課的全過程，他們設定的課題如表1所示．

表1 5位選手設定的課題

從表1中可以看出，除了1位選手將課題定位于“特殊三角形的邊角關系”，其余4位選手對課題的定位基本一致，教學內容和教學重心也大致相同．回觀賽課的各個環節，不乏精彩片斷，現擷取一二并予以評析．

2．1 別樣引入，百花齊放春滿園

在課題引入階段，選手們也各顯其能，作了不同的情境創設，采用了豐富的引入方式．

案例1

師：三角形是多邊形中最基本的一種，許多多邊形問題都可以轉化為三角形問題．同學們，組成三角形的元素有哪些呢？

生：3條邊和3個角．

師：對！同學們看到三角形的3條邊會產生哪些聯想？

生：三角形任意兩邊之和大于第三邊(任意兩邊之差小于第三邊)．

師：你還想到哪些結論？

生：勾股定理．

師：很好！勾股定理是直角三角形特有的性質，即由直角三角形可得“a2+b2=c2(其中c是斜邊)”．反之由“a2+b2=c2(其中c是最長邊)”也可以得到此三角形為直角三角形．那么在三角形中，是否存在兩邊的平方和等于第三邊平方的2倍的三角形呢？如果存在，此類三角形又有哪些特有的性質呢？同學們愿意一起來探索和研究嗎？

生：愿意！

評析課堂伊始，教師通過創設問題情境，點明了本節課的學習方向，激起了學生的主動學習意向．從學生已有的知識經驗出發，貼近學生的最近發展區，激起學生“跳一跳，摘桃子”的探究欲望．新情境的創設，拉近了師生間的距離，打開了學生的思維之門，不露聲色、自然流暢地將學生引入到對未知情境的探究之中．

2．2 深究詳析，撥開云霧見天日

在對“奇異三角形”這一概念的剖析過程中，選手們也有代表性的探究設計．

案例2

表2給出了5組a，b，c的值，以a，b，c為邊構成的三角形是否為“奇異三角形”？請作出判斷，并說明理由．

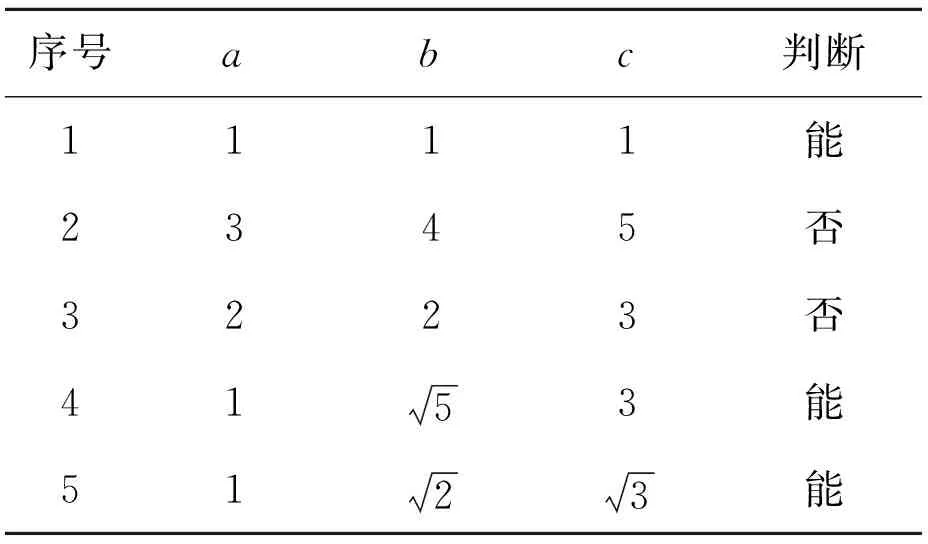
表2 a,b,c的值

師：同學們，觀察表2中的第2組a,b,c的值，邊長分別為“3，4，5”的三角形是怎樣的三角形？它是奇異三角形嗎？

生：是直角三角形；但不是奇異三角形．

師：那能不能說“直角三角形都不是奇異三角形”呢？

師：非常好！這么說直角三角形也有可能是奇異三角形，大家從第3、第4、第5組數值又分別能夠得到怎樣的猜想呢？

生2：非等邊的等腰三角形必定不是奇異三角形.

……

教師在解答完第(2)小題的基礎上又引導學生將前面的各個猜想進行歸納，并逐一驗證．

(1)奇異三角形(非等邊)中“a2+b2=2c2”的c必定為中長邊；

(2)等邊三角形都是奇異三角形；

(3)非等邊的等腰三角形一定不是奇異三角形；

(4)直角三角形中有的是奇異三角形，有的不是；

(6)所有的奇異直角三角形都相似．

評析表格對于呈現數量關系有獨特的功能．從對奇異三角形的概念進行剖析這一環節來看，案例2的設計高屋建瓴，游刃有余．教師借助表格，精心設問，激發思維，將概念的本質屬性進行充分挖掘，使原本單薄的數學概念變得厚重、充實．同時，也使學生對數學問題的研究方法有了更深的體會．

2．3 巧妙類比，此處無聲勝有聲

在對第(3)小題進行分類討論時，選手們大多將“奇異三角形”與“直角三角形”進行類比．

案例3

師：一個直角三角形的2條邊長分別為3，4，那么第3條邊長為多少？

生1：第3條邊長為5，因為勾3股4弦5．

師：原來如此！這么說，第3條邊的長度有幾種結果？

師：很好！這里并沒有明確告訴我們哪一條邊是斜邊，因此要分成3種情況進行討論，只不過斜邊不可能是3而已．同學們繼續探究下面的問題：已知一個三角形的2條邊長是4和6，則當第3條邊長為________時，此三角形是奇異三角形．

(因為不知道哪一條邊是第3條邊，所以應該分成3種情況.)

接著，在分析第(3)小題第②問的過程中，教師通過類比，引導學生自行分類．

師：第(3)小題第①問已經證明了△ACE是奇異三角形，現在又說△ACE是直角三角形，大家看有沒有明確哪個角是直角？

生：沒有．

師：哦，那你認為哪個角可能是直角，有幾種可能？

生1：有3種可能：∠ACE，∠AEC，∠CAE都有可能是直角．

師：不錯！就像剛才“已知直角三角形的兩邊求第三邊“，我們考慮了3種情況，但是有一種情況被排除了，這里是否可以排除哪個角是直角呢？

生2：∠ACE肯定不是直角．

師：為什么？

生2：因為第①問已經證明了△ACE是奇異三角形，并且AC2+CE2=2AE2，這樣可以得到AE是中長邊.如果∠ACE是直角的話，則AE是斜邊，而斜邊必定是最長邊．顯然這是不可能的，因此∠ACE不可能是直角．

師：太棒了！

(眾生鼓掌.)

師：那么就是說只有2種可能了．分別畫出這2種情況的圖形看看……

評析類比是極其重要的數學思想．通過類比，將新知建立在已有知識、經驗的基礎上，將舊情境中的方法自然地遷移到新問題的解決中來，有一種水到渠成的感覺．案例3通過將“奇異三角形”與“直角三角形”進行類比，將復雜的問題簡單化，將分類思想自然地融入在精心的鋪墊中，化解了難點，內化了數學思想方法，提升了分析解決問題的能力．

2．4 自然延伸，愛你在心口難開

當解答完整道題后，教師繼續利用幾何畫板進行動態演示，拖動點C，出現了如圖2所示的情形，此時點E在⊙O的外部；繼續拖動點C，出現圖3和圖4的情形，點E消失，即△ACE不存在了．

圖2 圖3 圖4

案例4

師：同學們可以看到，隨著點C的位置變化，點E可能在⊙O內，也可能在⊙O外.當點E在⊙O內時，我們已經證明了△ACE是奇異三角形，那么當點E在⊙O外時，△ACE還是奇異三角形嗎？

生：是的，證明方法是一樣的．

師：大家再觀察一下圖3和圖4，為什么點E會消失呢？也就是說△ACE為什么會不存在了呢？△ACE存不存在由什么來決定呢？

(學生思考.)

師：我們先來看看點E是如何產生的．

(教師再次進行動態演示.)

師：分別以點C,A為圓心，CB,CA為半徑畫圓，這2個圓的交點就是點E．從B向A拖動點C，會發現隨著點C位置的變化，2個圓會產生不同的位置關系．同學們再考慮，當點E位于⊙O的內部時，2個圓處于怎樣的位置關系？若假設AB=4，此時線段CB的取值范圍是怎樣的？

(教師反復演示動畫.)

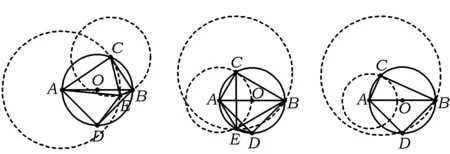
圖5 圖6 圖7

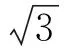
評析“疑是知之始”，質疑能力比解題能力往往更為重要．此案例中，教師的演示和提問，看似無意，實則意味深長．教師正是基于自身對賽題的深入研讀而提出了高品質的問題，為鼓勵學生大膽質疑樹立了典范．案例4就如何“研題”給我們指明了一個方向，這就是：只有教師自身真正觸及數學問題的本質，才能引領學生深入地理解問題；只有教師自己登高望遠，才能使學生在浩瀚的題海中，舉重若輕，才能“會當凌絕頂，一覽眾山小”．

3 賽后啟示及感悟

3．1 賽課形式值得借鑒

本次優質課賽課，只給選手提供一道中考試題，然后要求“課題自行確定，內容自行組織，但教學內容中必須有規定的題目”，這種形式不同于以往以新授課為主的賽課．一般的新授課(或其他的指定課題)，都有大致的框架和流程可供參照，而“只給定一道考題，課題自行確定”的賽課形式則需選手全力以赴，必須最大限度地調動自身的儲存與研讀設計能力．這樣使得選手廣泛聽取同行的意見，為己所用．

3．2 有利于促進教師業務的整體提高

這種形式的賽課活動，整體地推動了區域教師特別是青年教師的快速成長．首先，對于參賽者本人自不必說．其次，對于沒有參賽的年輕教師來說，他們與選手一同設計、評議、修改和優化，在無聲中成長．再次，選手的磨課經歷給各位年輕教師提供了樣板，他們似乎也提前充當了參賽者的角色．另外，稍長者由于要充當引領的角色，自然也不敢怠慢．在這樣的氛圍中，賽者走在幕前既展現了自身的個性特點和綜合素質，又承載幕后團隊協作的強大支撐．最后，沒有參與研題和磨課過程的觀摩教師以及評委親歷了不同選手對同一個問題的不同處理，有比較有鑒別，也往往有茅塞頓開和豁然開朗之感．

總之，通過類似的賽課活動，全體的參與者——選手、團隊成員、觀摩者、評委等等都得到了提升，最終促進了區域教師的共同提高，實現了“共同富裕”，真正做到了以賽促研的效益最大化．近幾年，本區域內有許多年輕教師在經受了這種賽課形式的磨礪之后，迅速成長，他們在市級乃至省級優質課比賽中都取得了佳績．

[1] 施仁智,江建國.在自然的思考過程中催生“新想法”[J].中學教研(數學),2012(3):21-23.

[2] 潘小梅.以賽促研,提升教師專業素養[J].中國數學教育:初中版,2010(11):42-47.