鋪設臺階 引人入勝
——解題教學“一題一課”的實踐與思考

●

(金華市教育局教研室 浙江金華 321000)

鋪設臺階引人入勝
——解題教學“一題一課”的實踐與思考

●傅瑞琦

(金華市教育局教研室 浙江金華 321000)

有效的例題教學，將反饋、鞏固和拓展學生對所學知識的理解與記憶，是學生掌握基本知識、基本技能、基本思想方法和積累活動經驗的重要途徑.通過方法的滲透和體驗，讓學生學會用數學思想方法解決問題，使學生在思維能力、情感態度與價值觀等方面得到協調發展.

但是在教學調研中發現，初三的例題教學，常常就題論題，更多關注學生求解答案的正確與否，關于難點的解決常以一種告訴的方式呈現，不能很好地體會例題中所蘊含的思維方法和思想方法,結論的得出、方法的歸納、思想的提煉沒有充分暴露學生的思維，不能有效地喚醒學生已有的知識,學生就失去了在數學學習過程中發展能力、體現個性的機會.

基于此，筆者所在教研室組織了“一題一課”主題教研活動，本文結合教師2次教學實踐的對比思考，探討如何設計對學生思維有啟發的、能引起學生思考和探索活動的問題來鋪設臺階，有效突破難點，使思維層層深入.

1 例題選用

圖1

(1)若含45°角的直角三角板如圖1所示放置，其中一個頂點與點C重合，直角頂點D在BQ上，另一個頂點E在PQ上．求直線BQ的函數解析式.

(2)若含30°角的直角三角板的一個頂點與點C重合，直角頂點D在直線BQ上，另一個頂點E在PQ上，求點P的坐標．

(2011年浙江省紹興市數學中考試題改編)

2 教學過程

教學設計1

問題引導如圖2，將直角三角板的直角頂點E放在正方形ABCD的頂點A上，三角板的2條直角邊交CD于點F，交CB的延長線于點G，你能得到哪些結論？

生1：∠GAB=∠DAF.

生2：EG=EF，BG=DF…

師(追問)：你能說明理由嗎？

生3：證明△ADF≌△ABG,就可以得出上述結論.

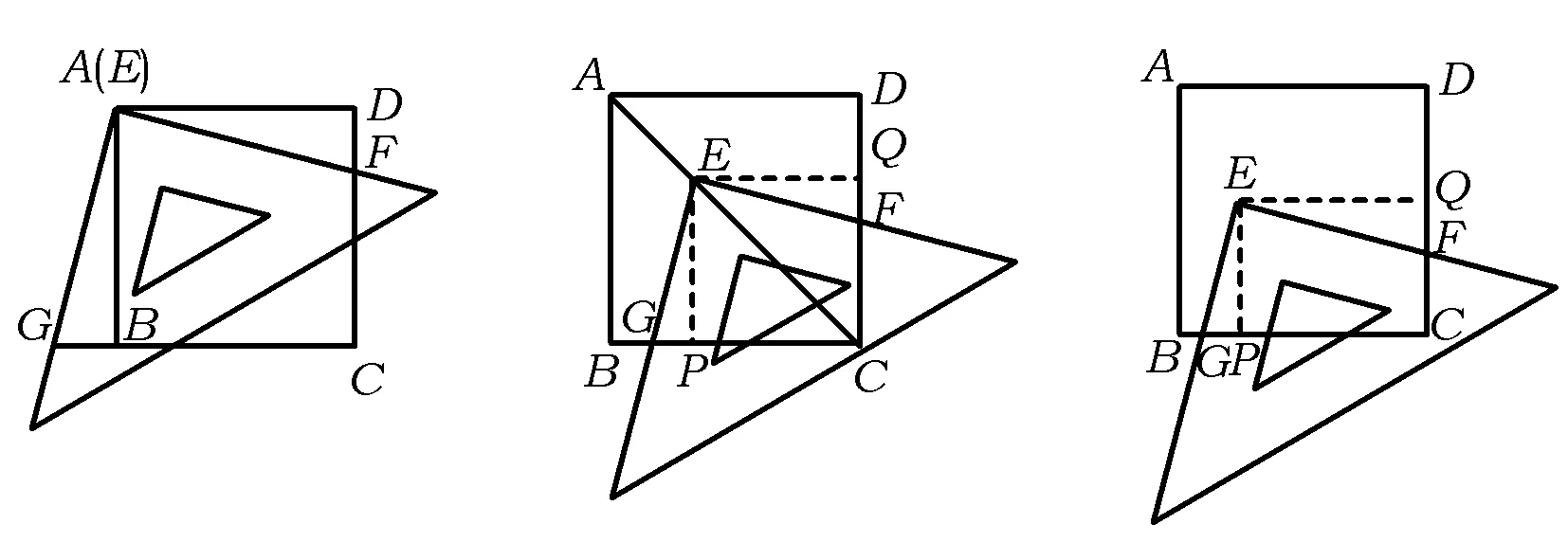
圖2 圖3 圖4

變式1如圖3，如果移動三角板，使頂點E始終在正方形ABCD的對角線AC上，其他條件不變,結論EG=EF是否仍然成立？請你說明理由.

生4：EG=EF仍然成立.

生5：理由是過點E作EP⊥BC,EQ⊥DC，有Rt△EGP≌Rt△EFQ(如圖3)，得EG=EF.

師(小結)：通過圖形對比，聯想構造全等三角形，可得出結論.

變式2如圖4，移動三角板，使頂點E不在正方形ABCD的對角線AC上,結論EG=EF是否仍然成立？

生6：EG與EF不相等.

師：如果過點E作EP⊥BC,EQ⊥DC，你可以得到什么結論？

生7：Rt△EGP與Rt△EFQ相似(如圖4).

師(小結)：弱化條件“點E不在正方形的對角線上”，但圖形的主要特征沒有發生變化，過點E作2條直角邊的垂線，來構造2個相似三角形，得出線段的比例關系.

反思感悟從上面的問題探究中，你能得到什么結論？

圖5

生8：當2個直角對角放置時(如圖5)，通常可以過一直角頂點作另一直角2邊的垂線，構造2個相似(全等)三角形.

師(小結)：構造2個相似(或全等)三角形,實現問題轉化.

解決例題有了圖5基本圖形的提煉，給出例題后學生很快就會想到添加輔助線，順利完成解題:

(1)如圖6，過點D作DM⊥x軸，DN⊥PQ，垂足為M,N，則

△DCM≌△DEN，

于是

DM=DN，

從而

∠DQO=45°，

可求得OQ=4，即Q(4，0)，故直線BQ的解析式為y=-x+4.

圖6 圖7

(2)當點P在對稱軸的右側時(如圖7)，過點D作DM⊥x軸，DN⊥PQ，垂足為M,N.設點(m，0)，則

Rt△CDM∽Rt△EDN，

得

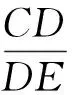
從而

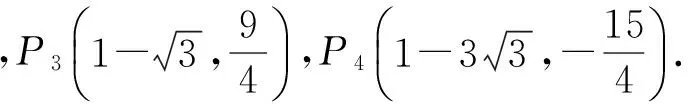
反思這節課，其教學過程是“創設問題情境，構造基本圖形，尋求解題思路”，設計了問題引導及2個變式的臺階，降低思維坡度，學生順利添加輔助線，完成解題.

但是，從課堂觀察看，學生都千篇一律地用圖5作垂線的方法構造全等(相似)三角形來解題，這引發教師的反思，為什么學生解題方法單一，不會尋求另外的解法？基本圖形的構造是學生的難點，“臺階”的設置讓學生順利突破難點，是否太順利了？

于是筆者所在教研室組織了教師研討，對本節課的教學任務、教學目標、示例功能及教學效果等方面進行探討、分析.

教學任務這2個小題的共同之處是圖形特征相同，其區別是三角板擺放位置的不同和內角度數的不同.第(2)小題對30°角分類學生容易想到，但第(1)小題求解時需要添加輔助線，來說明∠BQO=∠CED，對數學感知能力要求較高，是本題的難點.如何突破該難點，教學時需要根據圖形特點，設計問題引導，鋪設思維臺階，引導學生有效思考.

教學目標理解有幾何圖形背景問題的思考方法，利用三角形相似(全等)性質、函數基本性質，以及應用數形結合、函數與方程等數學思想方法來解決問題；培養學生運用動態圖形進行分析、解決問題的能力，增強用分類討論、轉化歸納來分析解決問題的意識；體會提煉基本圖形，感受方程的應用價值，提高根據題意解決問題的縝密思考的習慣.

本課例一開始就以一種告訴的形式呈現2個三角形全等的圖形，問題指向狹窄，學生只是進行機械模仿，易形成思維定勢，束縛了學生的思維，沒有達到教學目標.

示例功能本題是函數背景下常見的動態綜合題型,重點考查學生的數學思想方法及綜合應用能力.2個小題中均隱含著不變的因素，即∠BQO=∠CED，如何說明這2個角相等是解決該題的關鍵.通過本題，引導學生學會獨立思考，根據圖形特征、符號特征等信息，來聯系相關數學知識，添加輔助線，充分經歷數學活動過程，訓練學生的幾何直覺，在探究中培育思維品質，積累解題經驗.

教學效果通過該例的思考解決，能真正體現例題的思維價值，使學生能舉一反三、觸類旁通.

基于這些思考，上課教師著手修改，以教學設計2來組織教學.

教學設計2

(1)創設問題情境，引導探究.

在直角坐標系中，將直角三角板OPE如圖8所示放置，45°角的頂點在原點，過點E作EQ⊥x軸，Q為垂足，聯結QP交y軸于點D,你能夠得出什么結論？并能說明理由.

學生思考5分鐘后,教師要求進行小組交流，并呈現問題串:

問題1如果你還沒有得出滿意的結論，是否可以把三角板放到特殊位置再思考？

問題2你可以畫出哪些特殊位置，結論是什么？

問題3你猜測的結論，在一般情況下是否還成立？試旋轉三角板，判斷你的結論.

問題4如果成立，你能夠說明理由嗎？

圖8 圖9

各小組經探究歸納得出結論:如OD=OQ;△ODQ是等腰直角三角形；DQ平分∠OQE；DQ與x軸的夾角為45°;△DOQ與△OPE相似；……

在思維受阻時，鋪設臺階，引導學生將圖形特殊化，如將三角形的一邊固定在y軸上(如圖9)，或者將邊OE固定在x軸上，得出結論后，再旋轉三角板進行操作驗證，這實際上給出了引導學生探究問題的一種方法——特殊與一般的轉化.

教師繼續呈現如下問題串，隨后組織小組匯報研究成果,教學片斷如下:

問題6從得出的結論看，其本質是“DQ與x軸的夾角45°”，根據圖形特征你可以聯想到什么數學知識？

生1：由“DP是∠OQE的角平分線”聯想到角平分線定理.

師：既然聯想到角平分線定理，能否把圖畫出來，說說你的發現？

學生動手畫圖，1分鐘后回答問題.

生2：過點P作∠OQE兩邊的垂線(如圖10)，這樣就構造了△PMO≌△PNE，從而PM=PN,可得∠PQO=45°.

師：剛才構造全等三角形時充分利用了等腰△OPE的性質，還有其他構造方法嗎？

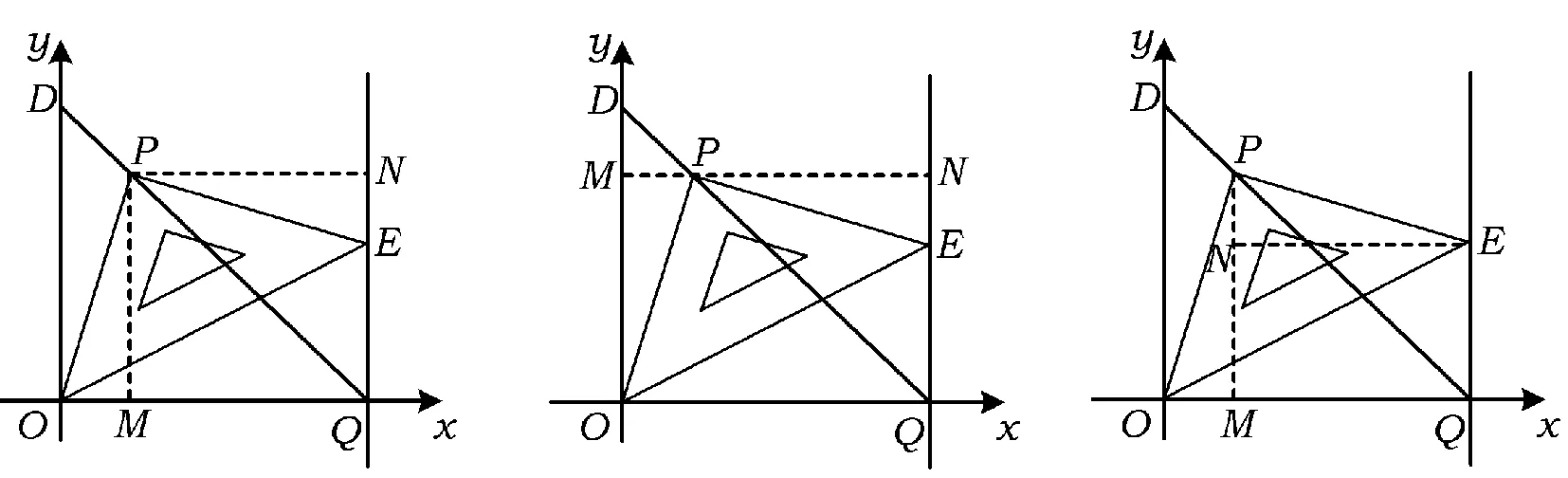
圖10 圖11 圖12

生3：過點P作x軸的平行線，構造△PMO≌△PNE,得PN=QN,從而∠PQO=45°(如圖11).

生4：也可以過點P作PM⊥x軸，過點E作EN⊥PM，構造△PMO≌△PNE來說明PM=MQ,有∠PQO=45°(如圖12).

生5:過點O作OM⊥DQ，過點E作EN⊥DQ(如圖13)，可以構造△OPM≌△PNE,只要說明OM=QM或者EN=QN就可以得到∠PQO=45°.

師：剛才這2種構造的方法，可以看成是由“∠PQE=45°或∠PQO=45°”聯想此角為等腰直角三角形一內角,如圖12，作PM⊥x軸，即可構造等腰Rt△PMQ，我們還可以如何構造等腰直角三角形？

生6：過點P作PM⊥DQ(如圖14)，可以構造△MOP≌△PEQ.

生7：由∠1+∠3=∠2+∠3=90°，得∠1=∠2，又∠MOP+∠POQ=∠PEQ+∠POQ=180°,則∠MOP=∠PEQ，而OP=PE,因此△MOP≌△PEQ,從而PM=PQ,即△PMQ為等腰直角三角形，得∠PQM=∠PMQ=45°.

圖13 圖14 圖15

生8:我發現過點P作PN⊥DQ(如圖15),也可以構造△NPQ≌△OPQ.

師：很好，剛才都是從其中一個45°角來尋求解題思路，另外從圖形特點角度考慮還能聯系什么知識？

生9：由“四邊形OPEQ有2個直角”可以聯想到補全直角三角形.

師：好，大家試試，并說說你的發現.

學生思考，動手在圖上畫，尋求思路.

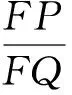
圖16 圖17 圖18

生11：延長OP交x軸于點F,也可以補全Rt△OPF(如圖17)，同樣可求解.

師：剛才有同學注意到“四邊形OPEQ有2個直角”，這個圖形還可以看成什么，可以聯想到什么數學知識？

生12：2個直角三角形Rt△OPE與Rt△OQE有共同斜邊OE.

生13：以OE為直徑作圓.由∠OPE=∠OQE=90°,可知點P,Q都在該圓上，這樣有圓周角∠PEO=∠OQP,從而得結論∠PQO=45°(如圖18).

在這一教學過程中，教師通過問題引導，鋪設思維臺階，從圖形特征、符號信息中聯想其他知識，為添加輔助線提供思考角度，不僅讓學生自己解決了問題，降低了例題難度，更重要的是加強了知識間的聯系，增強了學生探究問題的興趣和思維的發散.

(2)反思解題思路，暴露思維.

在讓各充分小組說出解題思路后，教師引導學生反思解題時的思考，在反思中小結.前6種方法(圖10～圖15)都是由一個45°角聯系到等腰直角三角形的一個內角構造全等三角形，但構造時思考的角度是不一樣的，添加輔助線，實現了轉化；圖16、圖17的方法是基于四邊形OPEQ有2個直角的圖形特點，延長線段補全直角三角形，轉化為三角形相似問題;圖18的方法是基于2個直角三角形有公共斜邊，與圓的知識相聯系，補全圓后，就轉化為圓周角問題；圖10、圖14與圖15的方法，也可以從圖形的旋轉角度去總結.

在解題時，學生往往只關注自己解題時的探究，不理會他人的思考，通過對所有解題分析的反思，分享同伴的解題思路，繼續暴露數學解題的思維.這不是簡單的一題多解，而是從數學思想方法上進行歸納、提煉，使數學解題與智力發展同行.

(3)構造基本圖形，學以致用.

完成例題，要求選用上課沒想到的方法.

(4)適當變式練習，拓展提高.

作業若直角邊之比為2∶3的直角三角形的一個頂點與點C重合，直角頂點D在直線BQ(點D不與點Q重合)上，另一個頂點E在PQ上，試求點P的坐標．

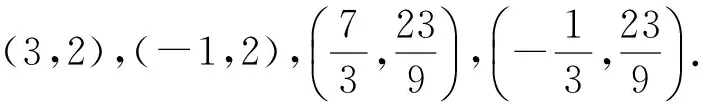
3 教學思考

3.1 鋪設臺階，有效突破學習難點

學習難點的突破，需要創設優化的學習環境，用“問題情境”幫助學生進行數學“意義建構”，2種設計都是在分析例題背景后提煉出幾何模型，幫助學生理解例題所反映的本質.由于三角板是學生熟悉的，起到了“腳手架”的作用，使學生的探究活動得以有效展開，解題時順利添加輔助線，突破難點.

但是，同樣的內容教學，不同的問題創設，達到的教學效果不同.教學設計1解題看似順暢，其實是定性思維，表現為解題思路單一，影響學生思維的展開.教學設計2先讓學生嘗試解決，思考5分鐘無明顯思路,開始呈現問題串，問題串的引領將多個知識點包含在一起，讓學生變換觀察圖形的視角，把自己的注意力集中在問題的引導上，根據圖形特點從不同角度、不同知識產生聯想，使學生的思維可視化，促使學生多角度參與，來提升思考深度,產生不同的解題思路，達到“一題多解”的效果.教師在學生的困難處、受挫時進行引導，受挫后的成功體驗更能激發學生繼續探究的的欲望,激發學習動機.

3.2 問題驅動，加強知識之間聯系

解題教學的目的是以典型例題為載體，通過例題的解答，為學生搭建知識框架，建立知識之間的聯系，使知識系統化，促進學生的認知發展.如何在知識之間建立起合理的、實質的聯系？這就需要問題驅動.2種設計都關注了創設問題情境，來幫助學生對知識的遷移，教學設計1通過問題及其2個變式的引導，從一個基本圖形聯系相似或全等知識.教學設計2圍繞著問題串的思考，從45°角聯想到等腰直角三角形，從一個四邊形2個內角為直角聯想到直角三角形和圓，從等腰直角三角形聯想到圖形的旋轉，并靈活應用相關知識，添加輔助線.設置這類蘊含研究思考過程的問題，學生從中學會聯系、學會轉化，達到鋪設思維臺階的目的.

3.3 關注過程，內化數學思想方法

掌握數學方法和數學思想，形成解題策略及思維品質，是數學教學的目標.這就要求例題教學不能就題論題，而是要把分析探究過程作為一種方法來引導.在依據幾何圖形來解決問題的同時，要設計合理的問題，引導觀察，鼓勵直覺判斷，讓學生參與分析題意、尋求解題思路的過程，體現過程意識.如在教學設計2中，引導學生通過三角板位置的特殊化，來探究結論，根據圖5的圖形特點，以問題串的形式，從不同角度產生對數學知識的聯想，逐步引導學生思考，有效提煉基本圖形，為尋求解題思路提供了可能，歸納出解題的一般方法與特殊方法，讓學生在不同的情境下有多種機會去應用他們所學的知識(將知識“外化”)，經歷數學活動過程，使思維層次不斷提高，從中體會、感悟所蘊涵的思想方法,積累解題經驗.

[1] 羅增儒.怎么樣學會解題[J].中學數學教學參考:初中版，2009(3):7-9.

[2] 顧繼玲.讓學生經歷“數學化”的過程[J].中學數學教學參考:初中版，2011(7):2-4.

[3] 羅增儒.分析解題過程的操作[J].中學數學教學參考:初中版，2009(5):9-14.

[4] 烏美娜.教學設計[M].北京：高等教育出版社,1994.