講清數學道理 揭示數學本質
——提高高三數學復習效率的教學策略

●

(蕭山中學 浙江蕭山 311201)

講清數學道理揭示數學本質
——提高高三數學復習效率的教學策略

●李金興

(蕭山中學 浙江蕭山 311201)

高三學生學得辛苦，但由于缺乏對數學問題本質的認識，常常事倍功半，在重復與茫然的訓練中效率不高．因此，教師的指導作用應該體現在“講清數學道理,揭示數學本質”上.通過教師自身或集體研究，幫助學生反思學習過程、領悟數學背景，從數學知識的根源開始，沿著習題變式的途徑理清每一類問題的來龍去脈，使得數學知識“拎起來成一串、撒下去鋪一片”，這樣才能讓學生舉一反三，實現教學輕負高質的目的.

本文就高三復習階段如何講道理、揭本質例舉幾個典型問題，以期拋磚引玉.

1 新授課講不清的道理，到復習課來講

用斜二測畫法畫幾何體的直觀圖，操作步驟十分簡單：畫軸后，使平行于x軸或z軸的線段長不變，平行于y軸的線段長減半．但按上述方法畫的直觀圖是幾何體的“平行投影”嗎？如果是，投影面和投影線方向如何確定呢？如何描述投影線方向？

文獻[1]對此作了闡述，得到結果：此時投影線與投影面成arctan2角．但這一結果并不能完全確定投影線的方向,可進一步作如下探究：

將水平放置的長方體ABCD-A′B′C′D′的直觀圖(如圖1)看作一個平面圖形(投影)，考慮到平面四邊形ABB′A′、平面四邊形DCC′D′與原圖形全等，因此投影面與長方體側面ABB′A′平行.特別地，不妨以長方體側面DCC′D′所在平面為投影面．

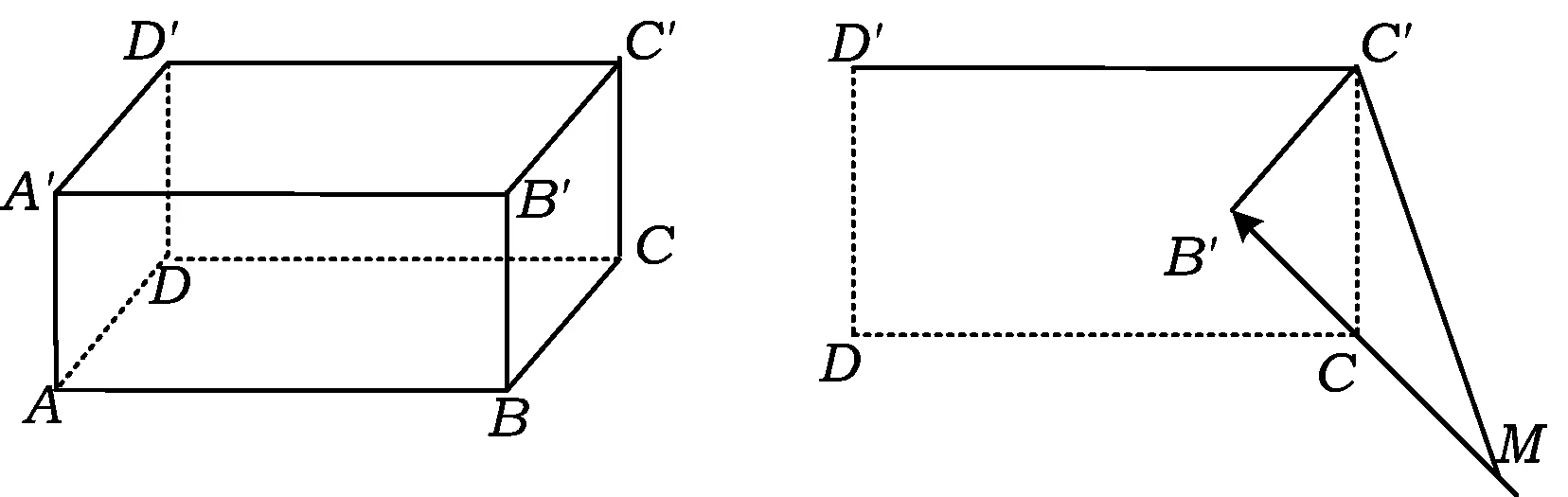
圖1 圖2

圖3

設M(2,0,0)，則

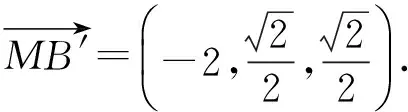
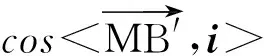
從而投影線與投影面成arctan2角(文獻[1]的結論)．同理，設j=(0,1,0),k=(0,0,1)，可求得

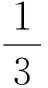
反思斜二測畫法新授課學習時還沒有引入空間向量，因此可以在高三復習課階段補充該知識.

2 學生一錯再錯的道理，將錯就錯地講

2.1 從反例來辨別

先仿照此類錯誤解法，舉例“對于函數y=x2+1(x>0)，因為當x>0時，x2+1≥2x，當且僅當x=1時等號成立，所以當x=1時，ymin=2”，這個結論顯然是錯誤的(明確指出這種解法是錯誤的).

2.2 分析反例錯因

讓學生在同一坐標系中比較y=x2+1和y=2x的圖像，便知“x2+1≥2x”只說明y=x2+1的圖像始終在y=2x圖像的上方，“當且僅當x=1時等號成立”只說明2個圖像相切于點x=1處，切點并非圖像的最低點(如圖4)，y=2也并非函數y=x2+1(x>0)的最小值.

圖4 圖5

2.3 反思錯解成因

3 解題方法巧妙的道理，辯證透徹地講

數學題經常能一題多解，除了常規解法，教師應對“巧思妙解”作辯證分析：有些巧解很難想到，實用性不強；有些巧解變換情景后可能成為錯解，應謹慎采用.

3.1 這樣的巧解對不對

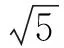
(2008年浙江省數學高考試題)

巧解(錯解) 兩邊求導，得

-sinα+2cosα=0，

從而

tanα=2.

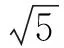
3.2 為何有這樣的“巧思妙解”

例2已知函數f(x)=lnx+ax2+bx(a≤0).

(1)若2a+b+1=0，討論函數的單調性；

參考答案簡述如下：

(2)證明取a=-1,b=1，則

f(x)=lnx-x2+x.

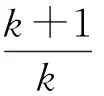
當k取遍1,2,3,…,n并相加，即得

分析對于第(2)小題的答案，學生普遍感到取a=-1,b=1來構造函數f(x)=lnx-x2+x，非常巧妙但很難想到.事實上，若嘗試用數學歸納法證明第(2)小題，則由假設n=k時結論成立推證n=k+1時結論也成立的過程中，只要證明不等式

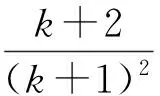
即

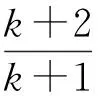
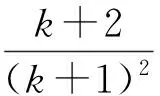
因此只要證當x>1時，lnx

反思對于一些難度較大的問題，若答案過于“巧妙”，則學生容易對這類問題產生“敬畏”之心，不利于數學學習興趣的培養.教師應該讓“巧解”自然呈現其真面目，讓學生有信心去創造“巧妙”解法.

4 學生會而不全的道理，放大細致地講

“細節決定成敗”很多時候能解釋學生“會而不全”的道理，教師講授時要將這些細節放大后細致地講.

圖6

(1)求橢圓C的方程；

(2)求△ABP面積取最大值時直線l的方程.

(2012年浙江省數學高考理科試題)

(2)設AB的中點為M(2t,t)，由點差法易得直線AB方程為

代入橢圓方程,整理得

3x2-12tx+16t2-3=0,

設f(t)=(3-4t2)(1-t)2，則

f(t)=-4t4+8t3-t2-6t+3，

從而

f′(t)=-16t3+24t2-2t-6.

至此，不少學生因為不能對f′(t)的表達式進一步因式分解，導致解題不全.事實上，由f(t)=(3-4t2)(1-t2)得

f′(t)= -8t(1-t)2-2(3-4t2)(1-t)=

-2(t-1)(8t2-4t-3),

反思將f(t)=(3-4t2)(1-t)2的表達式先展開再求導這一細節是導致解題失敗的關鍵因素，教師也可在復習導數應用時專門對此進行針對性復習.

又如2011年全國高中數學聯賽(一試)第7題：

例4直線x-2y-1=0與拋物線y2=4x交于點A,B，點C為拋物線上的一點，∠ACB=90°，則點C的坐標為______.

分析聯立方程，消去x得

y2-8y-4=0，

因此以AB為直徑的圓，其圓心為(9,4)，半徑為

聯立

即可求得點C坐標.該方程組消去x，整理得

y4-56y2-128y-48=0.

至此，不少學生因為不會解四次方程而無法完成解題.事實上，因為點A,B的坐標也是方程組的解，所以上述四次方程必有因式y2-8y-4,從而由

y4-56y2-128y-48=

(y2-8y-4)(y2+8y+12)=0,

解得點C的坐標為(1,-2)或(9,-6).

反思不能利用“A,B的坐標都是方程組的解”這一細節是導致解題失敗的關鍵因素，類似問題在高考題中也有出現，教師應將這種細節放大，培養學生閱讀題意、挖掘隱含條件的意識.

5 類比探究的道理，深入本質地講

從而

即點M與短軸頂點B1,B2的連線的斜率之積為定值.設MB1,MB2與長軸分別交于點P,Q，則

因此

xP·xQ=a2，

而這恰恰就是|OP|·|OQ|=a2的數學本質.

即

從而同樣有定值|OP|·|OQ|=b2.

利用坐標和線段長的對應關系這一數學本質，同樣可研究拋物線相關問題.例如，拋物線y2=2px(p>0)，點A,B,C在拋物線上，BC⊥x軸，AC,AB與x軸交于點D,E，則xD+xE=0，即|OD|=|OE|.

反思典型例題之所以典型在于它反映了數學知識間的一種本質聯系，使解題者能通過一道習題的研究掌握一類問題的解法，使教師能以此為例清晰地剖析出數學知識間的本質聯系，不僅在內容上還能在方法上有利于進一步探究新知.

高中數學和數學教學的道理遠不止本文例舉的幾類.通過教學，教師向學生展示各種數學概念、公式、法則、性質、結論，其目的是讓學生對數學“知其然”；引導學生對數學結論進行推理論證、應用推廣是讓學生對數學“知其所以然”；而向學生講清數學道理、揭示數學本質是讓學生對數學“知其所以所以然”.

“數學要講推理，更要講道理”，如果在教學中只講推理不講道理，那么教師教給學生的僅僅是數學解題的方法和技術，缺乏數學思想的滲透，從而難以提高教學質量.

[1] 沈建剛．斜二測畫法的一次“尋根”之旅[J]．中學數學教學參考,2010(1/2):26．