挖掘數學思想 探究數學本質
——2012年浙江省數學高考函數問題評析

●

(昌碩高級中學 浙江安吉 313300)

挖掘數學思想探究數學本質
——2012年浙江省數學高考函數問題評析

●黃超

(昌碩高級中學 浙江安吉 313300)

函數問題，歷來是高考的重點和難點，也往往是試卷的亮點：初看平淡無奇，細看則韻味悠長；乍看舉步維艱，細想則豁然開朗．浙江卷中的函數試題具有其鮮明的特色，許多問題成為教師津津樂道的經典和師生共同探究的范例，值得細細體會.以下通過對2012年理科第17題的詳細評注和近年來的經典函數試題的簡要分析，與大家一起體驗浙江卷函數問題的特色以及高考復習的方向．

例1設a∈R，若x>0時均有

[(a-1)x-1](x2-ax-1)≥0，

則a=______.

(2012年浙江省數學高考理科試題)

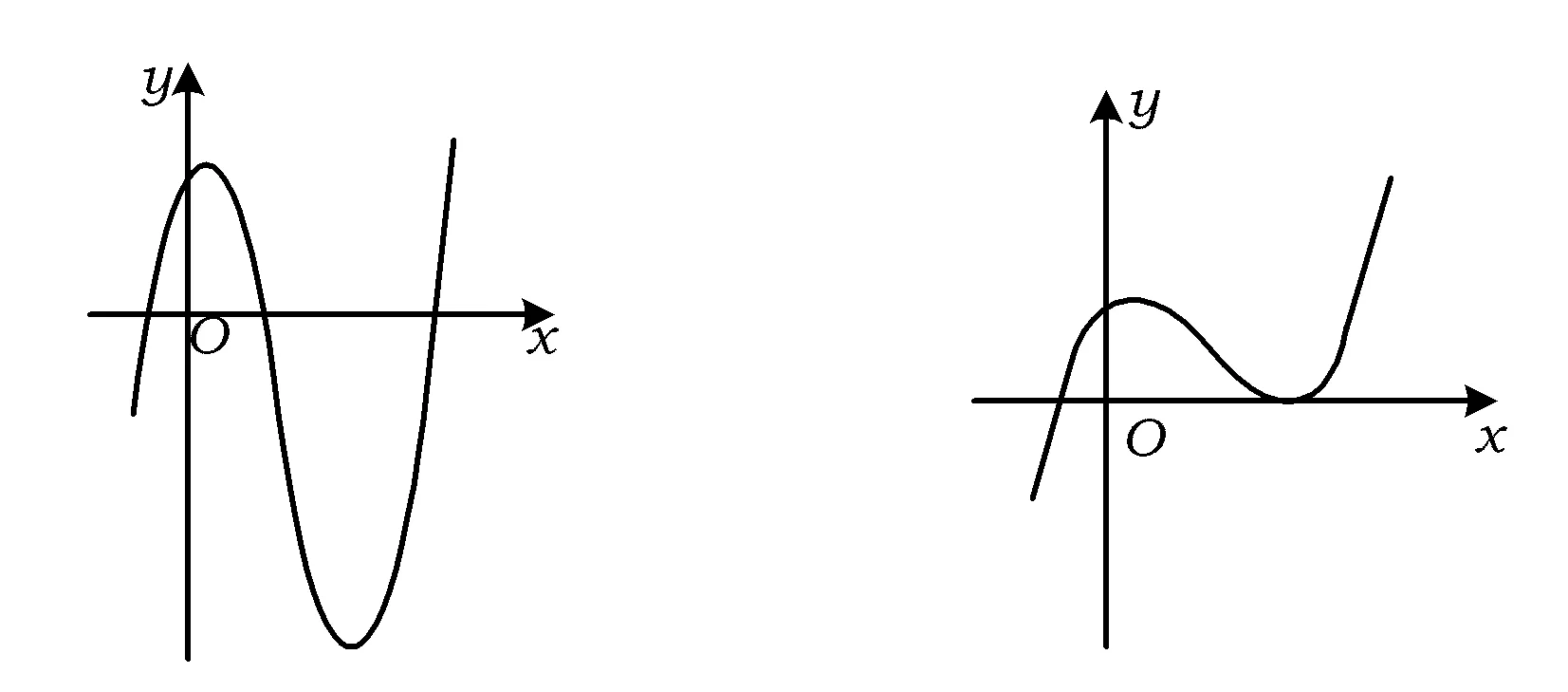
圖1 圖2

注問題的呈現形式為已分解為一次和二次因式乘積的三次多項式不等式求解集，故可以自然聯想到利用三次多項式函數的圖像解題，這是函數思想的直接體現.其以三次多項式函數圖像的整體認知為基礎，經過定性和定量的合理轉化，借助圖像的直觀性可以較順利地發現“等根”這個解題核心，對函數零點的理解是畫圖的關鍵.可能造成解題歧路的是部分學生的思維定勢，即三次多項式函數問題用求導轉化為最值問題來解決，但參數討論的復雜性導致此法行不通.命題者沒有將問題表述為

(a-1)x3-(a2-a+1)x2+x+1≥0，

既在一定程度上指出了問題的思考方向，也在難度上做了較好的控制.這與浙江卷“多考一點想、少考一點算”、“多考通法、少考特殊技巧”等命題理念是緊密相關的，也正是浙江卷的一個鮮明特點.

解法2令f(x)=(a-1)x-1，g(x)=x2-ax-1，f(0)=g(0)=-1,故y=g(x)有正零點.由題意，f(x),g(x)有相同的正零點，如圖3所示，則

因此

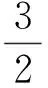
注既然問題已分解為一次和二次因式的乘積，則根據2個函數值正負變化的同步性，將不等式問題轉化為一次函數和二次函數的零點問題，化一般為特殊，以函數圖像作為破解問題難點的切入口，函數、方程、不等式相互轉化，清晰簡潔完滿，體現了數形結合的思想.解題的核心在于以形助數，借助2個函數值的正負變化化簡問題，分合之間彰顯圖像的解題魅力.

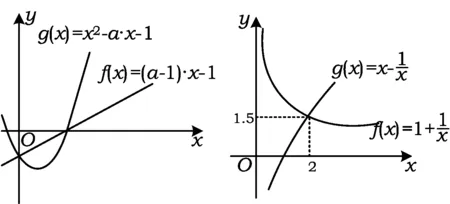
圖3 圖4

解法3由x>0，原不等式可化為

若存在x0>0使得

則

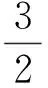
解法4由x>0，原不等式可化為

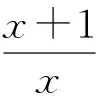
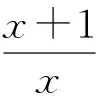
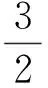
解法5由x>0，原不等式可化為

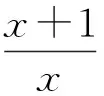
注經過參變分離，將問題轉化為求解關于a的不等式的解集問題，在解法中運用了不等式的“兩邊夾”原理.解法3借助特殊化的思想將問題簡化為方程根的問題；解法4將之轉化為恒成立問題并借助求函數值域的方法；解法5利用函數圖像較為簡潔地說明了問題.從某種意義上說，解法4和解法5也可看作是對解法3的一種解釋.這種包含參變分離的轉化思想也正是解決函數問題的重要方法之一，巧妙的方法背后往往有較為深刻的背景.

解法6當x=2時,

(2a-3)(3-2a)=-(2a-3)2≥0，

因此

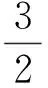
注集簡、巧、靈于一身，如有神助，堪稱絕妙.為什么是x=2？從以上的解法中可以看出這不是巧合，但作為解題，這里顯然有極大的運氣成分.如果解題有障礙，作為應試策略，嘗試代入一些特殊的值不失為一種好的解題方法，這也符合特殊和一般的辨證關系.當然，這樣的妙解多用于欣賞，有時甚至有“事后諸葛亮”之嫌，故不宜大加渲染，度的把握值得注意.

從以上對試題的解答和注看，此題較為清晰地展現了浙江卷中函數問題的鮮明特色，即思想的深刻性、思維的簡潔性、方法的多樣性、圖像的直觀性、函數的二次性，其著眼點在于對數學思想的深刻考查和對數學能力的理性訴求.

1 想一想，思想深刻思路簡

數學思想方法是數學的本質之所在，是數學的精髓.數學思想和方法是數學知識在更高層次上的抽象和概括，它蘊涵在數學知識發生、發展和應用的過程中.高考試題堅持能力立意，對數學思想方法的考查往往是深刻而內蘊的，但在深刻理解的基礎上解題，思路卻是簡潔的.

例2已知a是給定的實常數，設函數f(x)=(x-a)2(x+b)ex，b∈R，x=a是f(x)的一個極大值點,求b的取值范圍．

(2010年浙江省數學高考理科試題)

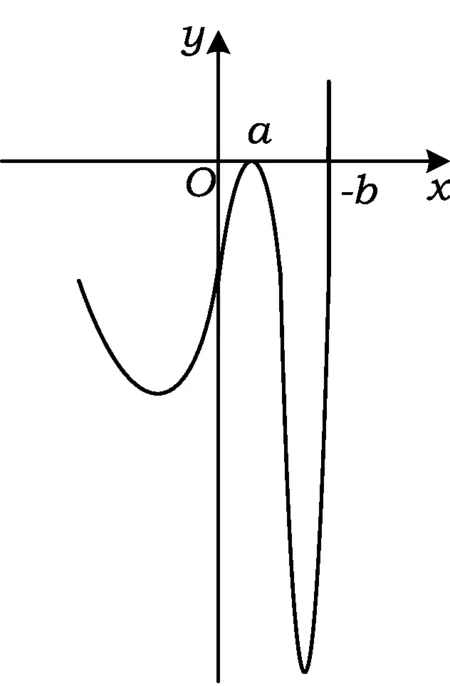
圖5

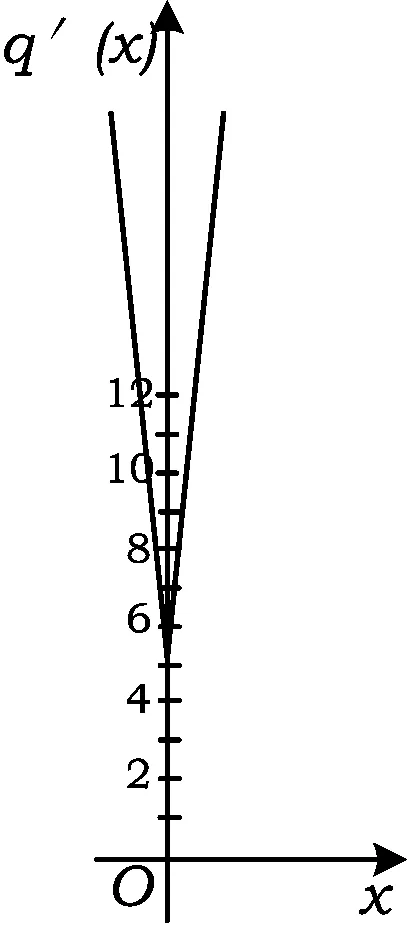
注根據極大值的含義，由題設中“x=a是f(x)的一個極大值點”，可知在x=a的某個鄰域內的任意一個x的值，均有f(x)

“數學味”源自何處？到底是什么能令人擊節贊賞，頓覺眼前一亮？以蘊涵于試題背后的學科本質及數學思想的高立意為支撐設計的試題就有這樣的神奇.

2 看一看，圖像直觀本質顯

華羅庚先生曾言：“數缺形時少直觀，形少數時難入微，數形結合百般好，隔裂分家萬事休.”利用圖像的直觀性解題是重要的思考方法之一，體現了數形結合的數學思想.函數圖像不止是直觀地反映了函數的性質，而且能充分簡化思維的過程，體現問題的本質.如例2的解決就充分利用了圖像的直觀性.

例3已知函數f(x)=x3-(k2-k+1)x2+5x-2，g(x)=k2x2+kx+1，其中x∈R.

(1)略；

(2009年浙江省數學高考理科試題)

注當x<0時,

q′(x)=f′(x)=

3x2-2(k2-k+1)x+5；

當x>0時,

q′(x)=g′(x)=2k2x+k.

圖6

因為當k=0時不合題意，因此k≠0，q′(x)的圖像左側為二次函數一部分，右側為一次函數一部分.由題意，結合圖像(圖6)可知k=5滿足題意．圖像的直觀性使問題顯得自然和諧，解答思路簡潔明快，充分體現了數形結合的魅力.

再如，2012年理科第9題將函數圖像與不等式問題進行了巧妙的結合，通過畫圖答案一目了然.這樣的試題在歷年的浙江卷中比比皆是，理由很簡單：此類試題既能深層次地考查函數的性質，又能充分考查數形結合思想.

3 選一選，方法多樣數感聯

高考試題具有豐富的內涵，因此其解決的方法也具有多樣性，從不同的角度切入，就會有不同的發現，而這些方法的背后聳立著數學思想的豐碑.如何選擇合適的方法，和學生平時對各種方法的熟悉程度有關，在一定意義上考查了學生對數學解題的感覺.

例4設x,y為實數，若4x2+y2+xy=1,則2x+y的最大值是______.

(2011年浙江省數學高考理科試題)

注此題解法眾多，也引發了一些較為深入的研究.筆者簡單羅列了一下，至少可以寫出13種解法，比如判別式法、不等式、參數方程、換元法、向量法、函數法等等.各種方法是有繁簡之別的，但其背后都有著數學思想的支撐.這其實也是我們平常教學的好素材.

4 導一導，二次函數威風見

導數是解決函數單調性問題的重要工具，而二次函數的考查是數學高考的永恒主題，“3個二次”的問題值得細細研究，牢牢掌握.

例5已知函數f(x)=x3-(k2-k+1)x2+5x-2，g(x)=k2x2+kx+1，其中k∈R.設函數p(x)=f(x)+g(x),若p(x)在區間(0,3)上不單調，求k的取值范圍.

(2009年浙江省數學高考理科試題)

注將“p(x)在區間(0,3)上不單調”轉化為“p′(x)=0在(0,3)上有實數解，且無重根”，問題即轉化為二次函數問題(或二次方程根的存在問題，即“3個二次”的問題).結合圖像，或直接根據二次函數的圖像分類，或利用參變分離加以轉化，都可以解決此題.

例6已知a>0,b∈R，函數f(x)=4ax3-2bx-a+b.

(1)證明：當0≤x≤1時，①函數f(x)的最大值為|2a-b|+a；②f(x)+|2a-b|+a≥0.

(2)若-1≤f(x)≤1對x∈[0,1]恒成立，求a+b的取值范圍.

注第(1)小題第①問利用導數求函數的單調性，并利用二次函數的性質(開口向上的二次函數在閉區間上的最大值只能是端點值)得到

f(x)max= max{f(0),f(1)}=

max{-a+b,3a-b}，

然后利用要證明的結論明確分類標準并合并.此題看上去并不難，但不熟悉二次函數最值性質的學生可能會將這個問題復雜化，即增加分類.第(1)小題第②問將2類情況中f(x)+|2a-b|+a統一縮小為2a(2x3-2x+1)并進而通過求導轉化為二次函數問題.此問也可不化歸為統一函數而直接用分類討論解決，但過程繁冗.此題的特點:思考的力量遠高于具體的運算，其涉及函數與方程、分類與整合、數形結合、化歸與轉化等基本數學思想．

再如，2012年數學高考理科第16題通過新定義問題，利用導數求切線或利用配方法求二次函數的最值，以解析幾何為載體考查函數問題；理科第21題利用二次函數性質求最值的問題等等．

通過以上分析可以看到：浙江卷中的函數問題是高考的重點和難點，是命題者精心設計試題的著眼點．其注重對數學思想的深入考查;注重數學本質的理性挖掘；注重圖像的演繹，通過圖像可以快捷地解決那些難度較大的把關題；注重二次函數的考查，“3個二次”在函數問題中比比皆是．因此，在高三復習教學中，依靠“題型+技巧+大運動量訓練”的教學難以適應高考，只有突出數學本質、實現高中數學教學的自然回歸才是復習的方向.具體而言：

(1)作為函數復習，應更多地關注函數本身的性質，關注函數圖像.遇到函數問題，多讓學生嘗試畫圖，用圖像來思考和解決問題，當然，這其中有一些工具不可或缺，如導數等．

(2)關于導數，必須明確的是導數只是研究函數單調性和極值的工具，過多地關注導數處理問題的技巧是本末倒置．

(3)“3個二次”的問題是浙江卷考試的重點也是難點，在復習中要引起充分重視，要不斷挖掘其中的變化，讓學生通過諸多的變式深刻體會二次函數的本質以及衍生出的種種問題.

(4)數學思想是數學學習的靈魂，對其的滲透非一朝一夕之功，需要教師通過各種問題有意識地加以培養，變隱形的思想為顯性的方法，變抽象的理念為具體的策略，以期讓學生能自覺地加以運用．