關于理想氣體混合熵變的討論

岳凡 陳華梅 孫都成

(新疆大學化學化工學院 新疆烏魯木齊 830046)

物理化學是大學化學專業學生必修的四大專業基礎課之一，而化學熱力學則是物理化學中非常重要的內容之一。化學熱力學理論性強，數學處理比較復雜，公式較多，而且公式的使用限制條件也較多，學生不易掌握。因此，在物理化學教學中，可盡量通過比較形象化的方式使學生理解，并適當地將理論與實際相聯系，使學生體會到學習物理化學的樂趣，從而達到在有限的教學課時內使學生對本課程內容更好掌握的目的[1]。

在文獻[2]第3章第87～88頁中，討論了理想氣體的等溫等容混合熵變，這是一個比較容易出錯和容易混淆的概念。

原文提出，對于相同理想氣體的等溫等容混合，如圖1所示。

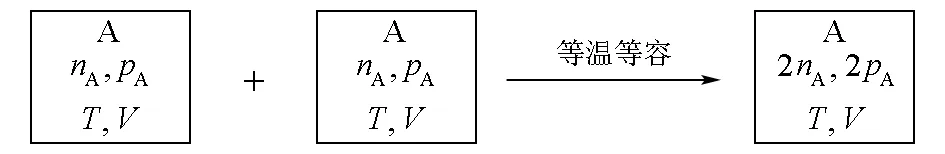
圖1 相同理想氣體等溫等容混合

由于是相同分子的混合，每個分子在混合后的活動范圍縮小一半，相當于體積縮小一半，氣體被壓縮，所以混合后熵減少，其熵變為：

不同理想氣體的等溫等容混合如圖2所示。

圖2 不同理想氣體等溫等容混合

因為是理想氣體的等溫物理變化過程，所以ΔmixU=0。終態壓力p=pA+pB，有：

Δ(pV)=pV-(pAV+pBV)=0

所以有：

ΔmixH=ΔmixU+Δ(pV)=0

對于不做非膨脹功的等容可逆過程，QR=ΔmixU=0，所以

ΔmixS=0

因為是不同理想氣體的混合，根據理想氣體的微觀模型，氣體分子之間的相互作用力可以忽略不計，分子本身的體積也可以忽略，所以混合前后兩種不同分子的活動范圍都沒有發生變化，混合時沒有熱效應，所以也就沒有熵的變化。

關于這點，學生學習時會感到很迷惑，其一是，書中對第二種情況推導所得的ΔmixU=0以及ΔmixH=0在對第一種情況似乎同樣適用，當然這一步事實上是正確的。那么問題就在下一步，“對于不做非膨脹功的等容可逆過程，QR=ΔmixU=0，所以ΔmixS=0。”這段話，應該只適用于第二種情況，而對相同氣體的這一過程來說，這段話并不適用，學生對于這一點有疑義，由于這種懷疑心理而產生的不確定感，導致學生認為物理化學課程學習有些不可掌握，從而產生一定程度的陌生感及厭學情緒。為克服學生的這些負面感覺，在教學過程中可采用學生較熟悉的推導過程來證明這一結論；另外，由于形象化教學更易理解，更易記憶，在教學過程中也被嘗試采用。

首先，用學生比較熟悉的兩個過程來模擬這一過程，從而證明這一結論的正確性。

對于相同的理想氣體，先設計第一步，將兩等壓等體積的相同理想氣體，經一等溫等壓過程，合并為兩體積的理想氣體，如圖3所示。

圖3 相同理想氣體等溫等壓混合

學生很容易從這一過程得出熵變為0的結論。

第二步，將這一氣體等溫壓縮至體積為原來的一半，即上述過程的終態。在這一過程中，由于是等溫變化，所以ΔU=0，QR=-WR。對于等溫可逆過程，有：

所以有：

與課本結果相同。

對于不相同的理想氣體，也經過同一過程(圖4)。

圖4 不同理想氣體等溫等壓混合

在第一步時，由于是不同氣體發生混合，則混合熵可根據前面第2節的結論，得計算結果為：

然后將這一混合氣體等溫壓縮為原來的一半，這時，根據與上面同樣的理由，可得此時的熵變為：

將兩式相加，可得這一過程的總熵變為0。

通過以上過程的證明，一方面使學生對該問題有了可掌握感，另一方面，也是對以前教學內容的一種復習鞏固。

另外，為形象地解釋這種熵變產生的原因，可由熵的玻爾茲曼定義[2]S=klnΩ(Ω為微觀狀態數)對這一過程進行討論。

在相同氣體分子進行混合時，為簡化討論，將其設為一個小球在兩個格子里的排列，對于兩體積氣體混合前后的過程，可以簡化表示如圖5。

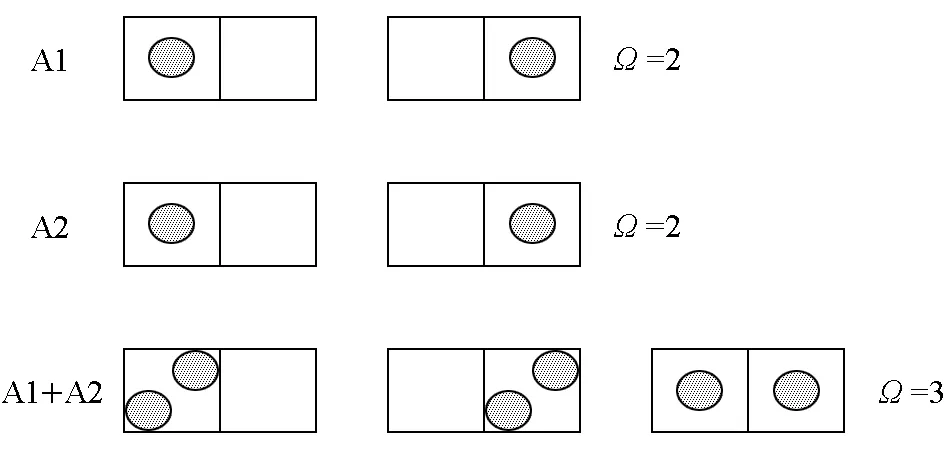
圖5 相同理想氣體等溫等容混合簡化統計表達

此時總的微觀狀態數為3，小于前兩者分開時總的微觀狀態數4。經觀察之后，學生可發現，在A1+A2狀態時，第3種狀態由于A1與A2的不可區分性，由兩種狀態變成了一種狀態，就是由于這一原因，造成同一理想氣體在等溫混合時產生了熵減。

對于不同理想氣體等溫等容混合時，其統計學圖像簡化如圖6。此時，混合前后微觀狀態數不變。

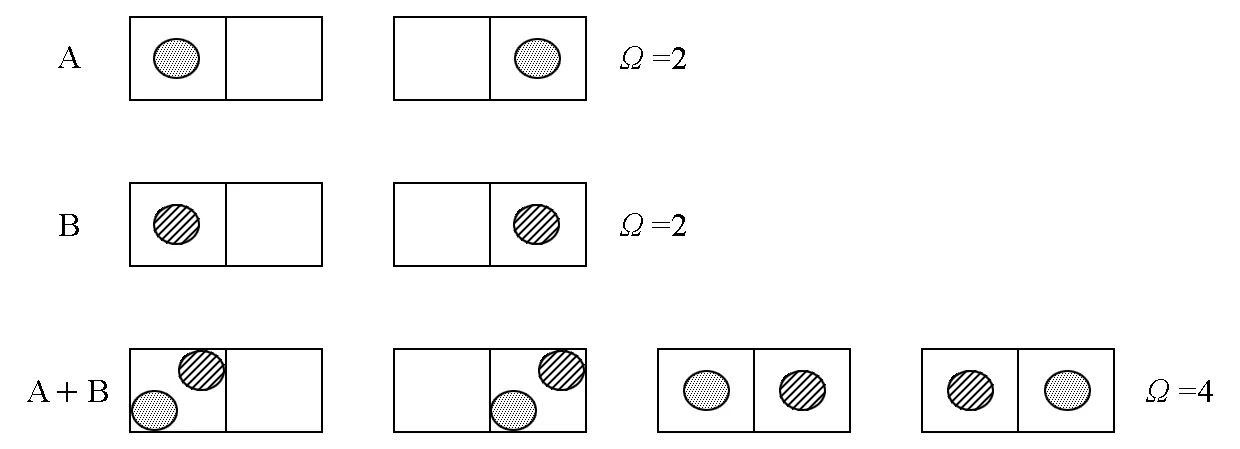
圖6 不同理想氣體等溫等容混合簡化統計表達

從統計角度可清楚地揭示兩種混合狀態物理圖像的差別。在A+B中，第3種狀態與第4種狀態是不同的，表明此時A在左與A在右有區別，就好像A+B之后，A仍然獨立地占有兩個格子；所以，對于A來說，這是一個等容過程。而在A1+A2中，這兩種狀態變成不可區分的一個狀態，此時A1在左與A1在右沒有區別，就好像A1+A2后，A1只占據其中一個格子一樣；所以，對于A1來說，這是一個體積減小了一半的非等容過程。

問題討論到此，學生還有一個疑問，就是關于這個問題的熱力學解釋的實際意義。如果不能應用于解決實際問題，就純粹是一個抽象的理論游戲，這樣學生就缺乏掌握此概念的動力，認為這是一個既麻煩，又無用的章節。下面采用一個在化工生產中非常重要的反應來進行說明。

對于這個反應來說，達到平衡時，有如下關系：

ΔrG=ΔrH-TΔrS=0

對此體系加入一惰性氣體，使總壓增加一倍，而體積保持不變。這就相當于上面討論的不同理想氣體等溫等容混合。因為是理想氣體等溫混合過程，所以沒有混合熱，此反應的ΔrH不變。對于O2(g)及CO(g)來說，由上面結論可知，兩物質的熵也不改變，所以ΔrG仍然等于0，平衡不發生改變，與用平衡常數討論的結果相同。而當加入反應氣體時，由于混合熵改變，將導致反應平衡被打破。

通過以上討論，能使學生從多個角度來理解理想氣體混合熵變這一過程，使抽象的問題具體化。通過該教學設計，不但不會加重學生的負擔，反而會提高學生對不同過程熵變的計算及其推論的理解，在介紹新概念的同時，達到復習舊課程、提高記憶準確性的目的。在實施新課改的今天，我們讓學生從不同的角度認識和解決同一類問題，有利于培養學生分析問題和解決問題的能力，提高學習效果。

參 考 文 獻

[1] 劉瑞泉,張金萍.烏魯木齊成人教育學院學報,1997(2):54

[2] 沈文霞.物理化學核心教程.第2版,北京:科學出版社,2009