基于局部均值分解與形態學分形維數的滾動軸承故障診斷方法

張 亢，程軍圣，楊 宇

(湖南大學 汽車車身先進設計制造國家重點實驗室，長沙 410082)

滾動軸承系統因受間隙、動載荷、非線性接觸力、剛度非線性等因素影響，常表現出較強非線性特征［1-2］，而該特征隨系統狀態、所受非線性因素影響的不同會有所不同。因此，若能準確描述滾動軸承系統在不同狀態下的非線性行為，對正確區分滾動軸承工作狀態與故障類型非常有意義［3］。事實上，滾動軸承系統非線性特征一般會反映在振動信號中，即其非線性特征不同時，振動信號會呈現不同的幾何形狀，且系統非線性程度越嚴重，振動信號幾何形狀會越復雜無規律。因此，通過對滾動軸承振動信號幾何特征進行分析描述其非線性行為理論上是可行的。“分形”可描述自然界中用傳統歐幾里得幾何不能描述的復雜無規律的幾何對象，而分形維數是度量分形的重要參數，可定量描述被分析對象的復雜度及非線性程度，故可對滾動軸承振動信號進行分形分析，用分形維數判斷滾動軸承系統工作狀態。

目前已有多種分形維數，已在振動信號分析方面關聯維數與盒維數中廣泛應用［4-8］。分形維數估計一般基于不同尺度下對分形集，即不規則幾何形狀集合進行度量的基本思想。與多尺度形態學在不同尺度下對被分析對象的幾何形態進行度量思想一致。因此Minkowski等提出利用多尺度形態學算子估計信號分形維數方法。Maragos等［9］從提高計算效率角度對該方法進行改進及優化。與其它分形維數估計方法相比，基于形態學的分形維數估計方法具有計算復雜度低、計算結果穩定性好等優點，且對信號幾何形態變化反應敏感。對滾動軸承振動信號，若系統狀態發生改變其幾何形態必然也會發生變化，因此可通過估計滾動軸承振動信號形態學分形維數判斷其工作狀態。然而，實測的滾動軸承系統原始振動信號往往含有大量噪聲成分，因實際隨機噪聲不存在嚴格的分形［10］，直接計算原始振動信號的形態學分形維數結果不可靠。為得到精確的形態學分形維數，須先對滾動軸承振動信號進行降噪處理。局部均值分解(Local Mean Decomposition，LMD)［11］方法為非平穩、非線性信號分析方法，能自適應地將信號分解為一系列乘積函數(Product Function，PF)分量，每個PF分量均代表原信號特征尺度成分。若能利用LMD方法對滾動軸承振動信號進行分解，得到若干PF分量，舍棄噪聲分量，只保留含故障特征信息的PF分量，并計算PF分量的形態學分形維數，能提高形態學分形維數的精確度，從而能更準確判斷滾動軸承系統工作狀態及故障類型。因此，本文提出基于LMD及形態學分形維數的滾動軸承故障診斷方法，對滾動軸承實驗信號分析結果表明，該方法能準確識別滾動軸承工作狀態及故障類型，為有效的滾動軸承故障診斷方法。

1 形態學分形維數估計

1.1 算法

分形維數能在不同尺度下度量分形集邊界復雜度與不規則度，是對分形集進行描述與分類的重要特征量。因振動信號的拓撲維為一維，故此處只討論拓撲維為一維的實數數據序列分形維數。分形維數有多種定義方式，其中基于“覆蓋”思想的定義方式原理清晰且便于計算，具體為:設X為實平面集R2中的一個非空子集，b為實平面集R2中一個尺度為ε的閉集，若覆蓋集合X所需閉集b的數目為N(ε)，則可定義集合X的分形維數D為:

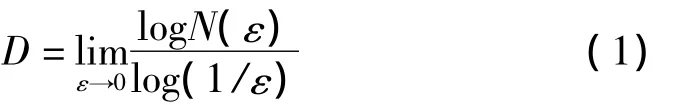
由式(1)可知，估計分形維數過程實際為在不同尺度下對分形集進行度量的過程，而如何實現該不同尺度下對分形集的度量為估計分形維數關鍵。

多尺度形態學為在不同尺度下對信號形態特征進行度量的數學方法。因此可利用多尺度形態學估計信號的分形維數。Minkowski為計算不規則曲線長度，提出Minkowski覆蓋法，即利用不同尺度圓盤形結構元素對曲線進行膨脹運算，以實現對曲線的覆蓋;Bouligand將該覆蓋法中圓盤形結構元素推廣到任意形狀的平面形結構元素，提出估計一維信號分形維數方法，并稱為Minkowski-Bouligand維數DM。由于計算DM時采用二維平面形結構元素，因此具有二次方的計算復雜度。為降低計算復雜度，提高計算效率，Maragos等提出另一種方法估計信號的Minkowski-Bouligand維數。該方法同樣基于多尺度形態學，其理論基礎為:對一維信號分形維數的估計，認為平面集B覆蓋一維信號方式與采用一維函數g對信號進行形態學變換方式等效，其中一維函數g為平面集B的上確界［9］。對一維離散時間信號f(n)，(n=0，1，…，N)，該方法具體算法為:

(1)設B為關于x，y軸對稱、單連通的實平面集，g(n)為平面集B的上確界，取 ε =1，2，…，εmax為分析尺度范圍，在每個尺度ε下將一維離散函數g(n)作為單位結構元素對f(n)進行一次膨脹及腐蝕運算，即:

(2)在形態學中對信號進行膨脹及腐蝕運算，即對信號求上、下包絡。由此可定義在尺度ε下信號f(n)關于結構元素g(n)膨脹及腐蝕運算的覆蓋面積Ag(ε)為:

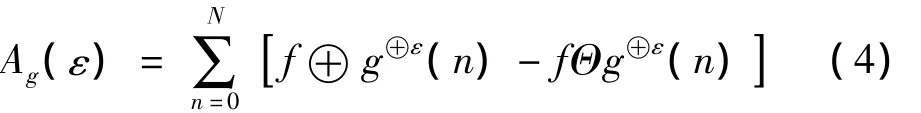
(3)Maragos證明當 ε→0時，Ag(ε)的成立等式為:

其中:DM為信號 Minkowski-Bouligand維數，ε'?2ε/N為歸一化尺度。因此只需對log(Ag(ε)/(ε')2)和log(1/ε')進行最小二乘線性擬合即能得到一條直線，該直線斜率即為信號f(n)的Minkowski-Bouligand維數。

上述估計Minkowski-Bouligand維數算法只用一維結構元素，故計算復雜度是線性的，可大大提高計算效率。然而，用該算法估計信號Minkowski-Bouligand維數，對單位結構元素選擇是有限制的。由于:① 平面集B須關于x，y軸對稱且單連通;② 為獲得精確估計結果，平面集B須具盡量小尺度，平面集B的形狀只能是以坐標原點為中心的3×3個點正方形、5個點菱形或3個點水平線段，致使B的上確界，即單位結構元素g(n)只能定義在n=-1，0，1 上的h×{1，1，1}、h×{0，1，0}或{0，0，0}，其中h為高度參數。當單位結構元素為{0，0，0}時，算法可減少部分計算量且維數估計結果不會受信號幅值范圍影響，故本文選{0，0，0}作為單位結構元素。對最大分析尺度取εmax=N/2，即分析尺度范圍為1≤ε≤N/2，其中ε為正整數。

1.2 仿真信號分析

為驗證估計分形維數的準確度對人造分形信號進行分析。魏爾斯特拉斯余弦函數(Weierstrass Cosine Function，WCF)為參數化分形測試信號，定義為:

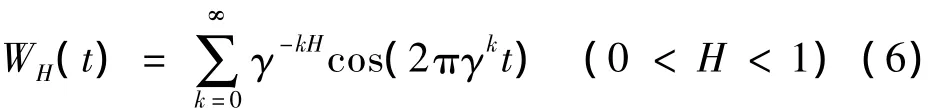
其中:γ＞1，理論上WH(t)的分形維數為D=2-H。式(6)為WH(t)的連續形式，具體分析時可設采樣時長1 s、采樣頻率1 000 Hz對WH(t)進行離散。另取γ=5，0≤k≤20。圖1、圖 2 分別為分形維數D=1.5、D=1.8 時，即W0.5(t)、W0.2(t)的時域波形，由圖看出，W0.2(t)較W0.5(t)波形更破碎。采用基于形態學的分形維數估計方法估計兩者分形維數，尺度ε分別為10、20時W0.5(t)關于結構元素g(n)的膨脹及腐蝕運算結果(截取0.3～0.7 s時間段波形)見圖3，可以看出，實際上為對W0.5(t)進行不同尺度的包絡。W0.5(t)的雙對數見圖4，圖中直線斜率K=1.518 2即W0.5(t)的分形維數。同樣可得W0.2(t)的分形維數為1.791 3，與理論值誤差分別為1.82%，0.87%，說明基于形態學的分形維數估計方法準確度較高。產生誤差的主要原因為k的取值范圍從無限變成有限及信號離散誤差。

盒維數為常用分形維數估計方法，與形態學分形維數相同，亦通過“覆蓋”方式估計信號分形維數。便于對比，采用盒維數計算方法估計W0.5(t)，W0.2(t)分形維數結果分別為1.386 0，1.617 9，與理論值誤差分別為11.40%，18.21%。故盒維數計算方法的估計精度較形態學分形維數估計精度差。

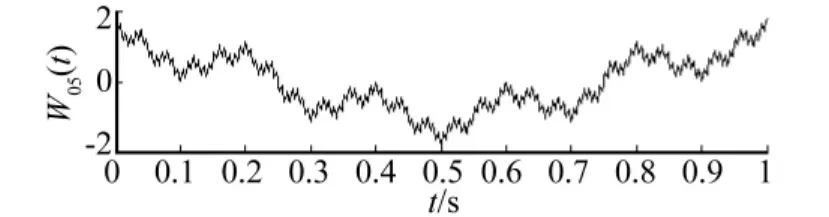
圖1 魏爾斯特拉斯余弦函數w0.5(t)Fig.1 Weierstrass cosine function w0.5(t)

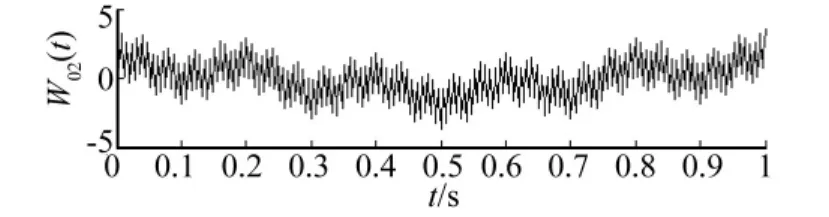
圖2 魏爾斯特拉斯余弦函數w0.2(t)Fig.2 Weierstrass cosine function w0.2(t)

圖3 w0.5(t)膨脹及腐蝕運算結果Fig.3 Results of dilation and erosion for w0.5(t)

圖 4 w0.5(t)雙對數圖Fig.4 Log-log graph for w0.5(t)

2 基于LMD及形態學分形維數的滾動軸承故障診斷方法

2.1 方法原理

形態學分形維數計算結果與其它分形維數計算結果一樣均會受噪聲影響，而實測的滾動軸承振動信號或早期故障信號通常含有大量背景噪聲，能反映軸承系統狀態的特征成分常被噪聲湮沒，直接影響到形態學分形維數的準確性。因此，通過形態學維數判斷滾動軸承系統的工作狀態，須先對原始滾動軸承故障振動信號進行降噪處理。采用新的自適應非平穩、非線性信號分解(LMD)方法，可將任意復雜信號自適應地分解為若干PF分量和，每個PF分量代表原信號一種特征成分，將滾動軸承振動信號中的狀態特征成分從噪聲等干擾成分中分離出來。與類似經驗模態分解(Empirical Mode Decomposition，EMD)［12］方法相比，LMD方法具有迭代次數少、端點效應不明顯、瞬時頻率無負值等優點［13］。本文將LMD方法與形態學分形維數相結合，提出基于LMD與形態學分形維數的滾動軸承故障診斷方法，具體步驟為:① 采用LMD方法對原始滾動軸承振動信號進行分解，得到若干個PF分量［11］。② 據滾動軸承發生故障時的故障機理及實際工況，選出含故障特征的PF分量，并舍棄噪聲分量及不具代表性的PF分量。③ 利用計算選取的PF分量形態學分形維數判斷滾動軸承系統的工作狀態及故障類型。

2.2 應用

在旋轉機械實驗臺上分別進行滾動軸承內圈故障、外圈故障及正常狀態實驗。軸承型號SKF6307，軸轉速680 r/min，采樣頻率8 192 Hz，每種狀態下各采集9組數據。圖5、圖6、圖7分別為軸承正常、內圈故障及外圈故障狀態下某一組數據的時域波形，可以看出軸承正常狀態振動信號振幅較小，表現為隨機噪聲特征;內、外圈故障狀態的振動信號振幅較大，且存在故障性沖擊特征，較難通過時域波形進行區分。采用基于形態學的分形維數估計方法直接計算各狀態原始振動信號的分形維數，結果見圖8，可以看出正常狀態下振動信號的分形維數較大，且與故障狀態下振動信號分形維數區分明顯;內、外圈故障狀態下振動信號的分形維數較小，且差別較小，無法區分。原因為正常狀態的振動信號接近隨機噪聲，形態最復雜無規律，分形維數較大，兩種故障狀態的振動信號由于存在故障性沖擊成分，形態具有一定確定性及規律性，分形維數較小;另外，因兩種故障狀態的振動信號中均存在相似的背景噪聲，形態上也具有相似性，故分形維數較接近，無法區分滾動軸承的故障類型。

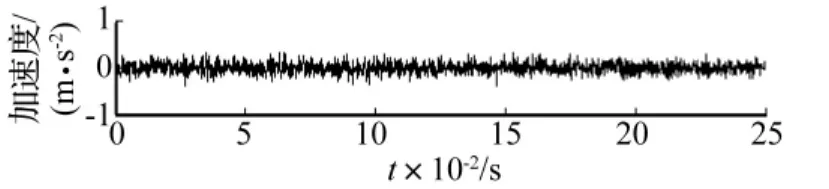
圖5 滾動軸承正常狀態振動加速度信號g.5 Vibration acceleration signal of norm roller bearings

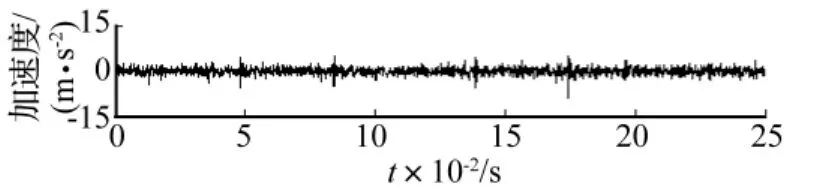
圖6 滾動軸承內圈故障狀態振動加速度信號Fig.6 Vibration acceleration signal of roller bearings with inner race defect

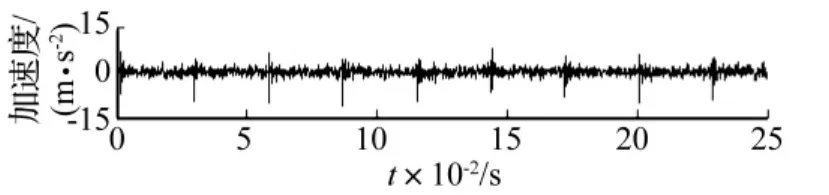
圖7 滾動軸承外圈故障狀態振動加速度信號Fig.7 Vibration acceleration signal of roller bearings with outer race defect

圖8 滾動軸承各狀態振動加速度信號形態學分形維數(△:正常狀態，*:內圈故障，O:外圈故障)Fig.8 The morphological fractal dimensions of vibration acceleration signal of roller bearings

采用LMD方法將滾動軸承原始振動信號由高頻至低頻分解為若干個PF分量，因含故障特征信息的固有振動成分屬高頻成分，因此只需計算分解所得第1個PF分量的分形維數，便可準確識別出滾動軸承工作狀態。圖9～圖11分別為圖5～圖7所示信號的第1個PF分量PF1(t)，對比看出，正常狀態下PF1(t)與原始振動信號波形差別不大，內、外圈故障狀態下PF1(t)的沖擊特征明顯加強，信噪比得以提高。采用基于形態學的分形維數估計方法計算3種狀態下所有27組數據第1個PF分量的分形維數D，結果見圖12，可看出，此時分形維數D能清晰將滾動軸承3種狀態區分開，雖因隨機噪聲不存在嚴格分形造成正常狀態的分形維數出現較大波動，但并不影響對滾動軸承各狀態的正確區分。由此表明基于LMD的形態學分形維數能有效應用于滾動軸承的故障診斷。

為便于對比，將LMD與盒維數結合對測試樣本進行分析，樣本數據及序號與上述一致，計算結果見圖13，可以看出，正常狀態與內圈故障狀態的盒維數結果部分有重疊，無法區分，且3種狀態的盒維數結果動態范圍無形態學分形維數大，說明形態學分形維數具優越性。

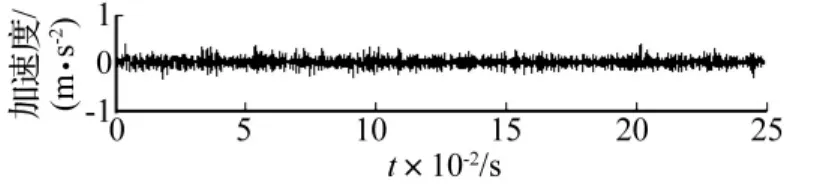
圖9 滾動軸承正常狀態振動信號第1個PF分量Fig.9 The 1st PF of norm roller bearings vibration signal

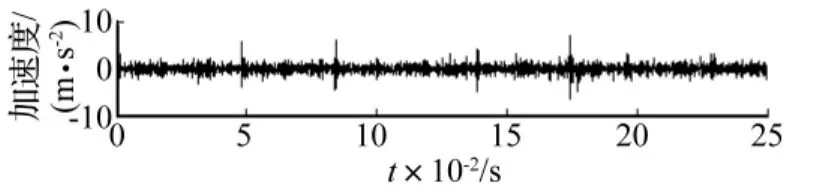
圖10 滾動軸承內圈故障狀態振動信號第1個PF分量Fig.10 The 1st PF of roller bearings vibration signal with inner race defect

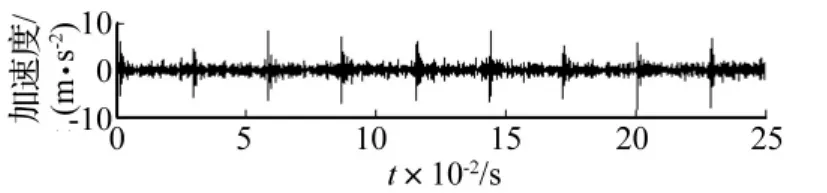
圖11 滾動軸承外圈故障狀態振動信號第1個PF分量Fig.11 The 1st PF of roller bearings vibration signal with outer race defect

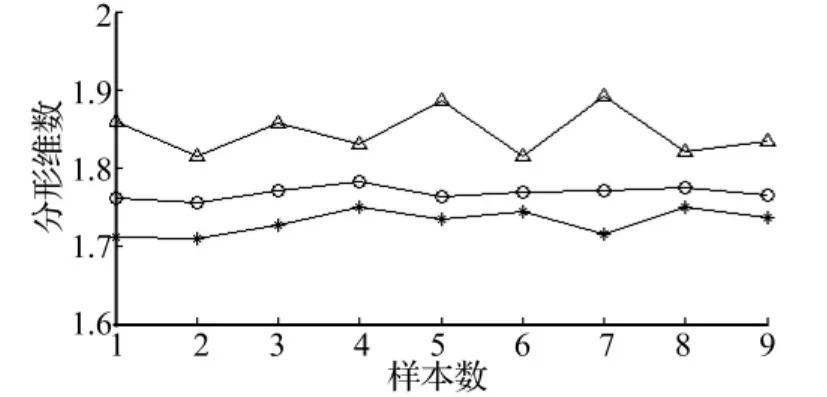
圖12 特征PF分量的形態學分形維數(△:正常狀態，*:內圈故障，O:外圈故障)Fig.12 The morphological fractal dimensions of characteristic PF

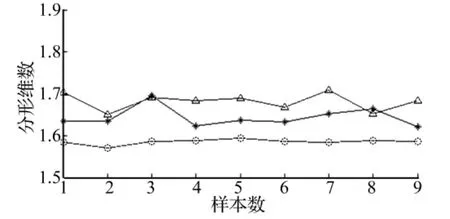
圖13 特征PF分量的盒維數(△:正常狀態，*:內圈故障，O:外圈故障)Fig.13 The box counting dimensions of characteristic PF

3 結論

(1)通過形態學運算估計信號分形維數具有原理直觀簡單、計算效率高等特點，對仿真分形測試信號分析結果表明，形態學分形維數估計精度較高。

(2)LMD方法能將滾動軸承振動信號中的特征成分與噪聲等干擾成分分離，可提高信號的信噪比。

(3)將LMD與形態學分形維數結合，提出基于LMD與形態學分形維數的滾動軸承故障診斷方法，通過對滾動軸承故障實驗信號分析，表明該方法可準確地判斷滾動軸承的工作狀態及故障類型，為滾動軸承故障診斷提供了新的有效途徑。

［1］陳 果.滾動軸承支撐下的不平衡轉子系統非線性動力響應分析［J］.中國機械工程，2007，18(23):2773-2778.

CHEN Guo.Nonlinear dynamic response analysis of an unbalanced rotor supported on ball bearing［J］.Chinese Mechanical Engineering，2007，18(23):2773-2778.

［2］張耀強，陳建軍，唐六丁，等.考慮外圈局部缺陷的滾動軸承非線性動力特性［J］.航空學報，2009，30(4):751-756.

ZHANG Yao-qiang，CHEN Jian-jun，TANG Liu-ding，et al.Nonlinear dynamic characteristics of rolling element bearing with localized defect on outer ring［J］.Acta Aeronautica ET Astronautica Sinica，2009，30(4):751-756.

［3］呂志民，徐金梧，翟緒圣.分形維數及其在滾動軸承故障診斷中的應用［J］.機械工程學報，1999，35(2):87-90.

Lü Zhi-min，XU Jin-wu，ZHAI Xu-sheng.Fractal dimension and its application in fault diagnosis of rolling bearing［J］.Journal of Mechanical Engineering，1999，35(2):87-90.

［4］楊文平，陳國定，石博強，等.基于分形理論的斯太爾汽車發動機故障診斷的研究［J］.機械工程學報，2002，38(2):49-52.

YANG Wen-ping，CHEN Guo-ding，SHI Bo-qiang，et al.Based on fractal theory for steyr diesel engines diagnosis［J］.Journal of Mechanical Engineering，2002，38(2):49-52.

［5］汪慰軍，陳 進，吳昭同.關聯維數在大型旋轉機械故障診斷中的應用［J］.振動工程學報，2000，13(2):229-234.

WANG Wei-jun，CHEN Jin，WU Zhao-tong.Application of correlation dimension in fault diagnosis for large rotating machinery［J］.Journal of Vibration Engineering，2000，13(2):229-234.

［6］李 琳，張永祥，明廷濤.EMD降噪的關聯維數在齒輪故障診斷中的應用研究［J］.振動與沖擊，2009，28(4):145-148.

LI Lin，ZHANG Yong-xiang，MING Ting-tao.Gear fault diagnosis based on correlation dimension pre-processed with EMD［J］.Journal of Vibration and Shock，2009，28(4):145-148.

［7］郝 研，王太勇，萬 劍，等.分形盒維數抗噪研究及其在故障診斷中的應用［J］.儀器儀表學報，2011，32(3):540-545.

HAO Yan，WANG Tai-yong，WAN Jian，et al.Research on fractalbox dimension anti-noise performance and its application in faultdiagnosis［J］. ChineseJournalof Scientific Instrument，2011，32(3):540-545.

［8］樊福梅，梁 平，吳庚申.基于分形盒維數的汽輪機轉子振動故障診斷的實驗研究［J］.核動力工程，2006，27(1):85-89.

FAN Fu-mei，LIANG Ping，WU Geng-shen.Experimental research on steam-turbine rotor vibration fault diagnosis based on the fractal box counting dimension［J］.Nuclear Power Engineering，2006，27(1):85-89.

［9］Maragos P，Sun F K.Measuring the fractal dimension of signals:morphological covers and iterative optimization［J］.IEEE Transactions on Signal Processing，1993，41(1):108-121.

［10］張濟忠.分形［M］.北京:清華大學出版社，1995.

［11］ Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2(5):443-454.

［12］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proc.R.Soc.Lond.A，1998，454(1971):903-995.

［13］程軍圣，張 亢，楊 宇，等.局部均值分解與經驗模式分解的對比研究［J］.振動與沖擊，2009，28(5):13-16.

CHENG Jun-sheng， ZHANG Kang， YANG Yu， et al.Comparison between the methods of local mean decomposition and the empirical mode decomposition［J］.Journal of Vibration and Shock，2009，28(5):13-16.