3種確定性采樣非線性濾波算法的復雜度分析

張召友，郝燕玲，吳 旭

(哈爾濱工程大學自動化學院，150001哈爾濱)

卡爾曼濾波是實現捷聯慣性導航系統(strapdown inertial navigation system，SINS)和全球定位系統(global positioning system，GPS)組合導航數據融合的首選方法［1-2］.低精度傳感器構成的組合系統在復雜應用環境中易產生大的誤差，導致系統非線性度增加，此時線性卡爾曼濾波已不再適用，而擴展卡爾曼濾波(extended Kalman filter，EKF)也難以保證系統性能.隨著近年非線性濾波的快速發展，較EKF精度更高的確定性采樣卡爾曼濾波被用于處理組合導航中的非線性融合問題.確定性采樣卡爾曼濾波是一類利用有限固定采樣點對高斯系統中狀態的一二階矩進行近似，并經過非線性函數傳播后進行加權求和估計的濾波算法.最為常用的3種確定性采樣算法為［3］無跡卡爾曼濾波(unscented Kalman filter，UKF)、中心差分卡爾曼濾波(central difference Kalman filter，CDKF)、容積卡爾曼濾波(cubature Kalman filter，CKF)算法.

精度是表征濾波性能的重要指標，大量文獻已證實UKF、CDKF、CKF的精度相當，均至少可達二階［4-5］.但在導航系統中，濾波多是在嵌入式計算機中實現，因此復雜度是影響其應用的另一個重要參數.先前對于非線性濾波復雜度的研究多是對單一算法的改進與分析［6-8］，對于形式相近的確定性采樣算法之間缺乏系統的分析與比較.因此，本文將對3種典型確定性采樣算法進行等效復雜度的理論分析，導出定量的計算表達式，并進行橫向比較，得出算法實時性選擇的依據.最后，將確定性采樣算法應用于SINS/GPS的緊耦合組合導航，對其精度和復雜度進行仿真，驗證分析的正確性.

1 確定性采樣濾波的等效復雜度分析

濾波的精度是保證系統性能的前提，但當精度滿足要求后濾波的易實現性與否是另一個制約因素，復雜度是表征易實現性的主要參數.本節將對UKF、CDKF、CKF的復雜度及差異進行分析，力圖得出一個精確的、定量的表述.

1.1 確定性采樣濾波中數值運算的復雜度

分析算法復雜度最為有效的方法是對其浮點操作數(flops)的準確統計.一次flops定義為兩個浮點數進行一次加、減、乘或除法運算.但濾波中的很多運算難以用加、減、乘、除來簡單描述，如開方、數值分解、指數運算等，因此只能將其等效為相同運行時間的flops，故稱為等效復雜度分析.本文給出濾波中基本代數運算的flops次數［1］:1)矩陣加減法.A∈Rn×m，B∈Rn×m，計算A±B需nm次flops.2)矩陣相乘.A∈Rn×m，B∈Rm×l，計算AB的flops為2mnl-nl次.3)矩陣求逆.A∈Rn×n，A-1的flops數為n3.4)Cholesky分解.A∈Rn×n，則chol(A)需要進行n3次flops.

利用上述諸元素即可對確定性采樣卡爾曼濾波進行復雜度的分析.

1.2 確定性采樣濾波的等效復雜度分析

3種確定性采樣算法的濾波形式相近，均包括樣本點產生、基于狀態方程與量測方程的均值與方差預測以及狀態與方差的后驗估計等步驟.算法實現形式均為加性噪聲形式，UKF與CDKF的詳細公式參見文獻［4］，CKF的公式參見文獻［5］.按照濾波過程可對相應算法進行分析.由于具體的分析過程較為繁瑣，在此只給出CKF算法的分析過程如下.

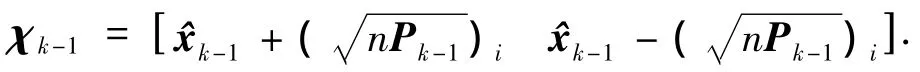
狀態方程預測，如下式，獲得樣本點預測χk｜k-1需要4n3-2n2次flops(3種算法均以線性矩陣形式代換)，獲得狀態預測值1需要2n2次flops，預測協方差Pk｜k-1需要 2n3+4n2次 flops.

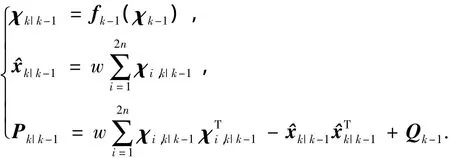
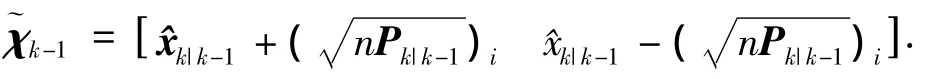
量測方程預測，如下式，獲得樣本點預測γk｜k-1需要 4n2l-2nl次 flops，獲得量測預測值yk｜k-1需要2nl次flops，預測量測協方差Pyk需要4nl2+3l2次flops，互協方差Pxkyk需要4n2l+2nl次flops.

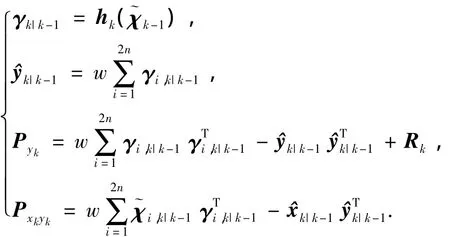
計算后驗估計，如下式，增益Kk需l3+(2nl2-nl)次flops，協方差更新Pk需要2nl2-nl+2n2l次flops，狀態更新需要2nl+l次flops.

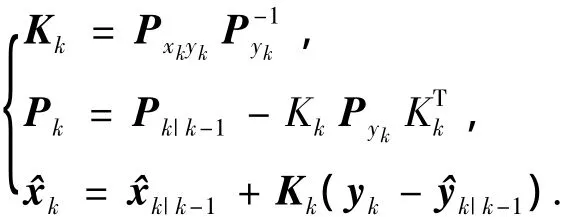
總結以上分析，CKF的復雜度fCKF總計為

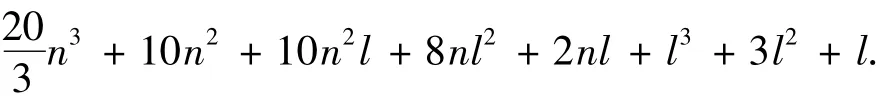
同理，可對UKF和CDKF進行分析，濾波參數的具體分析結果如表1所示.由表中數據可計算得到UKF的復雜度fUKF總計為

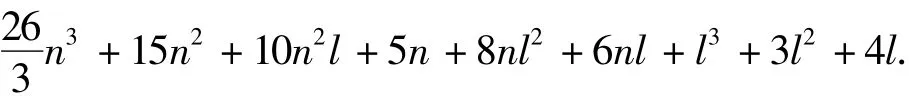
CDKF的復雜度fCDKF總計為

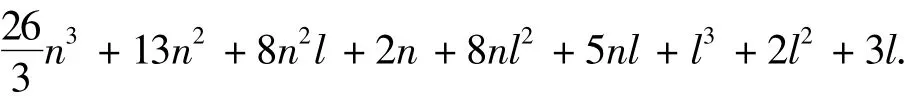
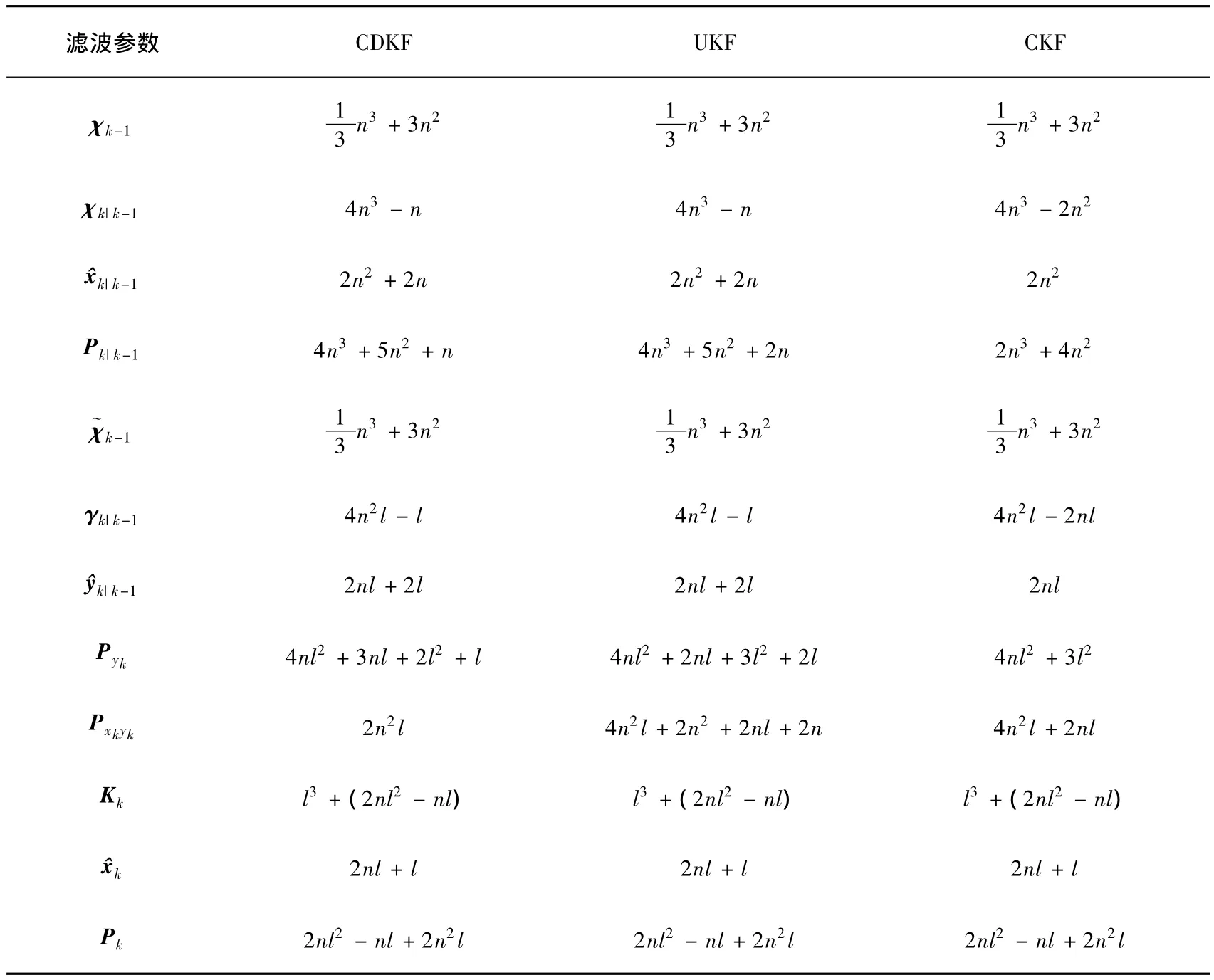
表1 確定性采樣卡爾曼濾波復雜度分析結果

由3個表達式可看出，CDKF、UKF、CKF 3種算法的復雜度均為O(n3)和O(l3)量級，即與狀態維數和量測維數均呈三次方關系.

通過對3種算法總體復雜度系數項的直觀比較可知:fUKF＞fCDKF和fUKF＞fCKF恒成立，即UKF的復雜度始終最高.而CDKF和CKF的復雜度難以通過系數項直接看出，所以將兩者求差得

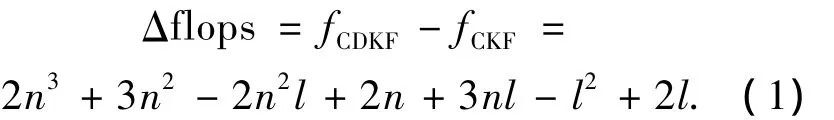
式(1)仍為狀態維數n的三次方形式，不便于分析.假設狀態維數n和量測維數l存在n-l=k的關系，其中k為整數，則式(1)可分別整理為關于n和l的二次項形式，即

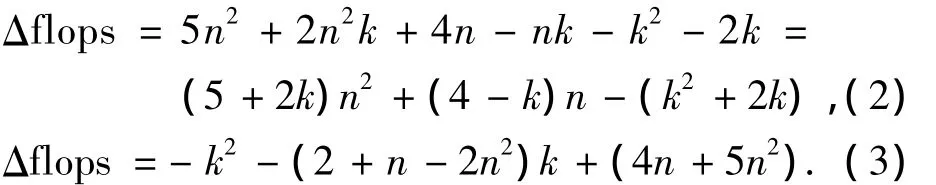
當0≤k＜n時，狀態維數大于量測維數，由式(2)可知Δflops為關于n的開口向上的拋物線，且n=1時Δflops＞0，所以Δflops為狀態維數n的單增函數，即狀態維數大于量測維數時，fCDKF＞fCKF恒成立，且隨著狀態維數增大，CDKF與CKF的差異也增大.

當k≤0時，量測維數大于狀態維數，由式(3)知Δflops為關于k的開口向下的拋物線，所以隨著k的不斷減小，會出現Δflops＜0的情況，即量測維數與狀態維數差異的不斷加大，CKF的復雜度會高于CDKF，即fCKF＞fCDKF.具體差異可根據實際系統的維數及前面的復雜度計算式進行計算得出.

為更為直觀的揭示三者之間的差異，根據復雜度計算式繪出了圖1、2所示的狀態和量測維數分別變化時3種算法復雜度的變化曲線.

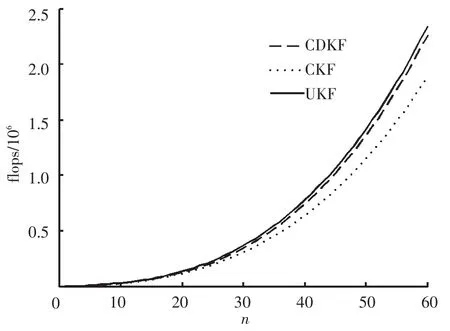
圖1 確定性采樣卡爾曼濾波復雜度(l=10)

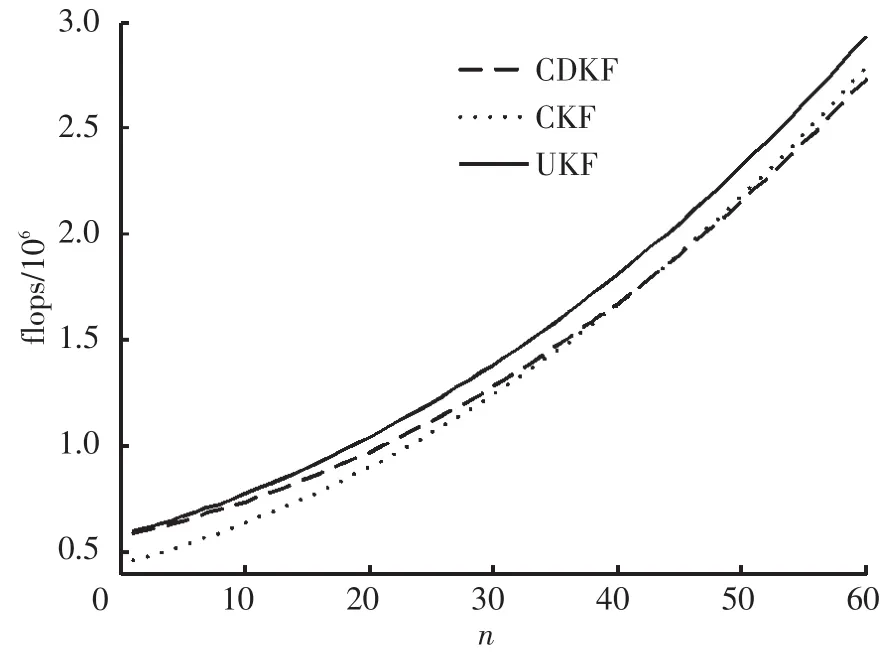
圖2 確定性采樣卡爾曼濾波復雜度(n=40)

2 仿真實驗與分析

為驗證UKF、CDKF和CKF算法復雜度分析的正確性及在精度上的一致性，分別將其應用于SINS/GPS的緊耦合導航中.

狀態方程選取大方位失準歐拉角非線性模型，具體見文獻［9］，狀態量為:x=［δψ，δθ，δγ，δVE，δVN，δVU，δL，δλ，δh，εx，εy，εz，▽x，▽y，▽z，bt，dt］T.其中，(δψ，δθ，δγ)為姿態誤差，(δVE，δVN，δVU)為速度誤差，(δL，δλ，δh)為位置誤差，ε和▽分別為陀螺和加速度計常值漂移，bt和dt分別為時鐘偏置和漂移.

利用4顆衛星的偽距與偽距率作為觀測量，則衛星i的量測值為yi，k=［ρi，k，ρi，k］，ρi，k為偽距，ρi，k為偽距率.具體非線性量測方程參見文獻［10］.

綜上可知，狀態維數為n=17，量測維數為l=8.根據前面對復雜度的分析，l=8時有fUKF＞fCDKF＞fCKF.

仿真中載體分別經過靜止、加速、爬升等階段.初始位置為(126.67°，45.78°，100 m).初始失準角為(5°，5°，20°).SINS傳感器各參數為:陀螺常值漂移100°/h，隨機漂移0.3°/;加速度計零偏0.001g(g=9.780 3 m/s2)，隨機噪聲偽距率量測噪聲為0.1 m/s;偽距量測噪聲為10 m;時鐘偏差為100 m;時鐘漂移噪聲為0.1 m/s.

隨機產生20組數據進行蒙特卡羅仿真.圖3、4分別給出了緊耦合的姿態和位置估計誤差曲線(20次仿真平均值).表2給出了確定性采樣濾波在SINS/GPS緊耦合導航中的估計精度(20組均方跟誤差的平均值).由圖3、4可知，基于確定性采樣原理的UKF、CDKF、CKF 3種算法均可使姿態和位置快速收斂，并且精度相近，只有可忽略的輕微不同.UKF、CDKF、CKF 3種算法的單次導航迭代耗時(20次仿真平均值)分別為7.23、6.92、6.74 ms.可見，UKF的復雜度最高，CDKF次之，CKF最低，與理論分析結果一致.

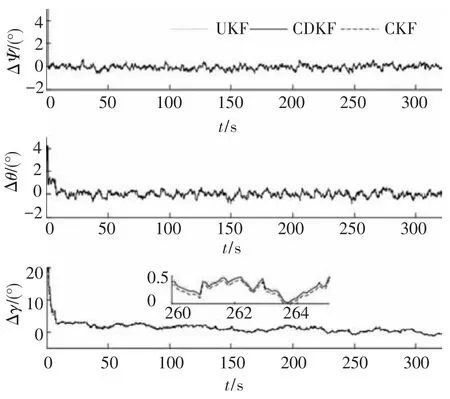
圖3 載體姿態誤差

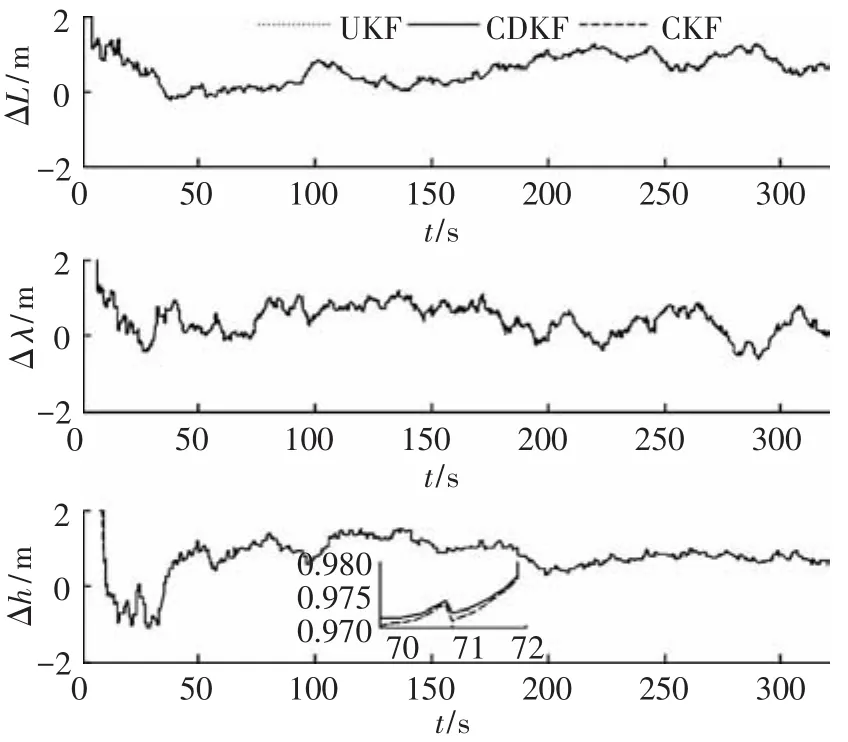
圖4 載體位置誤差

表2 SINS/GPS緊耦合導航估計性能

3 結論

1)針對確定性采樣非線性濾波的實時性問題，對UKF、CDKF和CKF 3種常用算法進行了復雜度分析，導出了復雜度計算的表達式.

2)通過進一步的差異性比較，表明3種算法中UKF復雜度最高;當狀態維數高于量測維數時，CDKF的復雜度低于UKF的復雜度，CKF的復雜度最低;量測維數相對狀態維數較高時，CDKF的復雜度會低于CKF的復雜度，在諸如雷達測距［11］等高維量測系統中選取CDKF可獲得最小的硬件開銷.

3)將3種算法應用于SINS/GPS的緊耦合導航中，仿真結果表明了分析結果的正確性.

［1］GREWAL M S，ANDREW A P.Kalman filtering，theory and practice using Matlab［M］.2nd ed.New York:John Wiley＆Sons，2008:225-289.

［2］姬曉琴，高曉穎.低軌衛星緊組合導航UKF方法［J］.哈爾濱工業大學學報，2012:44(7):135-138.

［3］王小旭，潘泉，黃鶴，等.非線性系統確定采樣型濾波算法綜述［J］.控制與決策，2012，27(6):801-812.

［4］MERWE R V D.Sigma-point Kalman filter for probabilistic inference in dynamic state-space models［D］.Portland:Oregon Health＆Science University，2004:108-110.

［5］ARASARATNAM I，HAYKIN S.Cubature Kalman filters［J］.IEEE Transactions on Automatic Control，2009，54(6):1254-1269.

［6］趙恒，蘇永清，葉萍.快速傳遞對準濾波器設計及其計算復雜度分析［J］.彈箭與制導學報，2011，31(3):31-34.

［7］HOLMES S A，KLEIN G，MURRAY D W.An O(N2)square root unscented Kalman filter for visual simultaneous localization and mapping［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31(7):1251-1263.

［8］KARLSSONR，SCHONT，GUSTAFSSONF.Complexity analysis of the marginalized particle filter［J］.IEEE Transactions on Signal Processing，2005，53(11):4408-4411.

［9］ALI J，MIRZA M.Performance comparison among some nonlinear filters for a low cost SINS/GPS integrated solution［J］.Nonlinear Dynamics，2010，61(3):491-502.

［10］LI Y，RIZOS C，WANG J，et al.Sigma-point Kalman filtering for tightly coupled GPS/INS integration［J］.Journal of the Institute of Navigation，2008，55(3):167-177.

［11］MCMANUS C，BARFOOT T.A serial approach to handling high-dimensional measurements in the sigmapoint Kalman filter［C］//Proceedings of Robotics Science and Systems.Los Angeles，CA:MIT Press，2011.