基于UIO的減搖鰭控制系統故障診斷算法

孫 蓉，劉 勝，李 冰

(哈爾濱工程大學自動化學院，150001哈爾濱)

為達到船舶安全航行以及穩定船舶航行姿態，目前廣泛采用減搖鰭裝置，這種主動減搖裝置集合了電子、機械以及液壓技術，通過測量船舶搖擺姿態信息，經控制器處理，輸出鰭角控制指令，經液壓驅動系統使鰭轉動，隨著變化的船舶橫搖運動而不斷地改變鰭運轉方向，產生抵抗海浪干擾的穩定力矩，從而達到穩定船舶的橫搖姿態的目的.

減搖鰭設備物理結構復雜，涉及技術較多，國內外進行了廣泛研究［1-5］.其減搖效果與采用的控制策略密切相關，目前廣泛采用變參數最優控制［6-7］、自適應控制［8-9］、模糊控制［10-11］、滑模變結構控制［12-14］等.由于減搖鰭工況環境以及自身設備儀器老化等原因，使減搖鰭控制系統產生故障，導致系統控制減搖鰭失效，危及船舶的安全航行．近幾年來，我國的船舶行業高速發展，對減搖鰭的減搖性能以及可靠性方面要求顯著提高．由于減搖鰭系統的先進性和結構的復雜性也使系統故障率大大提高，而且故障修復的時間也越來越長，這大大提高了減搖鰭控制系統故障的維修難度．本文以NJ5型減搖鰭控制系統為研究對象，采用基于模型的故障診斷方法，提出了一種UIO最優故障診斷算法，給出算法實現流程，算法采用離散迭代形式便于計算機實現，推導了NJ5型減搖鰭控制系統存在UIO最優故障診斷觀測器的充要條件，算法結構緊湊可靠適合工程實現．

1 問題描述

減搖鰭控制系統是一個典型的電液控制系統，為達到減搖鰭可靠運行的目的，本文設計了減搖鰭控制系統實時故障診斷算法，采用哈爾濱工程大學研制的NJ5型減搖鰭為原型，其中NJ5型減搖鰭控制系統原理圖如圖1所示．

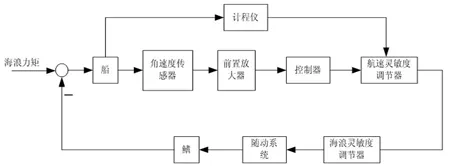
圖1 NJ5型減搖鰭控制系統原理圖

基于模型的減搖鰭控制系統故障診斷中，評價殘差信息判斷故障是否發生，對于隨動系統狀態空間描述為

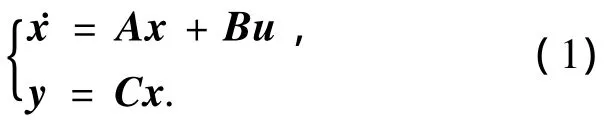
其中:x系統狀態，x=［a，a］T，a為鰭角，a為鰭角速度;y為鰭角輸出;u為隨動系統的鰭角指令，即為NJ5型減搖鰭航速靈敏度調節器的輸出電壓．

NJ5型減搖鰭的系統參數為

減搖鰭控制系統實質上是一個海浪隨機擾動下的船舶控制系統，集合了電子、電氣及液壓技術的復雜控制系統，統計了NJ5型減搖鰭使用情況，總結了該型減搖鰭的易發故障部位，本文結合NJ5型減搖鰭實際情況，考慮了控制系統的傳感器故障，為了便于系統實際應用實現，將式(1)進行離散化處理，則帶有傳感器故障以及模型不確定性Edk的隨動系統離散化模型為

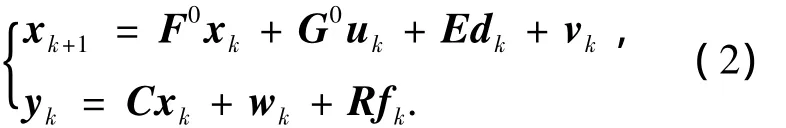
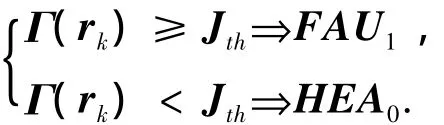
二元假設HEA0、FAU1分別為無故障狀態及故障狀態，本文目的為設計合適的殘差信號rk，Γ(rk)為待設計的殘差信號rk的函數.滿足邏輯關系為

2 減搖鰭控制系統的UIO觀測器設計

本節針對減搖鰭控制系統進行了最優濾波與魯棒故障診斷的研究，本節設計的全階UIO(未知輸入觀測器)，結構簡單，相比其他降階方法，其存在性更容易證明，在滿足干擾解耦的條件下還有更多的設計余度．本節給出了UIO的設計步驟并證明了其存在條件，利用干擾解耦原理，獲得了最優輸出估計．

為了估計式(2)描述的具有未知干擾及故障的減搖鰭控制系統狀態，提出了基于待設計參數為Fk+1、Tk+1、Hk+1、Kk+1的UIO最優故障診斷觀測器為

這種UIO最優故障診斷觀測器的結構框圖如圖2所示，將UIO最優故障診斷觀測器應用到減搖鰭控制系統，考慮帶有傳感器故障以及模型不確定性Edk的減搖鰭控制隨動系統式(2)以及UIO最優觀測器式(3)，可得到系統狀態估計誤差為

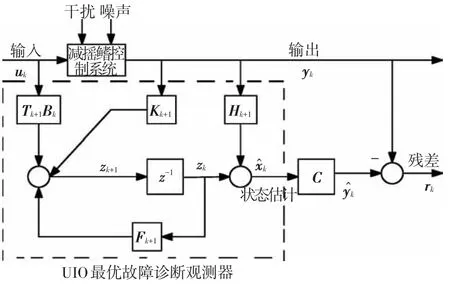
圖2 UIO最優故障診斷觀測器結構框圖

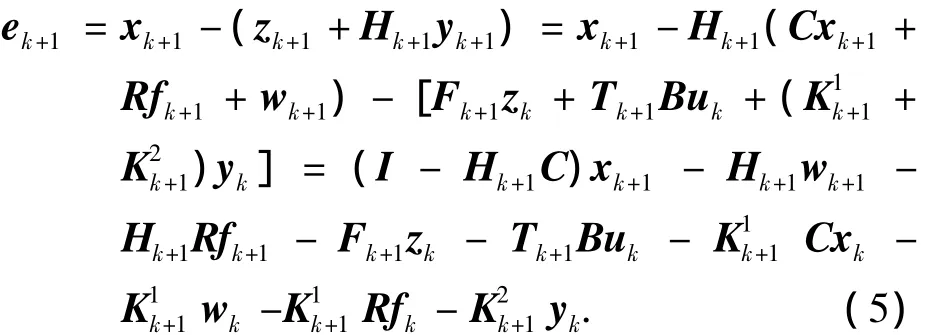
由UIO最優觀測器式(3)可知:zk=k-Hkyk，代入狀態估計k，因此有

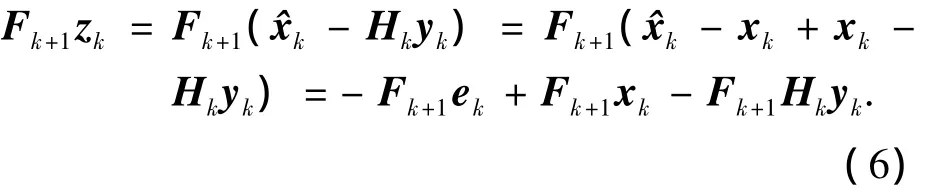
將式(6)代入狀態估計誤差ek+1，有

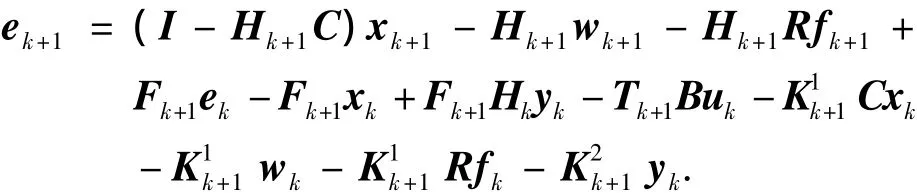
代入減搖鰭隨動控制系統離散化模型式(2)，有

本文設計的UIO最優故障診斷觀測器的目的是在減搖鰭控制系統的故障診斷過程中，減小誤報、漏報率，提高故障診斷的魯棒性，為達到設計目的，狀態估計誤差式(7)利用干擾解耦原理，因此設計的減搖鰭控制系統UIO最優故障診斷觀測器參數滿足方程

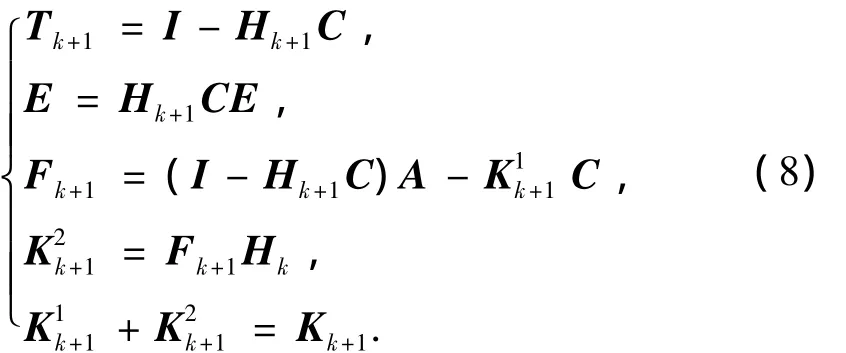
所以得到的干擾解耦的狀態估計誤差為

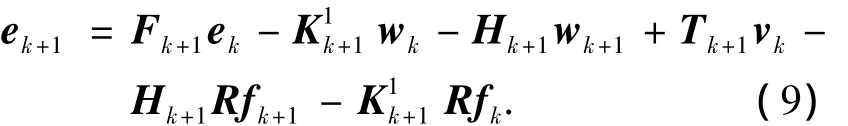
由式(9)可知，若Fk+1具有全部穩定的特征值，在無故障的情況下，狀態估計誤差ek+1漸進趨于零，即所設計的減搖鰭控制系統UIO最優故障診斷觀測器就是求解式(8)，并且Fk+1的特征值穩定.因此具有結構(3)的觀測器為減搖鰭控制系統(2)的UIO最優故障診斷觀測器的充要條件時，減搖鰭控制系統的狀態矩陣滿足如下定理．

定理1結構(3)為系統(2)的UIO最優故障診斷觀測器的充要條件為:1)rankCE=rankE;2)(C，A1)可觀測，其中A1=A-E［(CE)TCE］-1(CE)TCA.

證明充分性．當條件1)成立時，不失一般性，E假定為列滿秩矩陣，因此矩陣CE為一列滿秩矩陣，所以CE存在左逆陣(CE)+=［(CE)TCE］-1(CE)T，則由E=Hk+1CE，得Hk+1的特解為

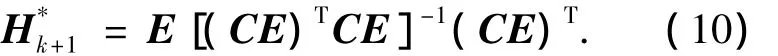
則UIO最優故障診斷觀測器的系統動態陣為

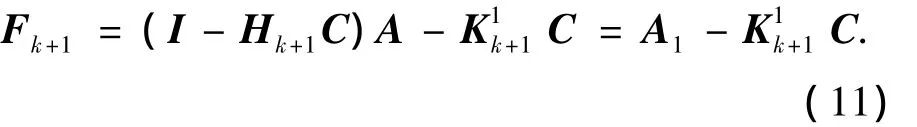
由式(11)可知，通過合理地設計故障診斷觀測器參數K1

k+1可使系統陣Fk+1穩定，滿足UIO故障診斷觀測器可干擾解耦的參數由式(8)可解．因此設計的結構(3)故障診斷觀測器為減搖鰭控制系統的UIO最優故障診斷觀測器．

證明必要性．因為結構(3)為系統(2)的UIO最優故障診斷觀測器，且未知擾動分布陣E為列滿秩矩陣，因此矩陣Hk+1的通解可求，即

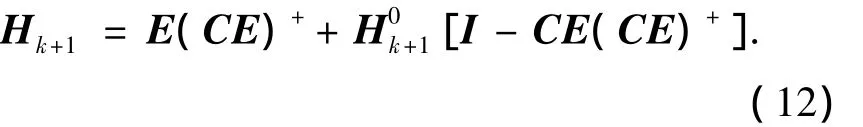
其中:H0k+1為任意陣，(CE)+為CE的左逆，即

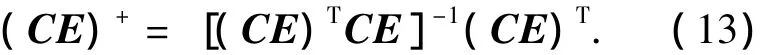
將式(12)代入UIO最優故障診斷觀測器的系統動態陣Fk+1，得

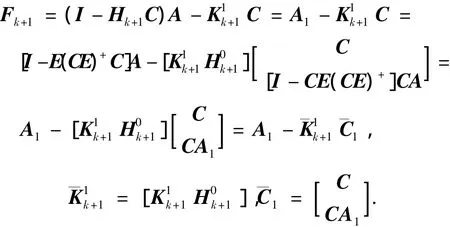
由于系統狀態陣Fk+1穩定，則矩陣對(，A1)可觀測，因此矩陣對(C，A1)可觀測.

針對數學易錯題、典型習題，通過微課程的整合，分門別類整理，或者講解易錯的地方，強調錯誤點，方便學生進行糾錯，或者從問題引導學生思考，為學生創造一個最近發展區，構建一類問題解決的策略.對于自己解決不了的問題，可以通過先看具體的解答步驟，或多次重復觀看，依據微視頻的幫助，掌握解題技能，形成策略性知識，發展數學思維，培養學習興趣.

結構(3)為減搖鰭控制系統(2)的UIO最優故障診斷觀測器的充要條件1)說明了可解耦的最大干擾的個數不能大于獨立測量的數目，當系統無未知擾動時，由式(8)可知，UIO最優故障診斷觀測器退化為全階Luenberger觀測器，這也解釋了為什么Luenberger觀測器存在的條件只要滿足(C，A)可觀測，通過比較分析也能看出本節提出了UIO故障診斷觀測器對系統的故障診斷更具一般性，當系統存在未知擾動時，可有效地減小干擾對診斷效果的影響，達到魯棒故障診斷的目的，減小誤報、漏報率，對實際系統的應用更具現實意義．

當減搖鰭控制系統滿足UIO最優故障診斷觀測器設計條件時，設計的故障診斷觀測器的狀態估計誤差方差決定了設計觀測器的質量．

狀態估計方差陣為

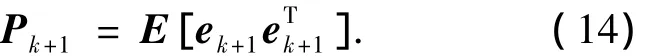
代入狀態估計誤差式(9)，則

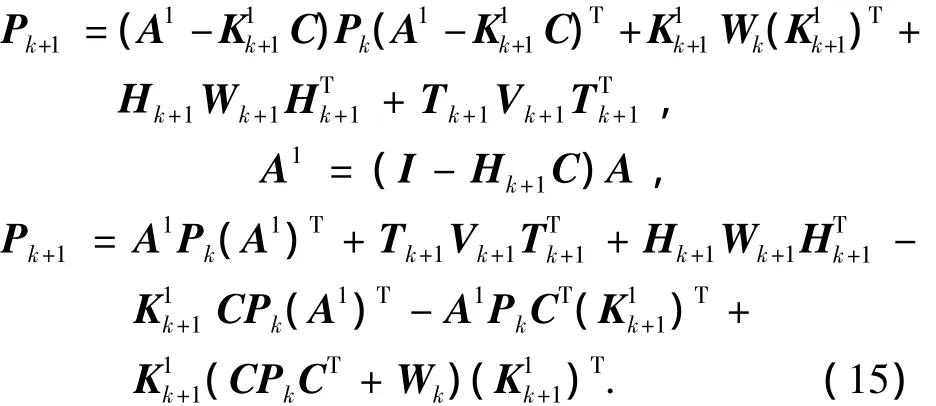
因為CPkCT+Wk為正定陣，所以存在矩陣ζ，滿足

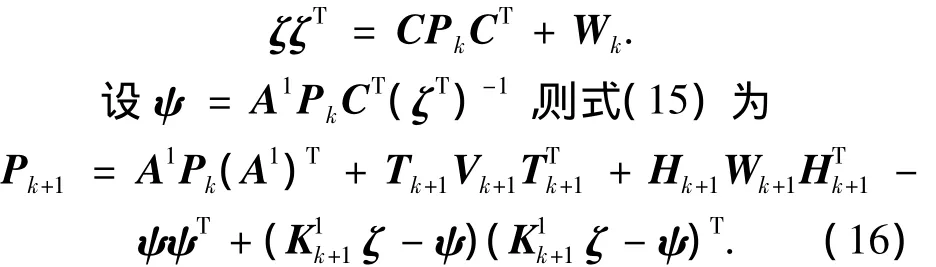
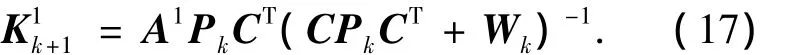
基于上述推導，本節給出了減搖鰭控制系統UIO最優故障診斷觀測器設計實現流程:1)設置初值P0，由式(3)可知z0=x0-CE(CE)+y0，H0=0，K=0.2)由式(10)計算Hk+1.3)由式(17)計算K1k+1.4)通過解式(8)，計算Tk+1，Fk+1，5)由UIO最優故障診斷觀測器結構(3)，計算狀態估計k+1及zk+1.6)通過狀態估計方差陣式(16)計算狀態估計方差Pk+1.7)設置k=k+1，繼續下一步計算.

3 故障決策算法設計

殘差信號是在故障診斷決策中用來表征故障的待設計信號，因此殘差信號設計質量決定了故障診斷的水平，基于模型的故障診斷的核心問題即為殘差的設計，結合NJ5型減搖鰭控制系統，考慮實際應用環境以及對船舶航行安全性重要影響，本節利用統計決策規則給出了一種門限閾值設計方法．

構造殘差信號為

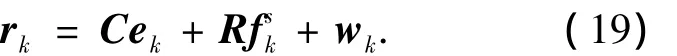
當系統為無故障狀態H0時，由式(19)可知

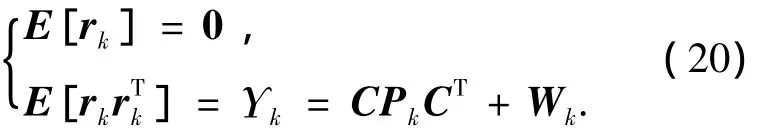
由式(20)可見，當系統為FAU1時，殘差的統計特性與HEA0不同，故障檢測的目的就是構建一個決策函數，當決策函數超出預設閾值時，判定系統為FAU1.構造如下故障檢測決策函數為

由式(20)的殘差統計特性可知，故障檢測決策函數服從χ2分布，故障檢測邏輯關系為

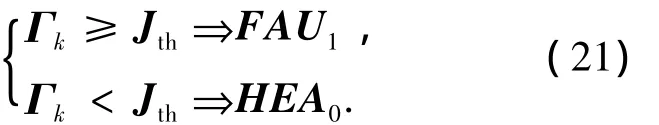
其中:Jth為故障檢測門限閾值，由χ2分布表確定.

當給定系統故障檢測誤報率指標Pf時，則通過查找χ2分布表，式P［Γk≥Jth｜HEA0］=Pf中故障診斷門限閾值Jth可求.比較邏輯關系式(21)，可判斷故障是否發生.

4 仿真驗證

為了驗證本文提出的UIO最優故障診斷觀測器診斷方法(定義為方法1)的效果，以及相比于未考慮干擾解耦診斷方法(定義為方法2)的優越性，本文以NJ5型減搖鰭控制系統為研究對象，在Matlab仿真環境下驗證了算法的有效性．

NJ5型減搖鰭控制系統的連續模型如式(1)所示，系統參數為

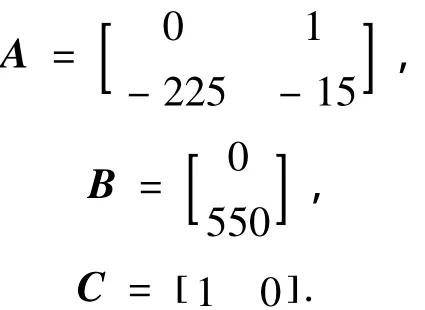
為了方便實際應用實現，采用離散形式的系統模型，如式(2)所示，由F0=eAT，G0=，可知離散形式的系統參數.設系統未知擾動分布陣Wk=0.12I3×3，uk=8，x0=0，故障為

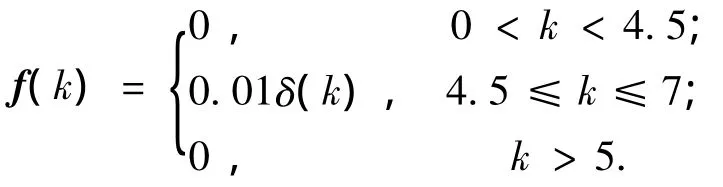
圖3～8給出了提出的UIO最優故障診斷觀測器的鰭角、鰭角變化率的估計、殘差以及傳統算法的殘差．由圖3、4可以看出，在本文的UIO最優故障診斷觀測器估計下，得到的鰭角估計誤差的絕對值要小于未考慮未知擾動的方法2，在收斂速度上，本文提出的UIO最優故障診斷觀測器在15 s左右收斂，而對比于傳統的未考慮干擾解耦的故障診斷算法的收斂性差的缺陷，本文提出的算法減小了故障診斷時間，提高了故障診斷效率．圖4表征了方法2以及本文算法鰭角變化率估計誤差的特性，結果表明，本文算法的收斂性優于方法2，在估計精度上，本文算法提高了鰭角變化率的估計精度．圖5描述了系統殘差情況，圖6為其局部放大圖，從圖5、6可知，系統殘差達到了對未知擾動解耦的目的，解耦后的殘差為小量且收斂到零，圖7為在假設故障情況下的殘差，當給定故障診斷系統性能指標，設定合理門限可實時診斷出故障，為后續容錯控制提供保證，對比方法2的殘差(見圖8)，顯而易見，本文算法構造的殘差收斂性更好，可以有效地減小故障診斷的誤報率．

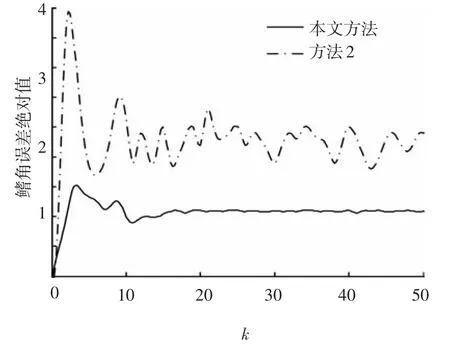
圖3 鰭角估計誤差絕對值

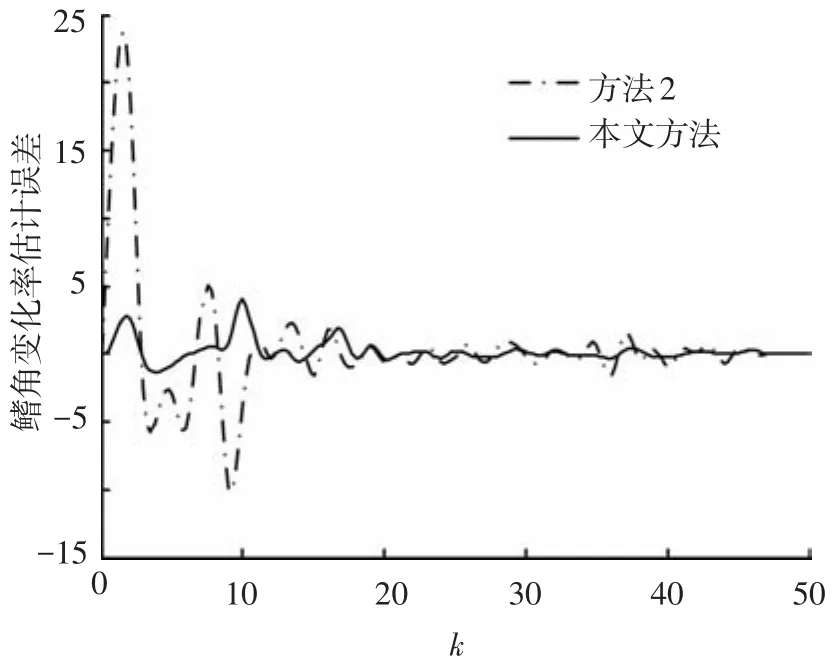
圖4 鰭角變化率估計誤差

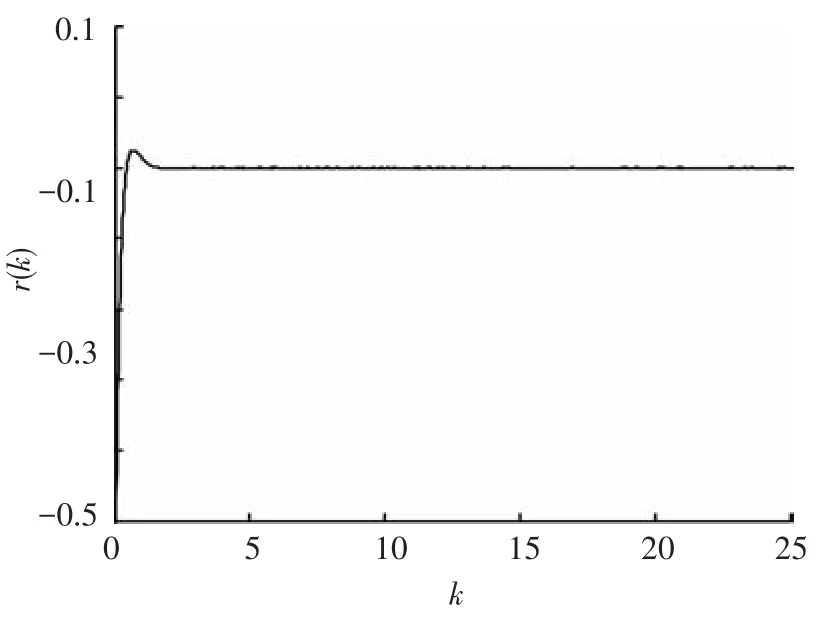
圖5 本文算法殘差

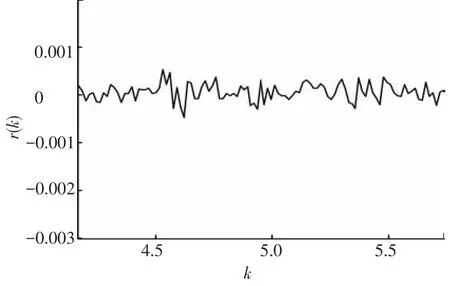
圖6 本文算法殘差局部放大圖

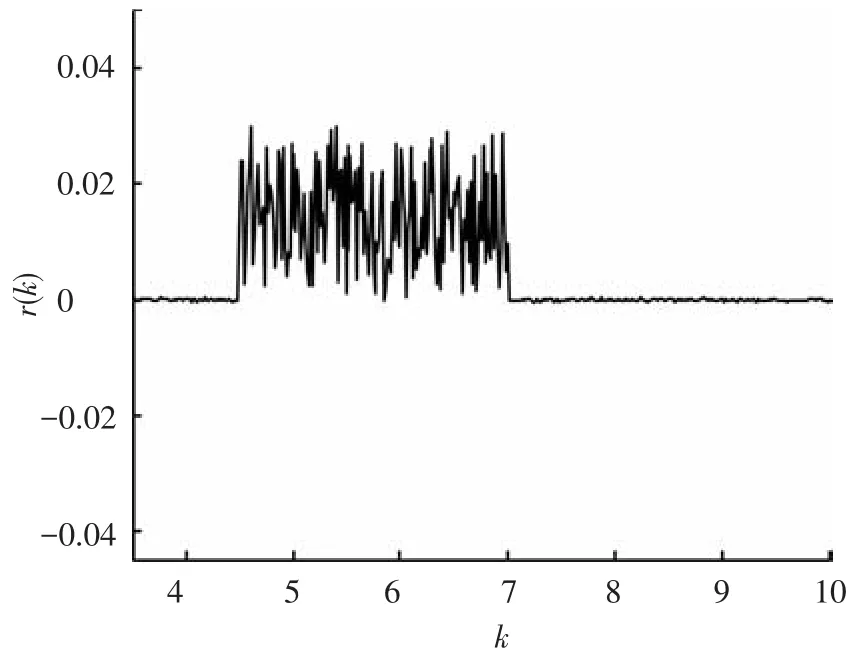
圖7 系統故障狀態下的殘差

圖8 方法2殘差

5 結論

1)針對減搖鰭控制系統設計了一種UIO最優故障診斷觀測器，設計的UIO最優故障診斷觀測器相比未考慮未知擾動的診斷方法，得到的狀態估計誤差小.

2)狀態估計誤差的收斂性比較，UIO最優故障診斷方法要優于未考慮干擾解耦診斷方法，達到了快速收斂.

3)故障診斷階段，UIO最優故障診斷方法的殘差收斂效果要優于未考慮干擾解耦診斷方法，提出的UIO最優故障診斷方法快速響應了系統出現的故障.

4)減搖鰭控制系統是船舶安全航行的重要保證，提出的算法易于計算機實現，算法結構可靠，適合工程實現.

［1］金鴻章，王帆.零航速仿生減搖鰭水動力模型改進［J］.機械工程學報，2010，46(23):89-92.

［2］金鴻章，高妍南，潘立鑫，等.基于改進積分型變結構控制器的近水面機器人減搖鰭系統［J］.控制與決策，2011，26(4):57-64.

［3］PEREZ T，GOODWIN G C.Constrained predictive control of ship fin stabilizers to prevent dynamic stall［J］.Control Engineering Practice，2008，16(4):482-494.

［4］LEE S K，RHEE K P，CHOI J W.Design of the roll stabilization controller，using fin stabilizers and pod propellers［J］.Applied Ocean Research，2011，33(4):229-239.

［5］WANG Fan，JIN Hongzhang，QI Zhigang.Modeling for active fin stabilizers at zero speed［J］.Ocean Engineering，2009，36(17/18):1425-1437.

［6］SAGER S.Reformulations and algorithms for the optimization of switching decisions in nonlinear optimal control［J］.Journal of Process Control，2009，19(8):1238-1247.

［7］LOGIST F，SAGER S，KIRCHES C，et al．Efficient multiple objective optimal control of dynamic systems with integer controls［J］.Journal of Process Control，2010，20(7):810-822.

［8］NHAN T N.Optimal control modification for robust adaptive control with large adaptive gain［J］.Systems＆Control Letters，2012，61(4):485-494.

［9］DANIEL E M.A new approach to adaptive control:no nonlinearities［J］.Systems＆Control Letters，2003，49(1):67-79.

［10］QI Ruiyun，MIETEK A B.Stable indirect adaptive control based on discrete-time T-S fuzzy model［J］.Systems＆Control Letters，2003，49(1):67-79.

［11］BOULKROUNE A，TADJINE M，M’SAAD M，et al．Fuzzy adaptive controller for MIMO nonlinear systems with known and unknown control direction［J］.Fuzzy Sets and Systems，2010，161(6):797-820.

［12］DALY J M，WANG D W L.Output feedback sliding mode control in the presence of unknown disturbances［J］.Systems＆Control Letters，2009，58(3):188-193.

［13］GOUAISBAUT F，DAMBRINE M，RICHARD J P.Robust control of delay systems:a sliding mode control design via LMI［J］.Systems＆Control Letters，2002，46(4):219-230.

［14］EDWARDS C，TAN C P.Sensor fault tolerant control using sliding mode observers［J］.Control Engineering Practice，2006，14(8):897-908.