基于切換多胞系統的高超聲速飛行器魯棒控制

吳振東，王 青，董朝陽，李 瑋

(1.北京航空航天大學自動化科學與電氣工程學院，100191北京;2.北京航空航天大學航空科學與工程學院，100191北京)

由于高超聲速飛行器的飛行包線跨度大，在工作包線內呈現出復雜的時變非線性特點，給其控制系統設計帶來很大的挑戰.針對飛行器的大包線控制問題，工程上常采用增益調度方法設計控制器［1］，設計過程簡單，簡化了控制器的設計與實現，在高超聲速飛行器X-43A的試飛過程中采用了此方法［2］.但是該設計方法控制器參數按開環方式改變，閉環控制系統的穩定性難以從理論上獲得保證.

為了彌補增益調度設計方法的不足，近年來學者將切換系統理論應用于高超聲速飛行器大包線飛行的控制器設計中［3-5］.文獻［3］設計了大包線自適應切換控制器，分析了閉環系統的穩定性，解決了高超聲速飛行器巡航段大包線飛行控制問題;文獻［4］給出了基于間隙度量的大包線切換LPV控制方法，設計了各子區域的LPV控制器，分析了閉環系統的穩定性.以上文獻均保證了大包線飛行控制系統的穩定性，且優化了控制器切換的過渡過程，一定程度實現平滑切換，卻難以從根本上消除控制切換帶來的輸出跳躍.Hou以切換多胞系統描述大包線飛行動態，給出了確保飛行包線范圍漸近穩定的控制器插值方法，從根本上克服了傳統切換控制的跳躍問題［5］.此外，現有的切換多胞系統大多依賴于公共Lyapunov函數方法實現對控制系統的分析與綜合［4-5］，要求多胞的每個頂點和整個多胞區域內都存在一個公共的Lyapunov矩陣函數，具有較大的保守性.本文針對上述問題，將高超聲速飛行器包線范圍內的飛行動態建模為切換多胞系統，采用基于參數依賴Lyapunov函數與平均駐留時間方法給出包線范圍漸近穩定的條件，設計了確保多胞系統在參數任意快變下穩定的反饋控制器，所得控制器能夠在保證系統穩定的前提下，克服切換控制器的輸出跳躍現象，并降低了系統分析與設計的保守性.

1 高超聲速飛行器切換多胞系統建模

以高超聲速飛行器［6］的縱向飛行動態為例，不失一般性，僅考慮飛行器的縱向短周期運動，假定每一個工作點處的縱向短周期線性模型可以表征工作點附近的飛行動態.設飛行包線內N個工作點所對應的動力學系統描述為

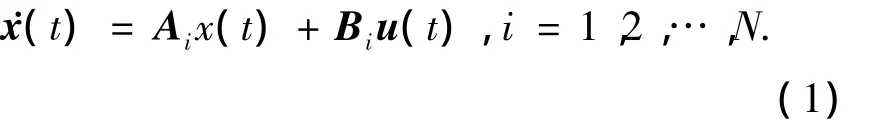
其中:x(t)=［αq］T為系統狀態，α，q分別為迎角和俯仰角速率，u(t)=[ξeη]T為控制輸入，ξe為升降舵偏轉角，η為節流閥調定指令，Ai、Bi分別為飛行包線內第i個工作點的系統矩陣和控制輸入矩陣，i為工作點標號.

采用切換多胞系統建立高超聲速飛行器包線內的飛行動力學模型過程是將整個包線內的工作點根據調度變量(如馬赫數和高度等)劃分為不同的組，每組對應包線內的一個區域，以每一區域建模為一個多胞系統，系統的頂點即為該區域內的工作點，頂點的動態特性由工作點處的線性小擾動方程表征，多胞系統內部的飛行動態通過頂點系統動態的線性加權獲得，則該區域內的飛行動力學特性由該多胞系統近似描述;然后將各飛行區域視為一個獨立的多胞子系統，將飛行軌跡在相鄰多胞子系統間的穿越視為子系統間的切換，則整個飛行包線內的飛行動力學可用一個切換多胞系統描述.其中，每個多胞子系統的工作點選取原則是使多胞系統的工作點狀態空間模型相差盡量小，這樣有利于性能品質的提高，因為若將多個模型相差較大的工作點劃分在同一區域，設計控制系統會因為魯棒性的要求而犧牲指標性能，常用的工作點選取方法可采用奇異值判定方法和間隙度量方法［4］.

需要注意的是，為保證得到的多胞子系統可完整地覆蓋整個飛行包線，相鄰的多胞子系統需要滿足局部重疊的特性［7］，即相鄰的多胞子系統需包含公共的工作點.

基于切換多胞系統建立飛行器包線內的飛行動力學模型過程可以圖1為例簡單說明.考慮高超聲速飛行器的再入高度變化從25 km到40 km，馬赫數變化從16到14，此包線飛行動態可以由18個工作點處的模型包絡，根據馬赫數的變化劃分成3組，得到3個飛行區域，建立相應3個多胞子系統;工作點5～8為多胞子系統1和2包含的公共工作點，工作點12～14為多胞子系統2和3包含的公共工作點，保證此3個多胞子系統可覆蓋整個飛行包線，且當飛行軌跡穿越相鄰多胞子系統間的邊界時，將其視作飛行動力學多胞系統模型的切換，則整個飛行包線的飛行動力學可采用切換多胞系統描述.

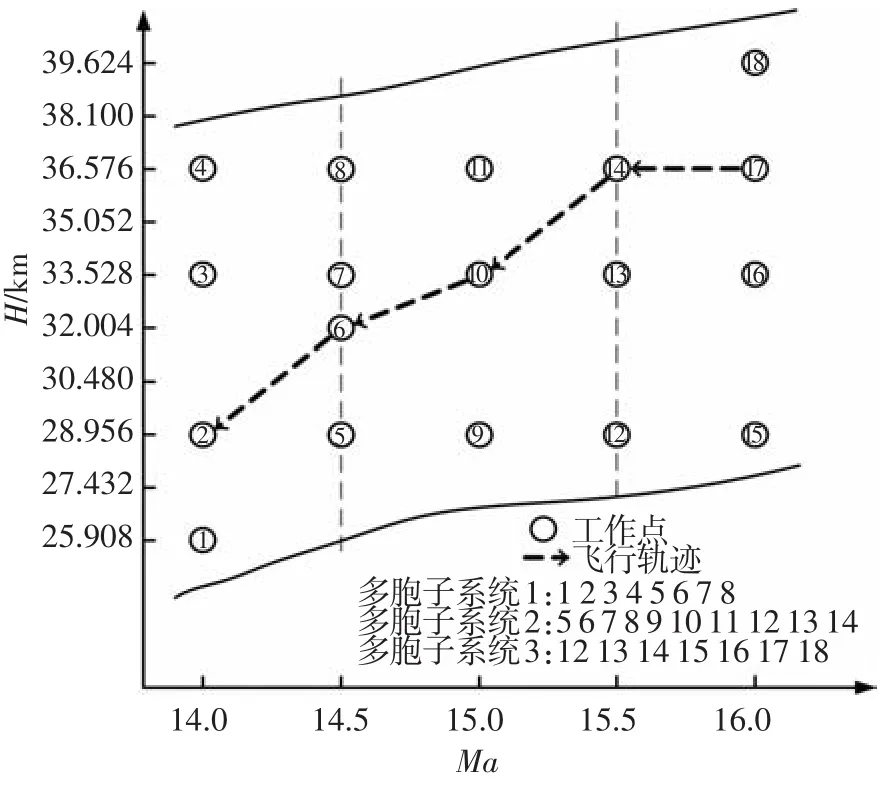
圖1 高超聲速飛行器的切換多胞系統建模示意圖

根據上述的切換多胞系統建模方法，將整個工作點模型集劃分為k個子集，相應地，工作點標號全集Ω被劃分為子集Ω1，Ω2，…，Ωk.飛行包線內的高超聲速飛行器的飛行動態采用不確定性切換多胞系統描述為

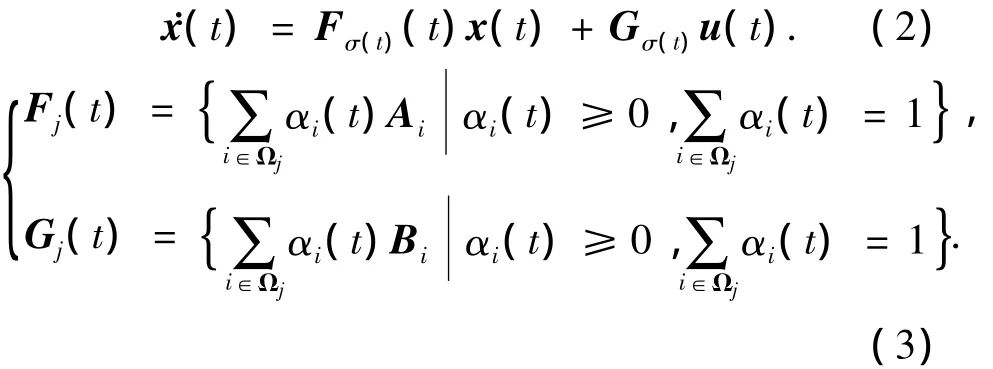
式中:σ(t)∈［0，+∞)→Ω={1，2，…，k}為切換律，表征飛行器工作區域隨時間變化規律;j∈S，S={1，2，…，k}為切換律的索引集;k為飛行包線內多胞子系統的個數;j為工作點所在工作區域的標號，子系統Ωj要滿足多胞系統模型對飛行器所有工作點完全覆蓋的條件Ωj=Ω，且要保證相鄰的多胞子系統間的公共子系統滿足=Ωj∩Ωj+1≠?.

由于鄰近的兩個多胞子系統公共邊界上的飛行動力學僅由多胞子系統公共設計點的飛行動力學得到，因此，切換多胞系統的切換不會引起系統矩陣參數不連續的變化，即對于整個飛行包線來說，Fσ(t)和Gσ(t)是連續變化的.

飛行器控制系統設計任務是實現控制系統的穩定和對給定指令信號的跟蹤控制，針對高超聲速飛行器的切換多胞系統(2)，設計控制器為

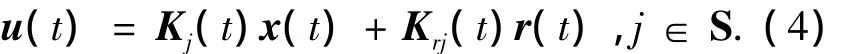
式中:Kj(t)、Kri(t)分別為控制器中的反饋控制律和前饋控制律，r(t)為給定的指令信號.

2 控制器設計和穩定性分析

定義1 對切換多胞系統(2)的切換信號σ(t)，令 ΔT＞0為公共子系統工作總時間，Nσ(ΔT)為ΔT內的切換次數.若存在N0≥0，τa＞0，使得成立，則稱 τa為平均駐留時間，下文中以 T［τa，N0］表示滿足平均駐留時間的切換律集合.

針對切換多胞系統(2)中的單個多胞子系統，給出如下穩定性引理.

引理1［8］多胞線性系統(2)的自治多胞子系統魯棒穩定的充分條件為存在正定矩陣Pi(i∈Ωj)及適維矩陣Yi滿足矩陣不等式

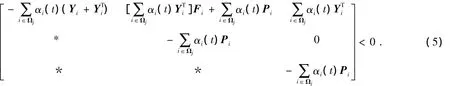
引理1通過引入松弛變量Yi，使得矩陣不等式中不再出現正定矩陣與系統矩陣的乘積項，降低了反饋控制綜合問題的求解難度［9］.式(5)矩陣不等式中的*表示矩陣中元素所在位置對稱塊的轉置，下文中與此表示的意義一致.

定理1 對于切換多胞系統(2)，若多胞子系統的頂點，存在矩陣Pi(i∈Ωj)，適維矩陣Ui及Vi滿足

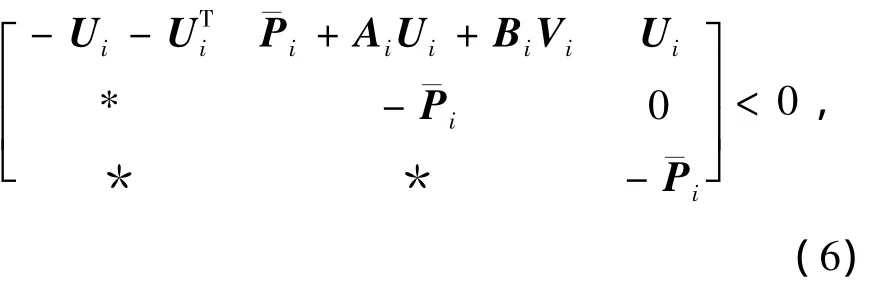
且切換多胞系統切換律σ(t)∈T［τa，N0］滿足平均駐留時間τa約束

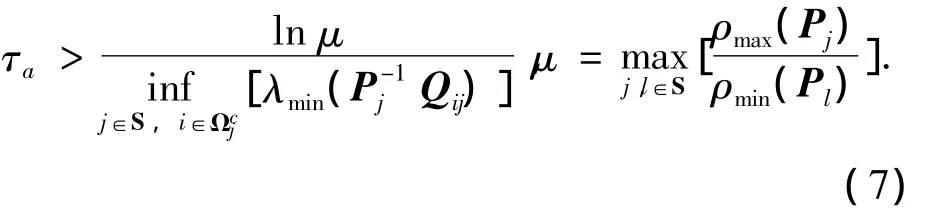
式中:ρmax(·)，ρmin(·)分別為矩陣的最大奇異值和最小奇異值，λmin(·)為最小特征根，Qij由公共子系統工作點求取.則控制器(4)中鎮定反饋控制器Kj(t)的參數選取為

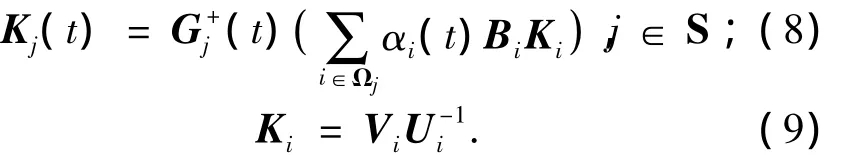
可保證對任意切換律σ'(t)∈T［τa，N0］，閉環切換多胞系統在零輸入情況下漸近穩定.其中，(t)是(t)的M-P偽逆.

證明 設存在正定矩陣(i∈Ωj)，適維矩陣Ui及Vi滿足線性矩陣不等式組(6)，下面首先證明式(9)給出的控制器增益矩陣使得切換多胞系統魯棒穩定.

由式Ui+UTi＞0，可知Ui可逆，則式(9)中矩陣Ki的存在性顯然.用diag{Ui-1，Ui-1，Ui-1}對式(6)進行全等變換可得

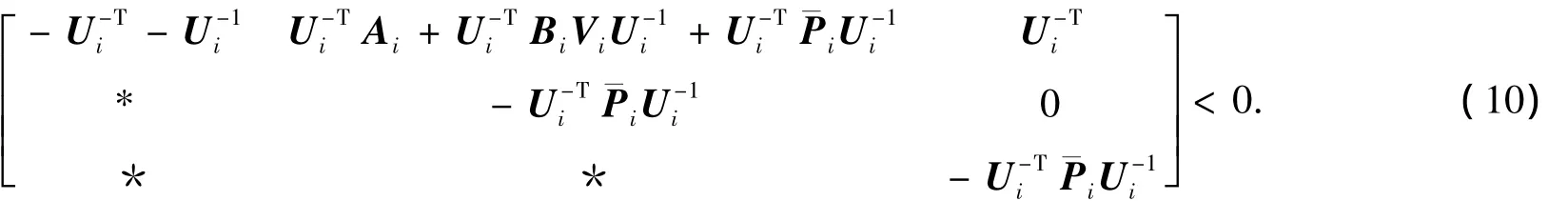
假設第p和q個多胞子系統間的公共子系統工作時長為t*，則有

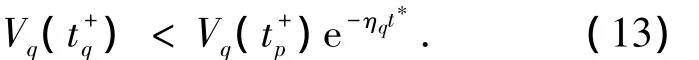
其中:

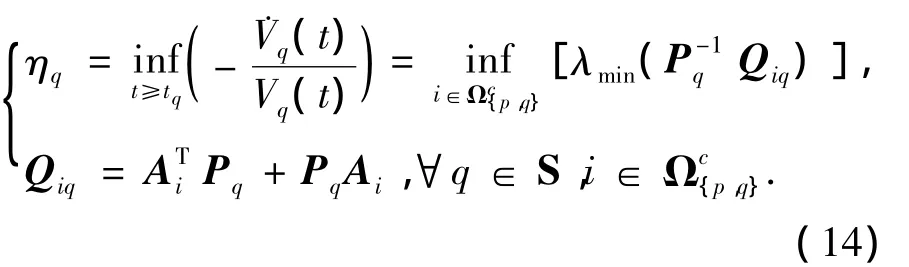
將式(14)代入式(13)，有

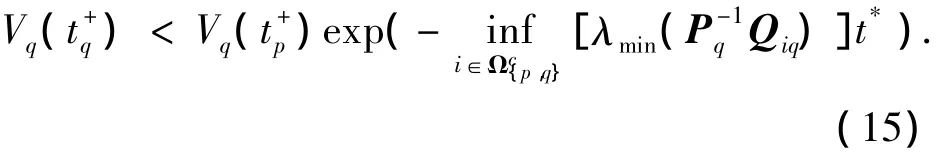
結合式(15)和式(16)，可得

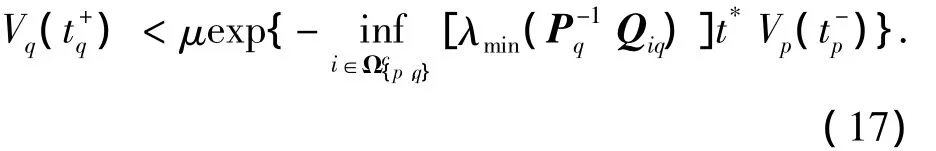
以t1，t2，…，tNσ(ΔT)分別表示各公共子系統相繼激活時刻，且各子系統工作時間分別為Δt1，Δt2，…，ΔtNσ(ΔT)，顯然，ΔT=Δt1+Δt2+…+ΔtNσ(ΔT).將多胞公共子系統從1到Nσ(ΔT)重復，如式(13)的推導方式，并結合式(17)，有

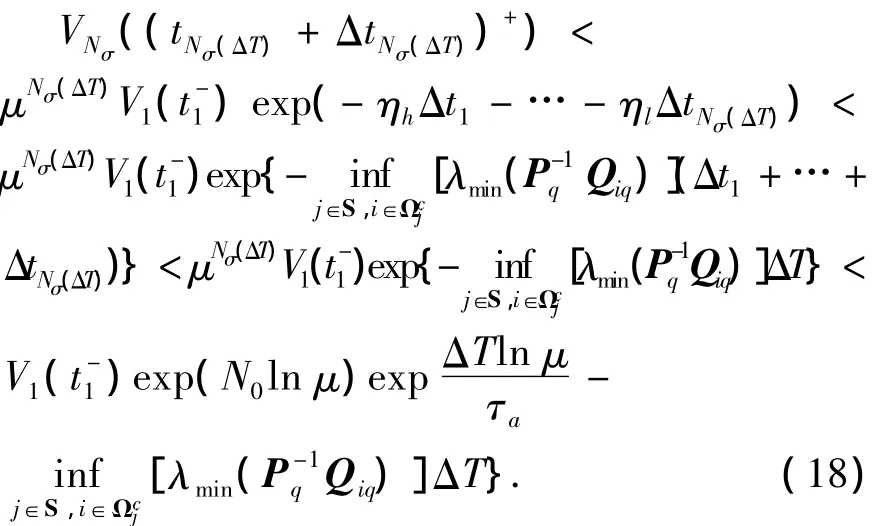
由式(7)可知

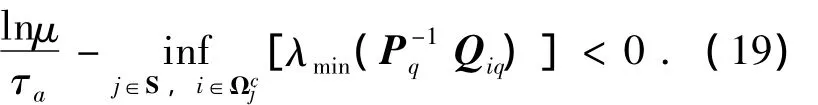
也即當ΔT→+∞時，必然存在ΔT*＞0使得下式成立.

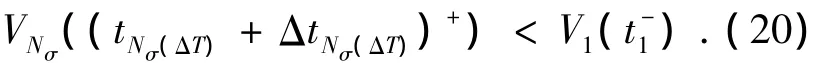
由上式可知多胞子系統之間切換時Lyapunov函數值單調遞減，同時，考慮到任意多胞系統在子切換律作用下Lyapunov函數值遞減，因此，切換多胞系統(2)在切換律σ(t)∈T［τa，N0］作用下全局漸近穩定.

文獻［5］中對P作了較為苛刻的限制，要求多胞子系統的每個頂點(即整個多胞系統)都存在一個共同的Lyapunov函數矩陣P，因而具有較大的保守性，而定理1要求對于切換多胞子系統的頂點i，可以存在不同的正定矩陣Pi滿足式(6)，即相對而言，定理1具備更低的保守性.

定理1中式(8)所示控制器Kj(t)的形式可視為對區域內邊界工作點的狀態反饋增益陣插值，需要實時獲得σ(t)和α(t).這在實際飛行中很容易實現，將所有工作點處的高度和馬赫數以數據表的形式裝訂至控制器，傳感器實時測量高度和馬赫數，控制器通過查表和插值方式獲得權值向量σ(t)和α(t)，由于飛行器動態在飛行區域內部及飛行區域間變化的連續性，即α(t)的連續性，保證了控制器插值的連續性，進而確保了控制器輸出不會發生跳變.

為了使系統的輸出y(t)跟蹤有界分段連續的參考指令信號r(t)，控制器(4)中前饋控制律Krj(t)參數選取為

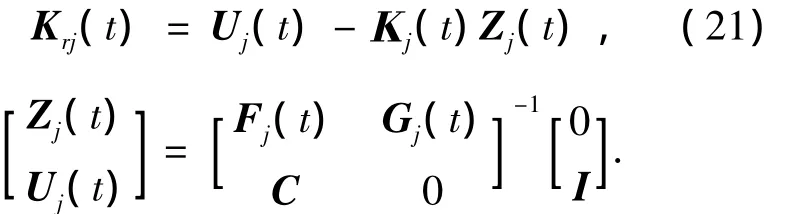
式中:C為系統輸出矩陣.在系統鎮定的情況下，按式(21)設計的前饋控制律Krj(t)可以實現對給定指令信號r(t)的無差跟蹤［10］.

3 仿真驗證

為驗證本文方法的有效性，采用文獻［6］的高超聲速飛行器模型，大包線內控制器的綜合以包線內18個工作點為基礎，如圖1所示，所選擇的工作點以馬赫數和高度為調度變量，各工作點的平衡條件見表1.

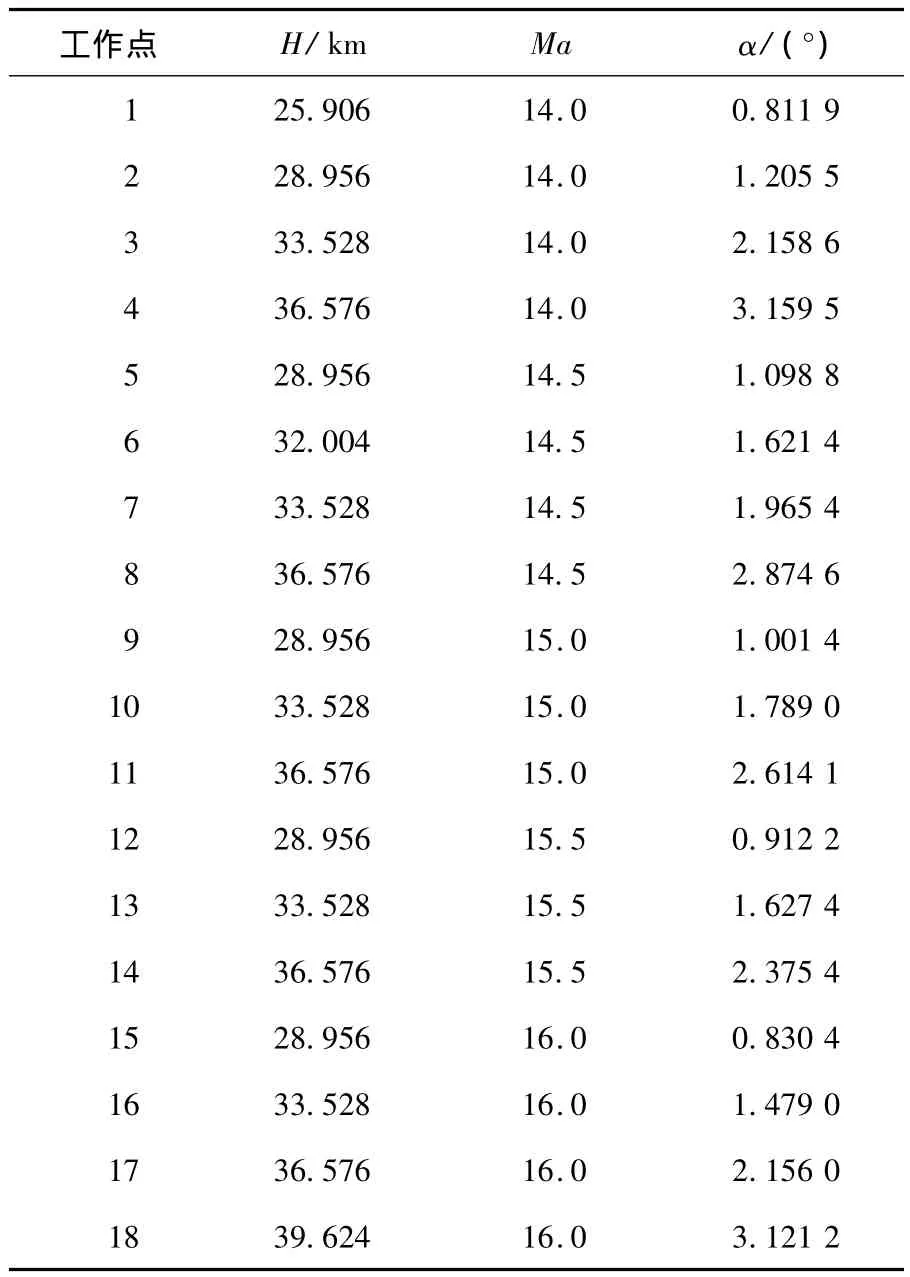
表1 高超聲速飛行器飛行包線范圍內的工作點

根據前述的切換多胞系統建模方法，飛行包線內所選擇的18個工作點可根據馬赫數分成3組，即建模為3個多胞子系統，各多胞子系統包含的工作點為

由定理1獲得切換多胞系統的各工作點控制器增益Ki如表2所示，對于每一個多胞子系統，子狀態反饋控制器Kj(t)采用式(8)進行插值，前饋控制律Krj(t)依據式(21)進行計算，給定C為單位陣.以包線內Ma∈［14.5，15)，H∈［29，36.5)的飛行區域說明狀態反饋控制器Kj(t)的插值過程:在此飛行區域內，子控制器的鎮定反饋控制增益通過設計點5、8、9和11上的4個反饋控制增益K5，K8，K9，K11進行插值得到，對于該飛行域內的某一特定的高度hx和馬赫數Max，插值得到的鎮定反饋控制增益K為

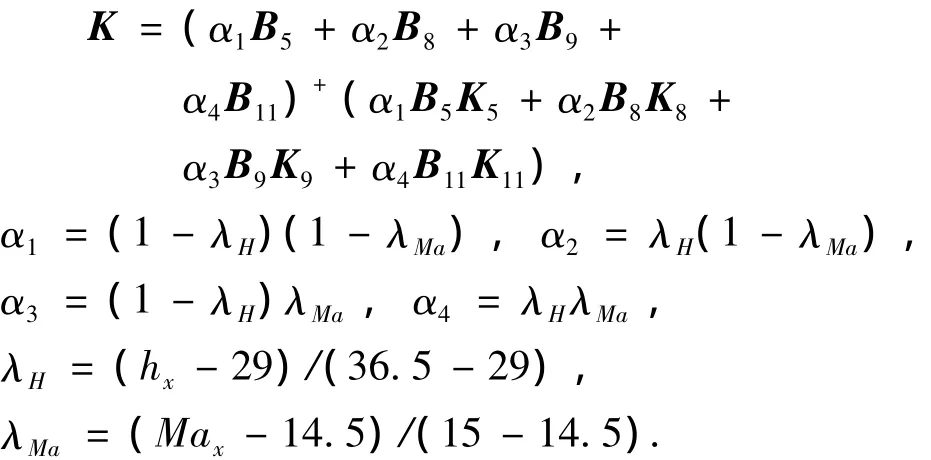
表2 工作點處的控制器增益

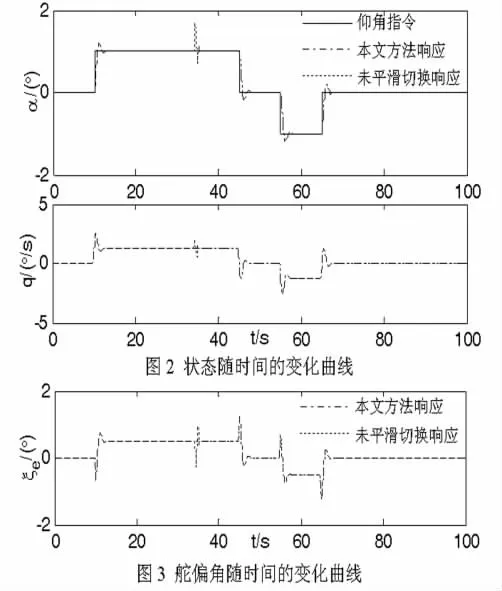
不失一般性，考慮高超聲速飛行器的工作點變化軌跡17—14—10—6—2，可見在工作點14、6處發生多胞切換，仿真結果如圖2、3所示.

由仿真結果可知，本文方法可以很好跟蹤參考信號，升降舵偏角處于安全工作范圍，體現了控制器良好的性能，與未考慮平滑切換相比，在工作點切換時刻無控制器輸出跳躍現象.在控制器設計保守性方面，采用文獻［5］的模型，在飛行器工作點區域劃分等初始條件相同的情況下，依定理1計算可得切換多胞系統平均駐留時間下限為2.332 7 s，低于文獻［5］的6.937 8 s，該結果表明定理1具有較低的設計保守性.

4 結論

1)提出一種基于切換多胞系統的高超聲速飛行器魯棒鎮定控制方法.針對飛行器大包線飛行參數時變的鎮定與穩定性分析問題，將高超聲速飛行器包線范圍內的飛行動態建模為切換多胞系統，采用基于參數依賴Lyapunov函數與平均駐留時間方法給出包線范圍漸近穩定的條件，設計了確保多胞系統在參數任意快變下穩定的控制器.

2)仿真結果表明，提出的控制器既能夠保證系統穩定，又克服了切換控制器的控制量跳躍現象，并降低了系統分析與設計的保守性.

［1］RUGH W J，SHAMMA J S.Research on gain scheduling［J］.Automatica，2000，36(10):1401-1425.

［2］HOLLAND S D，WOODS W C，ENGELUND W C.Hyper-X research vehicle experimental aerodynamics test program overview［J］.Journal of Spacecraftand Rockets，2001，38(6):828-835.

［3］談樹萍，李智斌.高超聲速飛行器自適應切換控制及穩定性分析［J］.空間控制技術與應用，2011，37(1):21-27.

［4］張增輝，楊凌宇，申功璋.高超聲速飛行器大包線切換LPV控制方法［J］.航空學報，2012，33(9):1706-1716.

［5］HOU Yanze，WANG Qing，DONG Chaoyang.Gain scheduled control:switched polytopic system approach［J］.Journal of Guidance Control and Dynamics，2011，34(2):623-628.

［6］BOLENDER M A，DOMAN D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle［J］.Journal of Spacecraft and Rockets，2007，44(2):374-387.

［7］HOU Yanze，DONG Chaoyang，WANG Qing.Stability analysis for switched linear systems with locally overlapped switching law［J］.Journal of Guidance Control and Dynamics，2010，33(2):396-403.

［8］PEAUCELLE D，ARZELIER D，BACHELIER O，et al．A new robust d-stability condition for real convex polytopic uncertainty［J］.Systems＆Control Letters.2000，40(1):21-30.

［9］DAAFOUZ J，RIEDINGER P，IUNG C.Stability analysis and control synthesis for switched systems:a switched Lyapunov function approach［J］.IEEE Transactions on Automatic Control，2002，47(11):1883-1887.

［10］TAN Feng，DUAN Guangren，ZHAO Lijun.Robust controller design for autopilot of a BTT missile［C］//Proceedings of the 6th World Congress on Intelligent Control and Automation.Dalian:Dalian Univesity of Technology Press，2006:6358-6362.