一個(gè)不等式的另證及推廣

●鄒生書(shū) (陽(yáng)新縣高級(jí)中學(xué) 湖北陽(yáng)新 435200)

《數(shù)學(xué)通報(bào)》2010年第12期宋慶老師提供的第1 885號(hào)數(shù)學(xué)問(wèn)題如下：

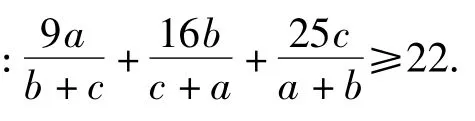
文獻(xiàn)［1］、文獻(xiàn)［2］和文獻(xiàn)［3］對(duì)該不等式給出了證明和推廣.本文給出了一種新的證明，并通過(guò)柯西不等式和判別式法給出不等式的幾種推廣.

且x1+x2+x3=1.故原問(wèn)題可轉(zhuǎn)化為：

推廣1 已知 a，b，c為正數(shù)，且 p，q，r為正常數(shù)，求證：

且x1+x2+x3=1.故原問(wèn)題可轉(zhuǎn)化為：

已知正數(shù) x1，x2，x3滿足 x1+x2+x3=1，求證：

推廣 2 已知 a1，a2，…，an為正數(shù)，且 m1，m2，…，mn為正常數(shù)，n≥3，則

推廣3 已知變量a，b，c為正數(shù)，且λ，μ為正常數(shù)，求證：恒成立.

當(dāng)k=48時(shí)，由式(1)得b≤c恒成立，這與題設(shè)不符，故式(1)恒成立當(dāng)且僅當(dāng)

推廣4 已知變量a，b，c為正數(shù)，且p，q，r為正常數(shù)，求證：

當(dāng)k=4pq時(shí)，由式(2)得(q-p-r)b+(q-r)c≤0，但當(dāng) q-p-r＞0時(shí)此式不成立，因此 k≠4pq，故式(2)恒成立，則當(dāng)且僅當(dāng)k-4pq＜0且

又k≠4pq，所以k-4pq＜0.故式(2)恒成立的充要條件是

根據(jù)推廣4筆者進(jìn)一步提出如下更一般的猜想.

猜想已知變量ai和常數(shù)pi，λi(i∈N，i≥3)均為正數(shù)，則

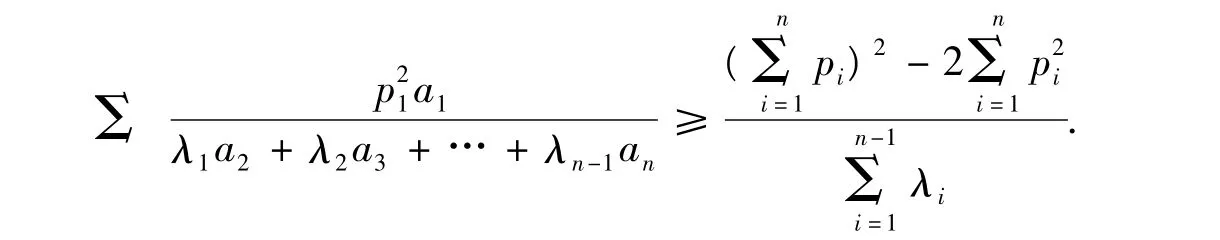
［1］ 宋慶.數(shù)學(xué)問(wèn)題解答［J］.數(shù)學(xué)通報(bào)，2010(12)：59-61.

［2］ 鐘建新.數(shù)學(xué)問(wèn)題1 885的解后再思考［J］.數(shù)學(xué)通報(bào)，2012(3)：50-51.

［3］ 宋志敏，尹櫪.數(shù)學(xué)問(wèn)題1 885的推廣與再研究［J］，數(shù)學(xué)通報(bào)，2011(12)：27-28.