一道解析幾何題運算教學的實踐與思考

●崔志榮 (安豐中學 江蘇東臺 224221) ●薛宗華 (東臺市教育局教研室 江蘇東臺 224221)

注重運算能力的培養(yǎng)，是我國數(shù)學教育“雙基”教學的傳統(tǒng)特色.但是，近年來，學生的運算能力在下降，突出表現(xiàn)在字母運算、處理多元變量等方面，對于高中生而言，解析幾何的運算問題尤為突出.面對這種學習狀況，作為一名高中數(shù)學教師，怎樣在教學中著力提高、逐步培養(yǎng)學生的運算能力呢?

1 一道解析幾何題的考情

最近，筆者所任教學校組織了2013屆高三學生摸底考試，數(shù)學試卷的第19題為：

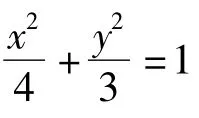
圖1

(1)若l的斜率為1，求l'的方程;

考試結束后，筆者發(fā)現(xiàn)這道解析幾何題并不是特別難，但學生的得分率卻非常低.本題滿分16分，人均得分約6.5分，從具體的統(tǒng)計數(shù)據(jù)來看，大部分學生得到了第(1)小題的6分，只有個別學生答對了第(2)小題.于是筆者又對本班學生進行訪談，大部分學生的回答是“第(2)小題我會做，但時間不夠，來不及運算，如果再給我10分鐘，也許能做對”，還有一部分學生的回答是“這道解析幾何題的第(2)小題計算量太大、太復雜，我沒有信心算下去”.為此，在試卷評講中，筆者側重于對第(2)小題從運算教學的角度作了一些嘗試，現(xiàn)整理成文與大家交流.

2 運算教學的課堂實踐

教師：本題是解析幾何問題，第(2)小題得分率很低，其中一個重要原因是運算能力問題，現(xiàn)在大家都已經(jīng)看到了這道題的參考答案，本節(jié)課我們主要研究第(2)小題的解題運算，哪位同學先來回答一下參考答案的解題思路.

投影展示參考答案(2)設直線AB的方程為

從而線段AB的中垂線方程為

學生1：先聯(lián)立直線與橢圓的方程，化簡得到根與系數(shù)的關系，從而求出弦AB的長與AB中點N的坐標，再由AB的中垂線方程解出點M的橫坐標，可求出弦FM的長，最終得出結論.

教師：不錯，我們把這種方法稱之為“代數(shù)法之韋達定理”.這樣的解題思路容易想到嗎?

學生2：容易想到，但卻不容易解出答案，運算有些復雜.

教師：學生2說運算有些難，難在哪里?

教師：很好，同學們一定要加強運算能力的訓練，只要運算中有一點點失誤，就很難得到正確答案.請同學們再思考，還有沒有別的辦法求弦AB的長，以達到簡化運算的目的.

停頓后有學生回答.

學生4：由于AB是過焦點的弦，因此可用焦點弦長公式|AB|=|e(x1+x2)-2a|.

教師：焦點弦長公式怎么推導?

學生5：運用圓錐曲線的第二定義.

教師：先推導焦點弦長公式，再由此求弦AB的長.

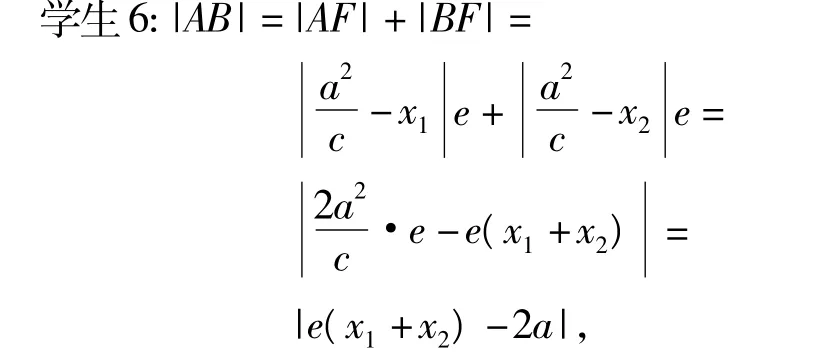
由根與系數(shù)的關系，得

教師：同學們，這樣的解答是不是簡單多了，那么，求弦FM的長有簡化運算嗎?

沒有學生回答.

教師：對于AB中點N的坐標，可用設而不求的辦法嗎?

學生7：設N(x0，y0)，AB 中垂線方程為

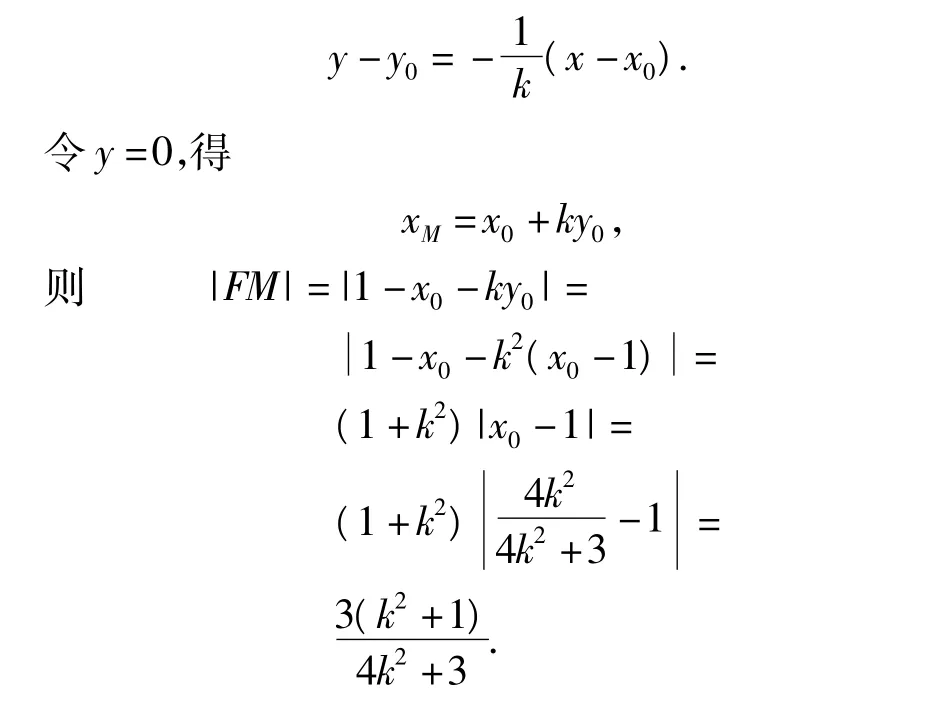
教師：通過優(yōu)化，我們發(fā)現(xiàn)原題的解答運算就不難了，那么是不是參考答案的解答就一無是處呢?

學生8：不是，如果不是焦點弦的問題，那還得按參考答案的方法來求解.

教師：對，我們在處理解析幾何問題時，要加強基本運算的訓練，如果不是焦點弦，那么還得具備一定的運算能力，當然也要總結方法、比較方法，才能有“巧算”.現(xiàn)在，大家重新思考參考答案的解題思路，看是否有其他方法?

學生9：可以用點差法試試，因為涉及到弦的中點問題.

學生 10：設 A(x1，y1)，B(x2，y2)，AB 中點N(x0，y0)，則

教師：同學們用點差法可順利求得AB及AB中垂線的斜率，那么如何求弦AB的長與弦FM的長呢?

教師：學生11仍然運用了焦點弦長公式，得到了弦AB的長只與弦AB中點N的橫坐標有關，那么怎樣求弦FM的長呢?

學生12：AB的中垂線方程為

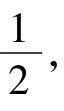
教師：好，下面請同學們來驗證一下老師的猜想對不對.請男生用“代數(shù)法之韋達定理”完成，女生用“代數(shù)法之點差法”完成(目的是加強男生的運算耐心).

教師最后投影展示2組學生代表的解答，并加以點評總結(學生的解答過程與原題的簡化運算基本一致，這里不再書寫了).

教師：通過本節(jié)課的學習，我們在以后的解析幾何學習中有哪些需要注意的地方?

學生14：要加強基本運算能力的訓練，加強方法的比較，通過分析與比較有時會得到“巧算”.

教師：是的，在學習解析幾何時，要重視基本思路、基本運算;要重視分析、比較;要重視過程步驟、針對性訓練.這些問題，在我們以后的學習中，還要進一步加強研究.

3 運算教學的幾點思考

解析幾何作為一種重要的數(shù)學思想方法，一直是高考的重點和熱點之一，這部分內容也格外受到師生的重視.但一個不容否認的事實是：教師往往感到這部分內容的教學效果不如人意，學生似懂非懂，解題出錯率高.結合以上的教學實踐，筆者對解析幾何的教學有幾點思考：

(1)重基本思路，重基礎運算.

本文中測試題的參考答案為基本方法，學生容易理解，教學中不可輕視這種基本思路的講解，但它的運算量偏大，學生不敢動筆，說明基礎運算是我們教學中的一個大問題.在平時教學中，如果過于走捷徑、用技巧運算，會造成學生眼高手低，基礎不扎實，使他們在考場總想容易的方法，那么就容易導致失敗.據(jù)此，筆者認為在解析幾何教學中，要重視基本方法的剖析，淡化技巧方法的講解，淡化特技運算，重視基礎運算.

(2)重分析，重比較.

在解析幾何題中，許多題目是有多種解法的，它們的思路不相同，實際運算效果也不一樣.因此，在教學中要做到：一是重視思路的分析.比如本文中“代數(shù)法之韋達定理”及“代數(shù)法之點差法”都是合理的分析方法.二是重視方法的比較.可以看出，這道題目運用韋達定理與點差法處理的運算效果是不同的，如不涉及到弦的中點，點差法就失效，再如，在韋達定理中，用到了焦點弦長公式，若不是焦點弦，則還需要用參考答案的解法.只有通過思路的分析和比較，才能使不同層次的學生有不同的選擇，才能使他們更準確地認識問題的本質，才能使他們在解題時游刃有余.

(3)重過程步驟，重針對性訓練.

(4)代數(shù)方法為主，幾何方法為輔.

解析幾何的本質是用代數(shù)的方法解決幾何問題.解題結構為：幾何問題到代數(shù)問題到代數(shù)研究再到幾何結果，幾何法不應是解析幾何的教學重點.有些經(jīng)驗豐富的老教師，知道不少解析幾何題的背景，課堂上能把問題一步剖析到簡潔的幾何方法，講得很輕松，又無運算量，學生接受得也快，但實際上卻是無效的，能有多少學生在考場上知道高考題的背景，很快想到巧妙的幾何法?在教學中，還是要腳踏實地用好代數(shù)方法，幾何方法為輔助，比如圓錐曲線的定義、圓的性質等重要的幾何知識可作為輔助使用.

(注：本文是江蘇省鹽城市教育科學“十二五”規(guī)劃課題《提高高中學生運算能力的校本研究》的階段成果.)